• About
• Statistics
• Number Theory
• Java
• Data Structures
• Cornerstones
• Calculus

The Order of an Integer

Provided that $\gcd(b,n) = 1$, Euler's theorem tells us that $b^{k} \equiv 1 \pmod{n}$ is satisfied by $k = \varphi(n)$, but $\varphi(n)$ need not be the smallest positive integer value of $k$ for which this congruence is true.

Consider the following powers of $2 \pmod{7}$:

Note that not only do we have $2^{\varphi(7)} \equiv 2^6 \equiv 1 \pmod{7}$, as we might expect given Euler's theorem - but we also have $2^3 \equiv 1 \pmod{7}$ as well.

Considering powers under a variety of moduli, we see this kind of thing happening with some frequency (as the below tables will show) regardless of whether the modulus is prime or composite.

Given that this is the case, and so that we might have some language with which we might talk about these exponents, let us define the order of $b$ modulo $n$ to be the least positive integer $x$ such that $b^x \equiv 1 \pmod{n}$, and denote this by

As some examples, consulting the tables below, we can see that

Least Positive Residues of $b^x \pmod{19}$



Least Positive Residues of $b^x \pmod{26}$

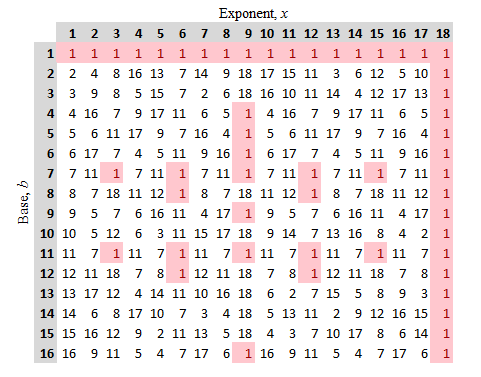
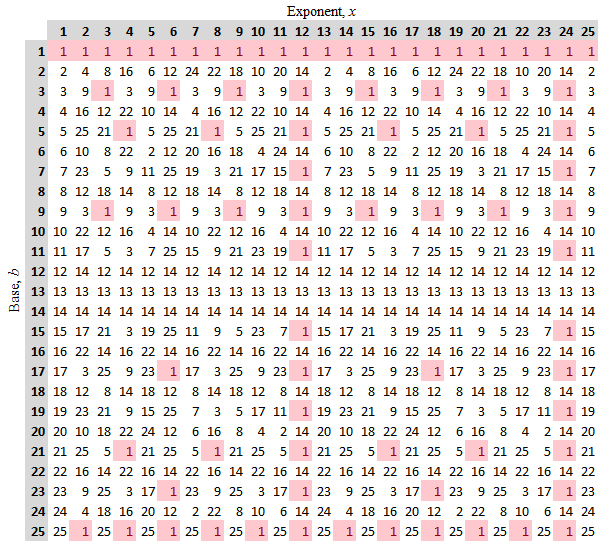
Something else to be noticed in the tables above is that the regular spacing of the pink $1$'s in any given row suggests that

We can prove this rather quickly...

Suppose $\textrm{ord}_n b \mid x$. Then $x = k \cdot \textrm{ord}_n b$, for some positive integer $k$. But then,

On the other hand, suppose $b^x \equiv 1 \pmod{n}$. In this case find the quotient $q$ and remainder $r$ of $x$ upon division by $\textrm{ord}_n b$, so that $$x = q \cdot \textrm{ord}_n b + r$$ In particular, note that we require $0 \le r \lt \textrm{ord}_n b$.

Let us split this into two cases $0 \lt r \lt \textrm{ord}_n b$ and $r=0$, and show the first case leads to a contradiction...

In the first case, if $0 \lt r \lt \textrm{ord}_n b$, then we can argue that

Consequently, since $b^x \equiv 1 \pmod{n}$, it must also be true that $b^r \equiv 1 \pmod{n}$.

This however, in combination with $0 \lt r \lt \textrm{ord}_n b$, would contradict the definition of $\textrm{ord}_n b$, which is required to be the least such positive integer exponent.

The above thus eliminates the possibility that $0 \lt r \lt \textrm{ord}_n b$, leaving us to conclude that the remaining case, $r=0$, must be true.

Of course, knowing that the remainder $r$ upon division of $x$ by $\textrm{ord}_n b$ is zero tells us that $\textrm{ord}_n \mid x$, which is what we hoped to show.

QED.

Note, we may apply this result immediately to that of Euler's theorem to conclude that if $b$ and $n$ are relatively prime integers with $n \gt 0$, then $\textrm{ord}_n b \mid \varphi(n)$.

Lastly - as one more pattern we might notice in the tables above - consider the repeating nature of each row. As can be seen in the selected rows below, the same sequence of least positive residues seems to repeat itself every $\text{ord}_n b$ elements.

Least Positive Residues of $b^x \pmod{26}$

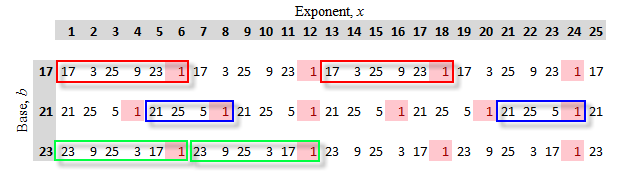
This suggests the following conjecture:

If $b$ and $n$ are relatively prime integers with $n \gt 0$ and $i,j \ge 0$, then

To prove this, consider the following:

Without loss of generality, assume $i \ge j$.

As such, if $i \equiv j \pmod{\text{ord}_n b}$, then we can find some integer $k \ge 0$ such that $i = j + k \cdot \text{ord}_n b$.

But then, knowing $b^{\text{ord}_n b} \equiv 1$ let's us conclude the following:

Conversely, if $b^i \equiv b^j \pmod{n}$, then we can replace the $b^i$ in $b^i \equiv b^j b^{i-j}$ to obtain

We would like to cancel the common $b^j$ on both sides to obtain

This is only allowed if $b^j$ is relatively prime to $n$ -- but recall we presumed $b$ and $n$ were relatively prime integers, which implies that no prime factors of $b$ divide $n$. This in turn tells us that no prime factors of $b^j$ divide $n$, and consequently $b^j$ and $n$ are indeed relatively prime. So the above result is safe to conclude.

Of course now we can use the result we previously proved earlier, namely: $b^x \equiv 1 \pmod{n}$ implies $\textrm{ord}_n b \mid x$, to obtain

or equivalently,

QED.