

 |  |
Verify $\displaystyle{\lim_{x \rightarrow 3} (3x-5) = 4}$ with the epsilon-delta definition of a limit
For any $\epsilon \gt 0$, take $\delta = \epsilon/3 \gt 0$. Then note that whenever $0 \lt |x -3| \lt \delta$,
$$\begin{array}{ll} \implies & |x-3| \lt \epsilon/3\\ \implies & 3|x-3| \lt \epsilon\\ \implies & |3x-9| \lt \epsilon\\ \implies & |(3x-5) - 4| \lt \epsilon \end{array}$$Having shown that for any $\epsilon \gt 0$, we can find a $\delta \gt 0$ so that $|(3x-5) - 4| \lt \epsilon$ whenever $0 \lt |x-3| \lt \delta$, we have satisfied the epsilon-delta definition establishing following limit
$$\displaystyle{\lim_{x \rightarrow 3} (3x-5) = 4}$$What is the behavior of the function $\displaystyle{f(x) = \frac{x-1}{x}}$ as $x \rightarrow 0$ and as $x \rightarrow +\infty$?
That is to say, find the values of the following limits (presuming they exist) and provide a corresponding graphical interpretation:
$$\lim_{x \rightarrow 0} \frac{x-1}{x} \quad \textrm{ and } \quad \lim_{x \rightarrow +\infty} \frac{x-1}{x}$$Note that as $x$ approaches $0$, the numerator gets very close to $-1$, while the denominator gets very small. This means the magnitude of the fraction grows very large (indeed, as $x$ gets close to $0$ the magnitude grows without bound). When $x \lt 0$, the fraction is large and positive. When $x \gt 0$, the fraction is large and negative. In this way, the related left and right limits are determined:
$$\lim_{x \rightarrow 0^-} \frac{x-1}{x} = +\infty \quad \textrm{ and } \quad \lim_{x \rightarrow 0^+} \frac{x-1}{x} = -\infty$$Of course, as these left and right limits disagree, we conclude $\displaystyle{\lim_{x \rightarrow 0} \frac{x-1}{x}}$ does not exist.
(Technically, whenever a limit is infinite, it fails to exist - but the disagreement between the left and right limiting values is in a sense even more important here.)
Graphically, since at least one of the left or right limits associated with $x = 0$ is infinite, there is a vertical asymptote in the associated graph at this $x$ value.
As $x$ approaches $+\infty$, something different happens. Note that the relative difference between the numerator and denominator becomes smaller and smaller, allowing the overall fraction to become arbitrarily close to $1$. This is the value of the related limit.
There is another way to see this, however. Suppose we divide both the numerator and denominator by $x$. This does not change the value of the expression unless $x=0$, but the limiting value (presuming it exists) does not care what the function actually does at $0$.
$$\lim_{x \rightarrow +\infty} \frac{x-1}{x} = \lim_{x \rightarrow +\infty} \frac{1 - 1/x}{1} = 1$$Note how in the result, as $x$ gets larger and larger, the term $1/x$ gets smaller and smaller (i.e., it has a limiting value of $0$) -- effectively vanishing as $x \rightarrow +\infty$. This leaves a limiting value of $1$ associated with the rest of the expression.
Graphically, as there was limiting value associated with $x \rightarrow +\infty$, the associated graph has a horizontal asymptote of $y=1$.
Examine the behavior of $\displaystyle{h(x) = \left\{ \begin{array}{rl} x^2, & x \ne 2\\ 3, & x = 2 \end{array} \right.}$ as $x \rightarrow 2$.
That is to say, find the value of $\displaystyle{\lim_{x \rightarrow 2} h(x)}$ presuming it exists, and provide a corresponding graphical interpretation.
As $h(x)$ only disagrees with $x^2$ when $x = 2$, the value we seek must equal $\lim_{x \rightarrow 2} x^2$. The limit laws quickly establish this value to be $4$.
Graphically, as $h(2)$ exists but does not agree with $\lim_{x \rightarrow 2} h(x)$, we have an isolated point at $(2,3)$ in the graph.
Examine the behavior of $f(x) = \sin x$ as $x \rightarrow +\infty$.
As $x$ continues to increase, $\sin x$ simply oscilates back and forth between a minimum value of $-1$ and a maximum value of $1$. As it never stays arbitrarily close to any height for sufficiently large $x$, $\displaystyle{\lim_{x \rightarrow +\infty} \sin x}$ fails to exist.
Evaluate the following limits and provide corresponding graphical interpretations for each:
$$(\textrm{a}) \lim_{t \rightarrow 2} t \quad (\textrm{b}) \lim_{s \rightarrow -\infty} \frac{1}{s} \quad (\textrm{c}) \lim_{z \rightarrow 0^+} \frac{-1}{z}$$(a) $2$; (b) $0$; (c) $-\infty$
Let $\displaystyle{f(x) = \left\{ \begin{array}{rl} x \cos \pi x, & x \lt 1\\ 2, & x = 1\\ x^2, & x \gt 1 \end{array} \right.}$
Find the following limits:
$$(\textrm{a}) \lim_{h \rightarrow 0^+} f(1+h) \quad (\textrm{b}) \lim_{h \rightarrow 0^+} f(1-h) \quad (\textrm{c}) \lim_{h \rightarrow 0^-} f(1+h) \quad (\textrm{d}) \lim_{h \rightarrow 0^-} f(2+h)$$(a) $1$; (b) $-1$; (c) $-1$; (d) $4$
Find the slope of the secant line of $f(x) = \sqrt{x}$ through the points $(4,f(4))$ and $(4+h,f(4+h))$. Find the limiting slope of the secant line as $h \rightarrow 0$; use this to find an equation of the tangent line to the graph of $f$ at $x=4$.
Slope of secant line: $\displaystyle{m = \frac{1}{2 + \sqrt{4+h}}}$; equation of tangent line (e.g.): $\displaystyle{y - 2 = \frac{1}{4}(x-4)}$
Compute $\displaystyle{\lim_{x \rightarrow -2} \frac{2x}{x^2-2}}$ citing appropriate limit laws that justify each step.
We have a limit of a quotient, which if the denominator's limiting value is non-zero, can be found as the quotient of the limiting values of the numerator and denominator.
Thus, we look at the limit of the denominator:
$$\lim_{x \rightarrow -2} (x^2 - 2)$$As $x^2-2$ is a polynomial and $\displaystyle{\lim_{x \rightarrow c} p(x) = p(c)}$ for any polynomial function $p(x)$, we have the limit of the denominator being $2^2 - 2 = 2$.
The limit of the numerator is similarly $2(-2) = -4$, as it too is a polynomial function whose limit can be found by direct evaluation.
Thus,
$\displaystyle{\lim_{x \rightarrow -2} \frac{2x}{x^2-2} = \frac{-4}{2} = -2}$Evaluate and provide a graphical interpretation: $\displaystyle{\lim_{x \rightarrow 2} \frac{x-2}{x^2-4}}$
Note that the limiting values of the numerator and denominator as $x \rightarrow 2$ are both $0$. However, there is a common factor of $(x-2)$ that can be cancelled that doesn't effect the value of the limit:
$$\begin{array}{rcl} \displaystyle{\lim_{x \rightarrow 2} \frac{x-2}{x^2-4}} &=& \displaystyle{\lim_{x \rightarrow 2} \frac{x-2}{(x-2)(x+2)}}\\ &=& \displaystyle{\lim_{x \rightarrow 2} \frac{1}{(x+2)}} \end{array}$$At this point, we have the limit of a rational expression with $x$ approaches a value that is not a domain issue. By one of the limit laws, we can thus evaluate the limit by simply evaluating the function at $x=2$ to determine
$$\displaystyle{\lim_{x \rightarrow 2} \frac{1}{(x+2)} = \frac{1}{2+2} = \frac{1}{4}}$$Graphically, as the original expression had a domain issue but the limit existed, we have a hole at $(2,1/4)$.
Evaluate and provide a graphical interpretation: $\displaystyle{\lim_{x \rightarrow -3} \frac{-2 + \sqrt{7+x}}{x+3}}$
The limiting values of the numerator and denominator as $x \rightarrow -3$ are both $0$. Fortunately, multiplying by a well-chosen value of one by using the conjugate of the numberator will reveal a common factor that can be cancelled that doesn't effect the value of the limit.
This technique is called rationalizing the numerator.
$$\begin{array}{rcl} \displaystyle{\lim_{x \rightarrow -3} \frac{-2 + \sqrt{7+x}}{x+3}} &=& \displaystyle{\lim_{x \rightarrow -3} \frac{-2 + \sqrt{7+x}}{x+3} \cdot \frac{-2 - \sqrt{7+x}}{-2 - \sqrt{7+x}}}\\ &=& \displaystyle{\lim_{x \rightarrow -3} \frac{4 - (7+x)}{(x+3)(-2 - \sqrt{7+x})}}\\ &=& \displaystyle{\lim_{x \rightarrow -3} \frac{-(x+3)}{(x+3)(-2 - \sqrt{7+x})}}\\ &=& \displaystyle{\lim_{x \rightarrow -3} \frac{1}{2 + \sqrt{7+x}}}\\ \end{array}$$At this point, since the limit of both the numerator and denominator as $x \rightarrow -3$ are both not zero, the overall limit can be found simply by evaluating the last expression at $x=-3$ to obtain
$$\displaystyle{\lim_{x \rightarrow -3} \frac{1}{2 + \sqrt{7+x}} = \frac{1}{2 + \sqrt{7-3}} = \frac{1}{4}}$$Noting that there was a domain issue in the expression for $x=-3$ but the limit ultimately existed, tells us that graphically one has a hole at $(-3,1/4)$ in the corresponding graph.
Evaluate and provide a graphical interpretation: $\displaystyle{\lim_{x \rightarrow -1} \frac{|x+1|}{x+1}}$
First, we note the limiting values of the numerator and denominator as $x \rightarrow -1$ are both $0$, so we can't find the limit (presuming it exists) by direct evaluation.
The presence of the absolute value function is really a piecewise-defined function in disguise. To see this, note
$$|x| = \left\{ \begin{array}{rl} x, & x \ge 0\\ -x, & x \lt 0 \end{array} \right.$$As the "border" between the two "pieces" in $|x+1|$ is at $x=-1$, the very value we approach in the limit -- we will want to find the related left and right limits separately, lest they disagree and cause the overall limit to not exist:
$$\lim_{x \rightarrow -1^-} \frac{|x+1|}{x+1} = \lim_{x \rightarrow -1^-} \frac{-(x+1)}{x+1} = \lim_{x \rightarrow -1^-} {-1} = -1$$ $$\lim_{x \rightarrow -1^+} \frac{|x+1|}{x+1} = \lim_{x \rightarrow -1^+} \frac{(x+1)}{x+1} = \lim_{x \rightarrow -1^+} {1} = 1$$As can be seen, the corresponding left and right limits exist, but disagree in value.
Thus, $\displaystyle{\lim_{x \rightarrow -1} \frac{|x+1|}{x+1}}$ does not exist.
Graphically, as the left and right limiting values existed but disagreed, we have a gap (or jump) discontinuity in the corresponding graph from $(-1,-1)$ to $(-1,1)$.
Evaluate and provide a graphical interpretation: $\displaystyle{\lim_{x \rightarrow 0} \sin \left( \frac{1}{x} \right)}$.
As $x$ approaches $0$, note that $1/x$ grows very large (without bound) in magnitude. Taking the sine of larger and larger values results in values that oscillate back and forth between $-1$ and $1$. Thus, $\sin (1/x)$ never stays arbitrarily close to any value as $x$ stays sufficiently close to $0$ (ignoring $x=0$ itself). So this limit does not exist due graphically to infinite, non-damped oscillitory behavior.
Evaluate and provide a graphical interpretation: $\displaystyle{\lim_{x \rightarrow 0} x^2 \sin \left( \frac{1}{x} \right)}$.
In this case, we see $\sin (1/x)$ oscillates between $-1$ and $1$ as $x \rightarrow 0$, but this oscillation is damped by the $x^2$ factor. Indeed, we can bound $x^2 \sin (1/x)$ between two simple functions:
$$-x^2 \le x^2 \sin \left(\frac{1}{x}\right) \le x^2$$As the limiting values of both $-x^2$ and $x^2$ are $0$ as $x \rightarrow 0$, the limiting value of $x^2 \sin (1/x)$ as $x \rightarrow 0$ must also be $0$, by the Squeeze Theorem.
Graphically, since $x=0$ is a domain issue in the original expression, but the limit value existed, we have a hole in the corresponding graph. In this case, that hole is at $(0,0)$.
Evaluate and provide a graphical interpretation: $\displaystyle{\lim_{x \rightarrow +\infty} \frac{x^2 + 4x}{x^2 + 4}}$.
Note as $x \rightarrow +\infty$ both the numerator and denominator get large (without bound).
To reveal the nature of the overall fraction as $x \rightarrow +\infty$, however, let us divide both top and bottom by the highest power of $x$ seen in the denominator (namely, $x^2$). This reveals terms $4/x$ and $4/x^2$ which vanish as $x \rightarrow +\infty$, making the resolution of the rest of the limit simple:
$$\lim_{x \rightarrow +\infty} \frac{x^2 + 4x}{x^2 + 4} = \lim_{x \rightarrow +\infty} \frac{1 + 4/x}{1 + 4/x^2} = \lim_{x \rightarrow +\infty} \frac{1}{1} = 1$$Graphically, as the limit at infinity existed, there is a horizontal asymptote in the corresponding graph. In this case, we have a horizontal asymptote of $y = 1$.
Compute $\displaystyle{\lim_{x \rightarrow -1} (x^4 - 3x)(x^2 + 5x + 3)}$, justifying each step with an appropriate limit law.
We can work this problem out in a couple of ways. Let's first work this out the "long way", which will let us see several different limit laws at work.
The "Long Way":
$$\begin{array}{rclr} & & \displaystyle{\lim_{x \rightarrow -1} (x^4 - 3x)(x^2 + 5x + 3)} &\\ &=& \displaystyle{\left( \lim_{x \rightarrow -1} (x^4 - 3x) \right) \left( \lim_{x \rightarrow -1} (x^2 + 5x + 3) \right)} & \textrm{(limit of a product)}\\ &=& \displaystyle{\left( \lim_{x \rightarrow -1} x^4 - \lim_{x \rightarrow -1} 3x \right) \left( \lim_{x \rightarrow -1} (x^2 + 5x + 3) \right)} & \textrm{(limit of a difference)}\\ &=& \displaystyle{\left( \lim_{x \rightarrow -1} x^4 - \lim_{x \rightarrow -1} 3x \right) \left( \lim_{x \rightarrow -1} x^2 + \lim_{x \rightarrow -1} 5x + \lim_{x \rightarrow -1} 3 \right)} & \textrm{(limit of a sum)}\\ &=& \displaystyle{\left( \lim_{x \rightarrow -1} x^4 - 3 \cdot \lim_{x \rightarrow -1} x \right) \left( \lim_{x \rightarrow -1} x^2 + 5 \cdot \lim_{x \rightarrow -1} x + \lim_{x \rightarrow -1} 3 \right)} & \textrm{(scalar multiple rule)}\\ &=& \displaystyle{\left( \lim_{x \rightarrow -1} x^4 - 3 \cdot \lim_{x \rightarrow -1} x \right) \left( \lim_{x \rightarrow -1} x^2 + 5 \cdot \lim_{x \rightarrow -1} x + 3 \right)} & \textrm{(constant rule)}\\ &=& \displaystyle{\left( \left( \lim_{x \rightarrow -1} x\right)^4 - 3 \cdot \lim_{x \rightarrow -1} x \right) \left( \left(\lim_{x \rightarrow -1} x\right)^2 + 5 \cdot \lim_{x \rightarrow -1} x + 3 \right)} & \textrm{(power rule)}\\ &=& \displaystyle{\left((-1)^4 - 3 \cdot(-1)\right) \left((-1)^2 + 5 \cdot (-1) + 3\right)} & \textrm{(limit of identity function)}\\ &=& -4 & \end{array}$$Now, let's work the same problem in a much shorter way by choosing more powerful limit laws to employ.
The "Short Way"
$$\begin{array}{rclr} & & \displaystyle{\lim_{x \rightarrow -1} (x^4 - 3x)(x^2 + 5x + 3)} &\\ &=& \displaystyle{\left( \lim_{x \rightarrow -1} (x^4 - 3x) \right) \left( \lim_{x \rightarrow -1} (x^2 + 5x + 3) \right)} & \textrm{(limit of a product)}\\ &=& \displaystyle{\left((-1)^4 - 3 \cdot(-1)\right) \left((-1)^2 + 5 \cdot (-1) + 3\right)} & \textrm{(limit of a polynomial)}\\ &=& -4 & \end{array}$$Evaluating the limit minimally requires applying the rules for the limit of a quotient and limit of polynomial (although could alternatively use the limit of a sum, difference, quotient, and scalar multiple), and results in $7/8$.
Find the slope of the tangent line at $x = -4$ to $f(x) = \sqrt{1-2x}$ by computing the limit $\displaystyle{\lim_{x \rightarrow -4} \frac{f(x) - f(-4)}{x+4}}$. Then find an equation for this tangent line.
The slope is $-1/3$ and computed by rationalizing the numerator. The tangent line has equation $\displaystyle{y-3 = -\frac{1}{3}(x+4)}$
Find an equation for the tangent line to $f(x) = 1-2x^2$ at $x = -1$.
$y+1 = 4(x+1)$
Suppose that $2x \le f(x) \le x^4 - x^2 + 2$ for all $x \ge 0$. Compute $\displaystyle{\lim_{x \rightarrow 1} f(x)}$.
Since $\displaystyle{\lim_{x \rightarrow 1} 2x = 2 = \lim_{x \rightarrow 1} (x^4 - x^2 + 2)}$, by the squeeze theorem, $\displaystyle{\lim_{x \rightarrow 1} f(x) = 2}$ as well.
(Challenge!) What is the behavior of the function $\displaystyle{g(x) = \frac{\sin x}{x}}$ as $x \rightarrow 0$ and as $x \rightarrow +\infty$?
That is to say, find the values of the following limits (presuming they exist) and provide a corresponding graphical interpretation. Justify your conclusions with a logical argument.
$$\lim_{x \rightarrow 0} \frac{\sin x}{x} \quad \textrm{ and } \quad \lim_{x \rightarrow +\infty} \frac{\sin x}{x}$$While estimating the value of $\displaystyle{\frac{\sin x}{x}}$ with small values of $x$ (as was done earlier in the notes) suggests a limiting value of $1$, proving this is the actual limiting value takes some creativity.
Consider the following image:
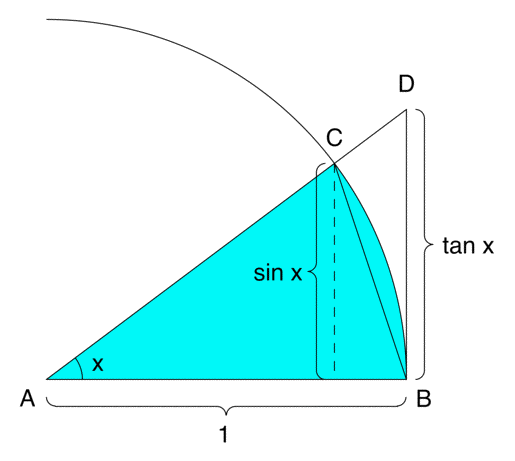
Note that the area of $\triangle ABC$ is $\displaystyle{\frac{\sin x}{2}}$, the area of the teal-shaded wedge is $\displaystyle{\frac{x}{2}}$, and the area of $\triangle ABD$ is $\displaystyle{\frac{\tan x}{2}}$.
As $\triangle ABD$ contains the wedge, which in turn contains $\triangle ABC$, we have the following inequality:
$$\frac{\tan x}{2} \ge \frac{x}{2} \ge \frac{\sin x}{2}$$Dividing everything above by $\displaystyle{\frac{\sin x}{2}}$ and taking reciprocals, we get
$$\cos x \le \frac{\sin x}{x} \le 1$$Note that since $\displaystyle{\frac{\sin x}{x}}$ and $\cos x$ are both even functions, the inequality immediately above is valid for any non-zero $x$ between $-\pi/2$ and $\pi/2$.
Finally, we can appeal to the Squeeze Theorem. Note the limiting values of $\cos x$ and $1$ as $x \rightarrow 0$ are both $1$. Thus, the expression $\displaystyle{\frac{\sin x}{x}}$ bound between them must have a limiting value of $1$ when $x \rightarrow 0$ as well. As such,
$$\lim_{x \rightarrow 0} \frac{\sin x}{x} = 1$$Graphically, as $\sin x / x$ is undefined when $x=0$ but the limit exists there, we have a hole in the associated graph at $(0,1)$.
The second limit, where $x \rightarrow +\infty$, can be found more quickly -- again using the Squeeze Theorem. Note that we can bound $\displaystyle{\frac{\sin x}{x}}$ above and below with the following two functions.
$$\frac{-1}{x} \lt \frac{\sin x}{x} \lt \frac{1}{x}$$As both $-1/x$ and $1/x$ have a limiting value of $0$ as $x \rightarrow +\infty$, it must be the case that $\displaystyle{\frac{\sin x}{x}}$ does as well. Thus,
$$\lim_{x \rightarrow +\infty} \frac{\sin x}{x} = 0$$Graphically, as the limit at infinity existed, the associated graph has a horizontal asymptote whose height matches the value of the limit (i.e., $y = 0$).
As a curious final note -- unlike horizontal asymptotes in many other graphs, the oscillatory nature of the sine function here causes an infinite number of intersections between our function and the asymptote.