The Intermediate Value Theorem

Let's set the stage for talking about this very important theorem by considering the following thought experiment:

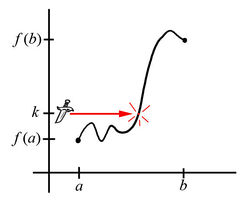
Suppose you graph some function $f(x)$ that is continuous on the closed interval $[a,b]$. Recall that at $x=a$ our function must be $f(a)$ high, and likewise at $x=b$, the function must be $f(b)$ high. Consequently, you can think of this function as a continuous piece of string anchored at $(a,f(a))$ and $(b,f(b))$.

Now suppose you have a knife at height $k$, which falls strictly between $f(a)$ and $f(b)$. If we slash the knife at this height across the entire interval from $a$ to $b$, what will happen to our string?

Fig. 1

Fig. 2

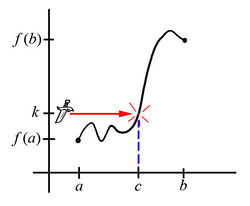Of course, the string must get cut at some point. Further, the $x$-coordinate of the point where it gets cut must fall somewhere strictly between $a$ and $b$, say at some $x=c$.

Equivalently, there must be some value $c$ in the interval $(a,b)$ where $f(c)=k$.

This hopefully makes good intuitive sense, and suggests the following theorem:

The Intermediate Value Theorem

If $f(x)$ is a function such that

$f(x)$ is continuous on the closed interval $[a,b]$, and
$k$ is some height strictly between $f(a)$ and $f(b)$. In other words, either $f(a) \lt k \lt f(b)$ or $f(b) \lt k \lt f(a)$

Then, there is some value $c$ in the interval $(a,b)$ where $f(c)=k$.

One should realize, however, that our thought experiment with the knife does not prove this implication holds whenever $f(x)$ is continuous over $(a,b)$ and $k$ lies between $f(a)$ and $f(b)$. To do that, we will need to appeal to the epsilon-delta definition of a limit and the definition of continuity.

Putting that off for the moment, though, one should also notice what this theorem (once it is proven) does not tell us:

First, the Intermediate Value Theorem does not forbid the occurrence of such a $c$ value when either $f(x)$ is not continuous or when $k$ does not fall between $f(a)$ and $f(b)$.

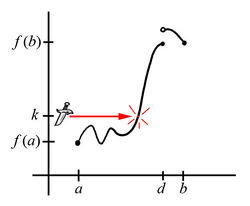
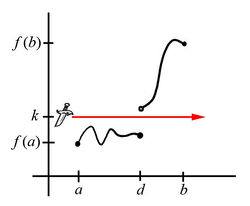
So, if our function has any discontinuities (consider $x=d$ in the graphs below), it could be that this $c$-value exists (Fig. 3) or it might not (Fig. 4). The Intermediate Value Theorem does not apply here. It simply has nothing to say about the graph of $f(x)$ in this situation.

Fig. 3

Fig. 4

Likewise, if the value of $k$ fails to be strictly between $f(a)$ and $f(b)$, it could be that this $c$-value exists (Fig. 5) or it might not (Fig. 6). Again, the Intermediate Value Theorem does not apply here -- and consequently does not require $f(x)$ to behave in any particular way.

Fig. 5

Fig. 6

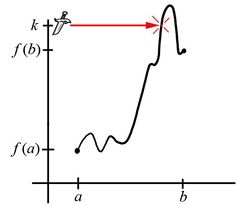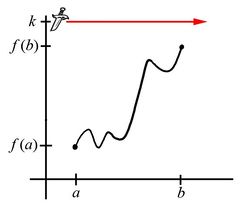Second, the Intermediate Value Theorem -- even when it does apply -- does not tell us anything about which value of $c$ in $(a,b)$ makes $f(c)=k$. It only guarantees the existence of such a value $c$ in this interval!

Now, it is true that we might be able to find a value for $c$ by solving the equation $f(x)=k$ and determining which of the solutions found fall inside the interval $(a,b)$, although we can just as easily discover that $f(x)$ is so complicated that finding exact solutions to $f(x)=k$ is impossible.