

 |  |
We have said before that we can think of a limit as an "expected" value for a function at some given $x=c$ when the actual behavior there is hidden from us.
In forming that expectation, we assume the graph of the function can be drawn near that point with a single continuous stroke of the pen. This assumption lies at the heart of how we can quickly approximate limiting values for a function given its graph.
However, we can't rigorously define what we mean by a limit in this way. Doing so would be entirely too subjective!
What we need is a clear, precise, and unambiguous definition for a limit that is consistent with the intuitive notion we have developed.
Too often, if you ask someone who has had a brief exposure to Calculus what a limit is, they will tell you (incorrectly) that the limit of a function at some value $c$ is defined as the value that $f(x)$ approaches as $x$ approaches $c$.
After a moment's thought, however, you should realize this would actually be a terrible definition -- one that is not at all consistent with our notion of a limit as an "expected height or value".
Consider the following two functions:
|
Graph A 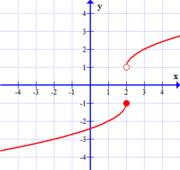 $$y=f(x)$$ |
Graph B 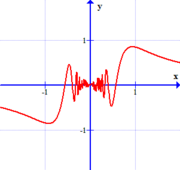 $$y=g(x)$$ |
|
In graph $A$ above -- if we use this bad definition -- we are forced to accept that $\lim_{x \rightarrow 2} \,\, f(x) = 0$. After all, as $x$ approaches $2$ from either side, the height of the function approaches $0$. Indeed, one could argue that the limiting value must also be 1/2, -1/3, and a multitude of other values too! Clearly there is a problem here. Intuitively, knowing that we have a gap, or jump discontinuity at $x=2$, we should have two different, and conflicting "expectations" for the value of $f(2)$ when the actual behavior there is hidden from us. With no reason to pick one over the other, and hence no single "expected value", this limit should not even exist! |
In graph $B$ above, on the other hand, shows us the reverse situation -- even when the $x$-values considered are very close to $0$ -- there are always times when $f(x)$ is moving farther away from a height of zero as $x$ approaches zero. Thus, if we use this bad definition, we are forced to conclude that $\lim_{x \rightarrow 0} g(x) \neq 0$. However, given the damped amplitude of the function around $x=0$, our intuition tells us to "expect" $f(0)=0$, so the limit really should exist. |
Think carefully about both of the cases above. Do you see why what is being said is true?
So the question now is: "How do we fix what went wrong in the above attempt to better define the notion of limit?"
Notice, in graph $A$, $f(x)$ never gets any closer than one unit away from its (incorrectly) stated limiting height of zero. With our intuitive notion of a limit, we really need to be able to get arbitrarily close to the limiting height.
Also, in graph $B$, the direction $f(x)$ is heading (i.e., either approaching or getting farther away from the limiting height) shouldn't matter near as much as the fact that we can keep $f(x)$ close to the limiting height, provided the $x$-values we consider are sufficiently close to the $c$-value in question.
Putting these two ideas together with the fact that we really don't care what happens to $f(x)$ at $x=c$ gives us a working definition:
$\lim_{x \rightarrow c} \,\, f(x)=L$ means that we can keep $f(x)$ arbitrarily close to $L$, by keeping $x$ sufficiently close to $c$, with the possible exception of what happens at $x=c$. |
This is a good definition, but is it the most useful? How can one, for instance, use this to verify a limit's value? To cite a particular example, how would you show -- using the above definition -- that $\lim_{x \rightarrow 2} \,\, x^2 = 4$ ?
The following definition, while perhaps a bit harder to follow, is completely equivalent to the one above, and -- believe it or not -- is actually easier to work with when trying to verify the value of a limit.
$\lim_{x \rightarrow c} \,\, f(x)=L$ means that for any $\epsilon>0$, we can find a $\delta>0$ such that if $0<|x-c|<\delta$, then $|f(x)-L| < \epsilon$. |
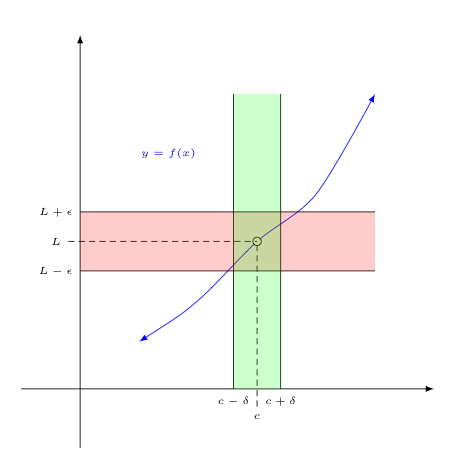
To see the equivalence of the two definitions given, a few comments are in order:
First, $\epsilon$ provides us with a measure of how "arbitrarily close" to $L$ we wish $f(x)$ to be. In the context of the picture above, $\epsilon$ determines the height of the "red band" about $L$.
Notice that $|f(x)-L|$ is the distance between the height of the function at some $x$ and the height $L$. So, $|f(x)-L| < \epsilon$ tells us that the height of $f(x)$ is staying within $\epsilon$ units of a height of $L$.
In other words, when $|f(x) - L| < \epsilon$ holds, the value of $f(x)$ is being kept in the desired $\epsilon$-band about $L$.
Second, $\delta$ provides us with a measure of how "sufficiently close" to $c$ we must keep $x$. In the context of the picture above, $\delta$ determines the width of the "green band" about $c$.
Notice that $|x-c|$ is the distance between $x$ and $c$. So, $|x-c|<\delta$ tells us that $x$ is staying within $\delta$ units of $c$.
So $|x-c| < \delta$ tells us that we have chosen an $x$ in the green $\delta$-band.
We require $\epsilon > 0$ as:
distances must never be negative; and
We require $\delta > 0$ for similar reasons:
$\delta$ also represents a distance, so it can't be negative; and
$\delta$ can't be zero, as then the only $x$ value we would be considering would be $c$ itself, which is precisely the value of $x$ we don't care about!
Finally, we restrict our conclusions to $0 < |x - c|$ to purposefully avoid placing any restrictions on what happens at $x=c$. Remember, in the first definition, what happens there is a "possible exception".