• About
• Statistics
• Number Theory
• Java
• Data Structures
• Cornerstones
• Calculus

Concavity

Imagine you are riding a motorcycle at a dangerously fast speed on a race track. Upon striking a rock, the bolt that keeps the front tire on your bike sadly snaps, bringing your bike to an immediate stop. However, thanks to Newton's first law of motion, you continue to move forward -- flying over the handle-bars and landing a few feet in front of your bike.

Of course, the direction you fly follows the tangent to the path that was being traversed by the bike at the spot where the accident occurred.

Consider if the race track had been curving to the left when this happened -- wouldn't you always be thrown to the right side of the track? If the race track had been curving to the right when this happened, wouldn't you have been thrown to the left side of the track?

In a similar way, think of a particle traveling along some differentiable function in the coordinate plane. Note how any tangent line to the function at a place where the function "curves upward" should stay below the function (at least near the point of tangency). However, tangents drawn to points where the function "curves downward" instead stay above the function.

We make these ideas concrete with the following definitions:

For a function $f$ that is differentiable at $c$, we say

• $f$ is concave up at $c$ means that $f(x)$ lies above the tangent line to $f$ at $x=c$, for all $x \ne c$ sufficiently near $c$.
• $f$ is concave down at $c$ means that $f(x)$ lies below the tangent line to $f$ at $x=c$, for all $x \ne c$ sufficiently near $c$.

Similarly, if $f$ is a function whose domain contains the interval $I$, and $f$ is differentiable on $I$, we say $f$ is concave up on $I$ if $f$ is concave up at every $x$ in $I$, and concave down on $I$ if $f$ is concave down at every $x$ in $I$.

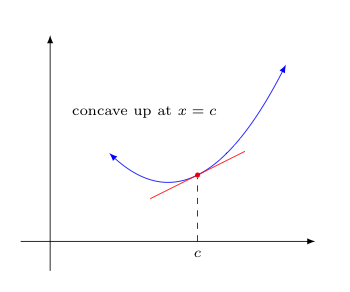
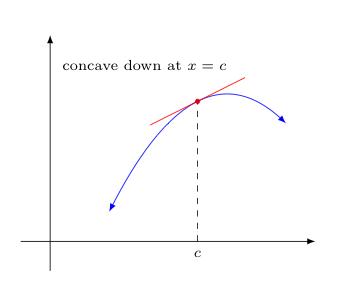
Additionally, we define as points of inflection those special points where the concavity of a function changes from concave up to concave down or vice-versa.

Being able to determine the above-described concavity (up or down) of a function on various intervals and to locate a function's points of inflection will help us in a substantial way in understanding the nature of the graph of that function.

Fortunately, there is a simple connection between the concavity of a function and its second-derivative:

To convince the curious among you of this, let us prove the first part of the theorem above:

Recall, $\displaystyle{\lim_{x \rightarrow c} \frac{f'(x) - f'(c)}{x-c} = f''(c)}$. Thus, as $f''(c) \gt 0$, the limit at left must be greater than zero as well.

Consider the consequences in terms of the epsilon-delta definition for this limit when we pick $\epsilon = f''(c)/2$.

Notably, this value of epsilon is a distance shorter than the distance between $f''(c)$ and $0$. It must then be the case that there is an open ($\delta$-band) interval $I$ containing $c$ such that $$\quad \quad \quad \frac{f'(x) - f'(c)}{x-c} \gt 0 \quad \textrm{ for every } x \ne c \textrm{ in } I \quad \quad \quad (*)$$

Now consider the tangent line to $f$ at $x=c$, whose equation is given by

For any $x \ne c$ in $I$, we hope to show that $f(x) \gt L(x)$, which would mean that $f(x)$ lies above the tangent line to $f$ at $x=c$ for all $x \ne c$ sufficiently near $c$. This would give us the desired result -- that $f$ is concave up at $c$.

Equivalently, upon replacing $L(x)$ with its formula above, we hope to show

Distributing the negative and rearranging terms, we see we only need to show $$\left[f(x) - f(c)\right] - f'(c)(x-c) \gt 0$$

Notice the mean-value theorem applies here and concludes there is a $d$ strictly between $x$ and $c$ where

This in turn tells us that $f(x) - f(c) = f'(d)(x-c)$.

Combining this with our earlier result, we need only show

or equivalently,

Our intention is to do this by showing these two factors have the same signs.

Notice that $d$ is in $I$, so by $(*)$ above we have

• Case 1: If $x - c \gt 0$, then $x \gt c$. As $d$ is strictly between $x$ and $c$, we must then also have $d \gt c$. But then, by the inequality directly above, $f'(d) - f'(c) \gt 0$. So $(x-c)$ and $(f'(d)-f'(c))$ have the same sign.

• Case 2: If $x - c \lt 0$, then $x \lt c$. As $d$ is strictly between $x$ and $c$, we must then also have $d \lt c$. But then, by the inequality directly above, $f'(d) - f'(c) \lt 0$. So $(x-c)$ and $(f'(d)-f'(c))$ have the same sign.

So in either case, the two factors $(x-c)$ and $(f'(d)-f'(c))$ have the same sign -- which is what we needed to show.