

 |  |
We saw when we introduced complex numbers previously that multiplication of one complex number by another involves both rotation about the origin and scaling the distance from the same. Of course, if the complex numbers involved were both of unit magnitude, then only rotation was involved.
With this in mind, let us consider again the unit circle of complex values with unit magnitude. In particular, let us consider the real and imaginary parts of the $z$ on that unit circle where $\theta = arg(z)$ is known. We should recognize that knowing $\theta$ fixes exactly where this $z$ must be located in the complex plane. To see this, imagine one starts at $0$ (the origin) and then moves exactly one unit distance in a direction corresponding to $\theta$.
The real part of such a $z$ and its imaginary coefficient (and consequently the $x$ and $y$ coordinates of the corresponding point in the related coordinate plane -- also called the Cartesian plane, named after French mathematician Rene Descartes.) are also then fixed once we know $\theta$. In this way, we can think of these $x$ and $y$ coordinates as functions of $\theta$. To attach specific names to these functions, let us make the following definitions.
(...and don't worry, we'll explain exactly why we name them with these two specific names very soon!)
|
For any $\theta$, let $z = x + iy$ be the unique complex value on the unit circle (i.e., $|z| = 1$) with argument $\theta$. Then, define functions cosine and sine, denoted* $\cos \theta$ and $\sin \theta $ respectively, so that: $$\cos \theta = x = Re(z) \quad \textrm{ and } \quad \sin \theta = y = Im(z)$$ *Note that -- just like log functions -- we traditionally omit the parentheses around the input when doing so doesn't cause confusion. |
As an ink-saving way to refer to the unique $z$ on the unit circle with a given argument $\theta$, we might find it useful to also define the following suggestively-named function:
|
Let $\textrm{cis}(\theta)$ be defined to be the unique complex value on the unit circle with argument $\theta$, which then requires $$\textrm{cis}(\theta) = \cos(\theta) + i \sin(\theta)$$ |
To visualize what these functions do, consider the diagram drawn on the left below. Of course, we can also (and more frequently do) draw such things instead on the related coordinate plane, as shown on the below right.
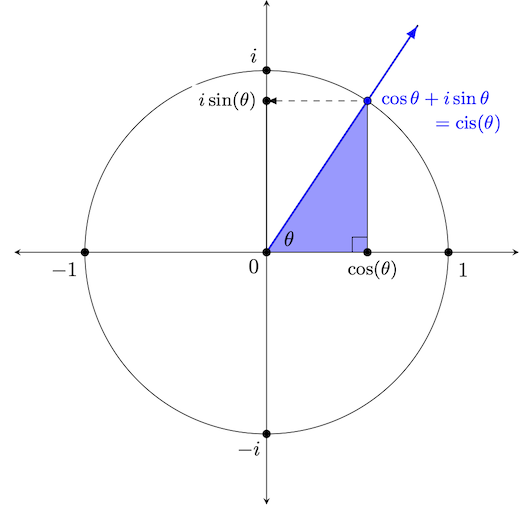
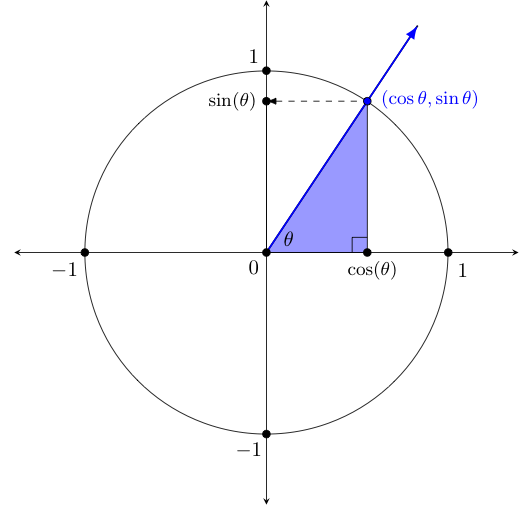
You may be curious about why we have included the shaded blue triangle in the diagram as well. This triangle -- formed by drawing a vertical line from the point on the unit circle to the real axis (or $x$-axis on the right) is called a reference triangle, and serves as a way to quickly compute sine and cosine values for certain commonly encountered angles. We will have more to say about it shortly.
For now, let us simply say that the cosine and sine functions form the basis of the area of mathematics called trigonometry, a word which traces back to the Greek words trigonan which means "triangle" and metron, meaning "to measure". In many ways, this reference triangle can be thought of as the triangle to which the word "trigonometry" owes its origin!
The above discussion focused on points on the unit circle -- points $z$ in the complex plane at distance $1$ unit from the complex number $0$ (i.e., $|z|=1$). However, we can easily extend the ideas presented there into something applicable to every $z$ in the the complex plane.
Let us start with the simple fact that for every such $z$, we have $z = 1 \cdot z$.
Recalling that multiplying any complex number (including $1$) by $z$ rotates that complex number by $arg(z)$ and scales its magnitude by $|z|$, $z$ itself must be the result of rotating $1$ by $arg(z) = \theta$ (which takes us to $\textrm{cis}(\theta)$ on the unit circle), and then scaling the result by the positive real value $r=|z|$.
Recognizing that the set of all complex values whose magnitude is $r$ forms a circle of radius $r$ centered at the origin, where we end up after the scaling -- at $r \cdot \textrm{cis}(\theta)$ -- lies on this circle, as shown below.
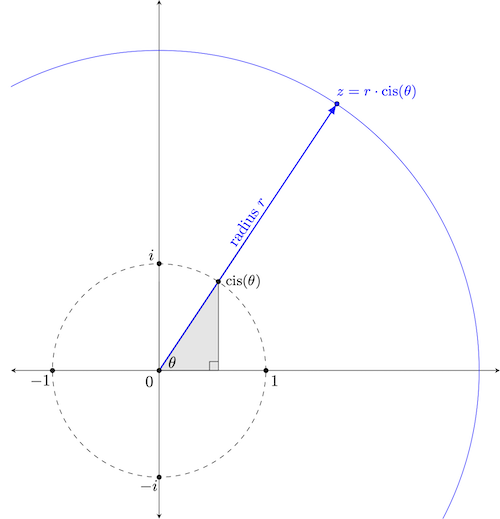
This gives us an alternate way to describe complex numbers. We already know that we can write them all in the form $a+bi$ for appropriate real values of $a$ and $b$ -- with their locations coinciding with the point $(a,b)$ in the associated Cartesian plane. Now, we can also write every complex number $z$ in the form $r \cdot \textrm{cis}(\theta)$, where $r = |z|$ and $\theta = arg(z)$. We call this the polar form of $z$, a term coined by Italian mathematician Gregorio Fontana in the 18th century.
A "polar map" of Earth
Interestingly, while $|z|$ is always positive, we can allow $r$ to be negative in polar form and everything still makes sense. We interpret a negative $r$ to be equivalent to instructions to "travel backwards" $r$ units, to continue the analogy just discussed. This is perfectly consistent with what we know already, as $$\begin{array}{rcl} -r \cdot \textrm{cis}(\theta) &=& r \cdot \textrm{cis}(\theta) \cdot (-1)\\ &=& r \cdot \textrm{cis}(\theta) \cdot \textrm{cis}(\pi)\\ &=& r \cdot \textrm{cis}(\theta+\pi) \end{array}$$ You can also get to this same result by recalling that negating a complex number (thinking in terms of transformations) is equivalent to reflecting it across the origin. This in turn can also be thought of as rotating it around the origin by $180^{\circ} = \pi$ radians.
Regardless of how you argue it, the direction of our actual movement ends up being directly opposite (backwards) from the direction we would have traveled if $r$ was positive.
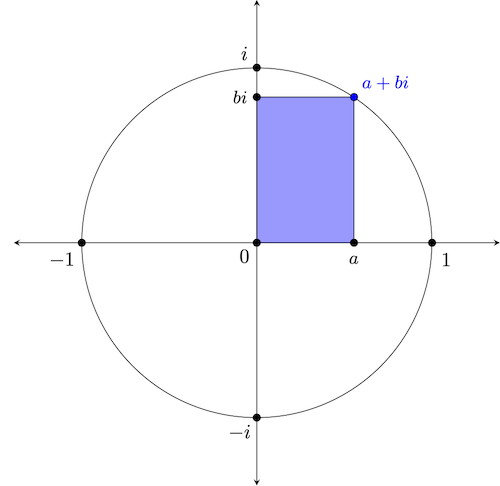
We should note before concluding this section that -- and going back to our original $a+bi$ form for a moment -- complex numbers written in this way are said to be in rectangular form. The blue rectangle in the following image perhaps provides adequate inspiration for this name:
Whenever we develop a new function, there are always questions we should ask -- things like what's the domain? ..what's the image/range? ..what interesting properties does it have? ..etc. The below addresses some of these questions for our newly-defined cosine and sine functions.
Since the inputs to both the cosine and sine functions are angles measures corresponding to rotations (which can be negative when the rotation involved is clockwise), the domain of these two functions both agree and equal the set of all real numbers, $\mathbb{R}$.
Since the related complex value $z$ for any $\theta$ lies on the unit circle, it must be the case that both the $x$ and $y$ values taken on by the cosine and sine functions respectively, must be in the interval $[-1,1]$, which then forms the image/range of these two functions. That is to say: $$-1 \le \cos \theta \le 1 \quad \textrm{ and } \quad -1 \le \sin \theta \le 1 \quad \textrm{ for all } \theta \in \mathbb{R}$$
Note that the reference triangle will always be a right triangle with base measuring $a = |\cos \theta|$ and height $b = |\sin \theta|$, with a hypotenuse always $1$ unit long (i.e., the radius of the unit circle). This, in combination with the Pythagorean theorem and the fact that $|w|^2 = w^2$ for any real value $w$, gives us the incredibly important Pythagorean Identity: $$\cos^2 \theta + \sin^2 \theta = 1 \quad \textrm{ for all } \theta \in \mathbb{R}$$
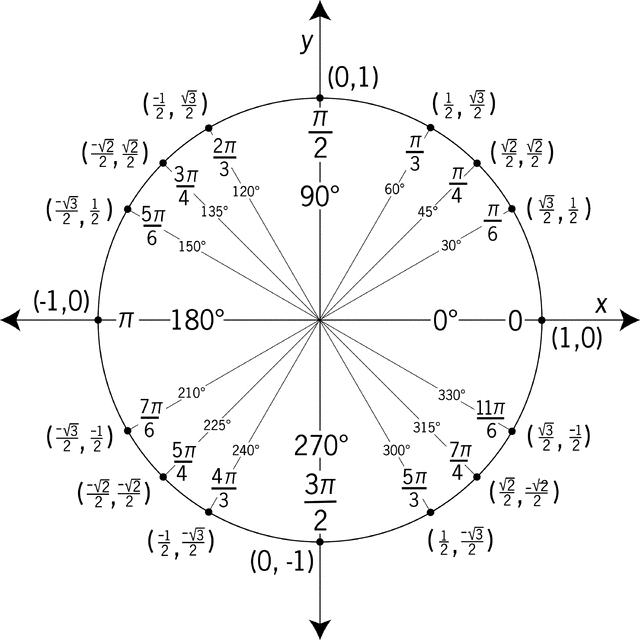
Since co-terminal angles (i.e., angles whose measures differ by either $360^{\circ} n$ or equivalently, $2\pi n$ radians, for some integer $n$) have the same coordinates, the following must be true: $$\left.\begin{array}{rcccl} \cos(\theta \pm 360^{\circ} n) &=& \cos(\theta \pm 2\pi n) &=& \cos \theta\\ \sin(\theta \pm 360^{\circ} n) &=& \sin(\theta \pm 2\pi n) &=& \sin \theta \end{array}\right\} \quad \textrm{ for all } n = 1,2,3,\ldots$$ Given that the values of the $\cos \theta$ and $\sin \theta$ don't change upon repeated addition of the same non-zero fixed amount (here, $360^{\circ}$ or $2\pi$ radians), we say these two functions are periodic (from the Greek word periodikos, meaning "coming round at intervals").
The quadrant in which some complex $z$ falls can be used to determine the signs of the corresponding values of $\cos \theta$ and $\sin \theta$, given that these are just $x$ and $y$ coordinates, respectively.
In the first quadrant, both $x$ and $y$ coordinates are positive -- and thus both $\cos \theta$ and $\sin \theta$ should be positive. In the second quadrant, $\cos \theta$ is negative, but $\sin \theta$ is positive -- again agreeing with what we expect from the $x$ and $y$ coordinates, respectively, in this quadrant, This pattern continues, as the following diagram suggests:
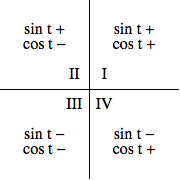
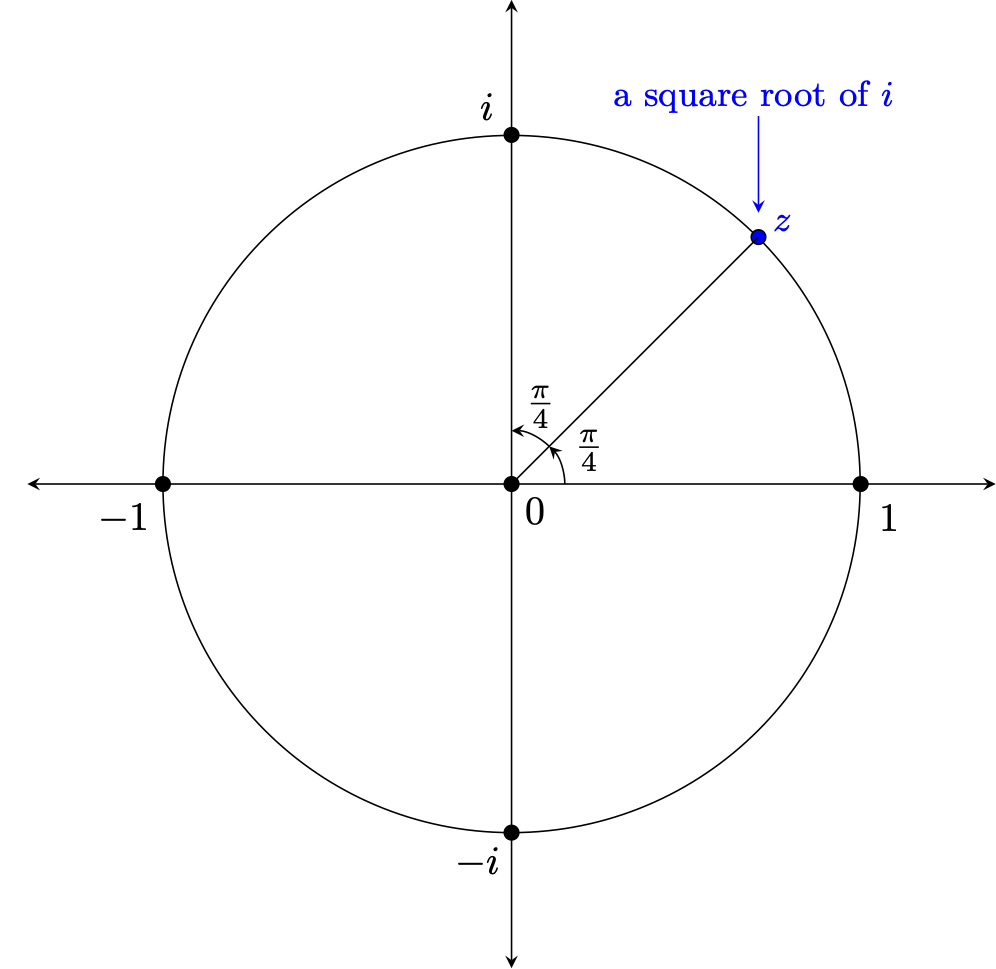
Recall that the field of complex numbers arose out of extending the real numbers with some mysterious value $i = \sqrt{-1}$. One might naturally wonder -- if dealing with the square root of a negative value required "expanding our universe of numbers" from $\mathbb{R}$ to $\mathbb{C}$, what about something like $\sqrt{i}$? Is this "universe expanding" too? ..or can we find a complex value that when squared yields $i$?
Upon a little reflection, there has to be at least one complex value that when squared yields $i$. To see this, consider how our previous exploration into products of complex numbers revealed the following two important facts that are true for any complex numbers $z_1$ and $z_2$: $$|z_1 \cdot z_2| = |z_1| \cdot |z_2| \quad \quad \textrm{ and } \quad \quad arg(z_1 \cdot z_2) = arg(z_1) + arg(z_2)$$ The first implies that the product of two complex numbers on the unit circle will also be on the unit circle. The second tells us that if we multiply a complex number by itself (i.e., square it), we will double the angle. Thus, taken together and noting that $arg(i)=90^{\circ} = \frac{\pi}{2}$ radians, it must be the case that $z = \textrm{cis}(\frac{\pi}{4}) = \textrm{cis}(45^{\circ})$ is one such square root of $i$, as suggested below.
This spawns two more questions though. We know $\textrm{cis}(\frac{\pi}{4}) = \cos(\frac{\pi}{4}) + \sin(\frac{\pi}{4})$, but what are the actual values of $\cos(\frac{\pi}{4})$ and $\sin(\frac{\pi}{4})$? Also, if $\textrm{cis}(\frac{\pi}{4})$ is one square root of $i$, are there others? (After all, for real numbers at least -- when there are any square roots of a value, there are two. One of these is positive, the other negative. However, we really can't speak of a "positive" complex value, nor a "negative" one. So what can we say?)
There are some nice ways leveraging some hopefully familiar results from geometry that we could employ to answer the first question. However, let us take a different approach so that we might answer both questions simultaneously.
Suppose there exists some complex number $z = a+bi$ (where $a,b \in \mathbb{R}$) that when squared yields $i$. That is to say, $$(a+bi)^2 = i$$ Of course, we can expand the left side and identify the real and imaginary parts of the result, and then note these same parts on the right side as well, as shown below. $$\begin{array}{rcl} a^2 + 2abi + b^2i^2 &=& i\\ a^2 + 2abi - b^2 &=& i\\ (a^2 - b^2) + (2ab)i &=& 0 + 1 \cdot i \end{array}$$ Equating the real parts between the left and right sides, and doing the same for the imaginary parts, we then have two equations that must hold: $$a^2 - b^2 = 0 \quad \quad \textrm{ and } \quad \quad 2ab = 1$$ If we solve the first for $a$ in terms of $b$ (using the "socks and shoes" strategy), we find $a = \pm b$.
Pursuing each case separately, we find...
If $a=-b$, note that substituting this into the second reveals a problem! Recall that $a \in \mathbb{R}$, which implies $a^2 > 0$. This in turn suggests the left side is negative. Of course, this is impossible when the right side equals one!
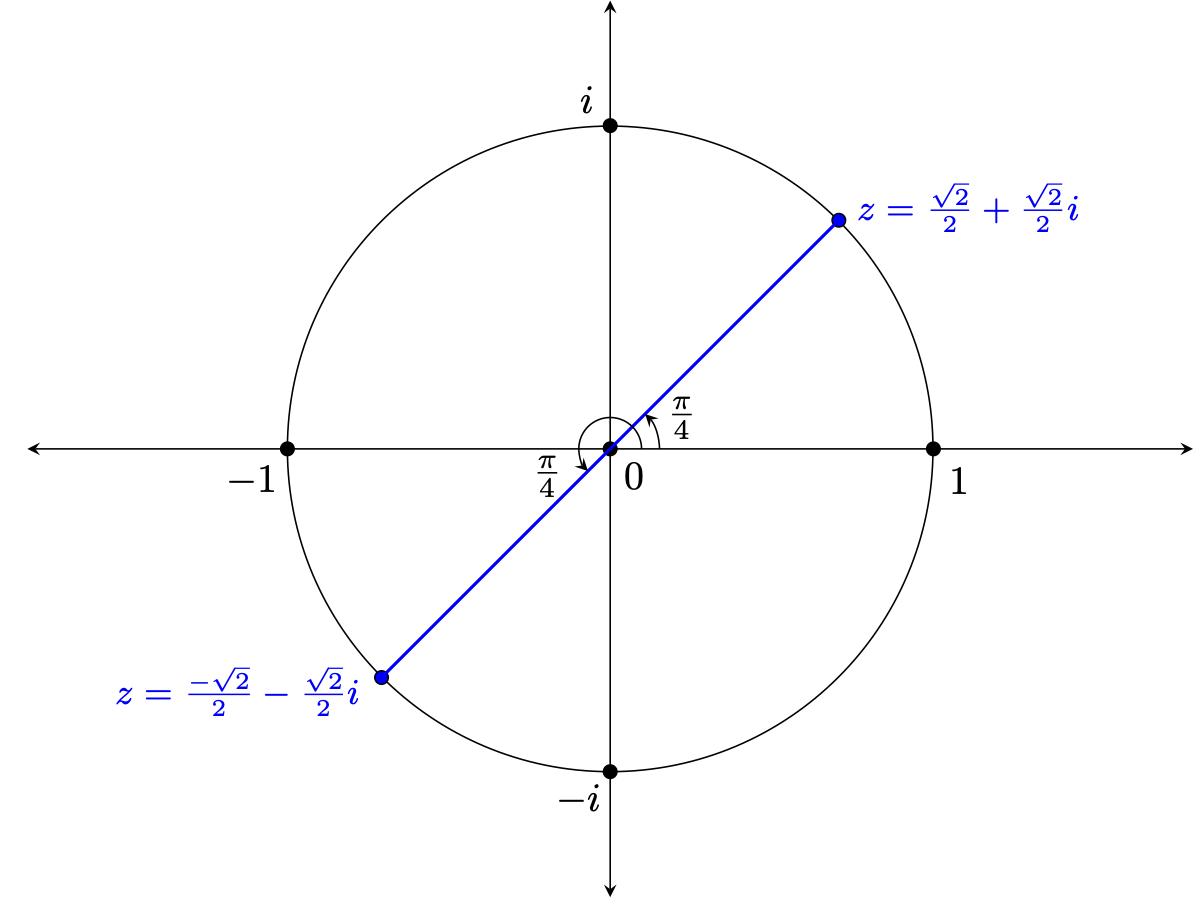
However, if $a=b$ things are more fruitful. This time, if we substitute this into the second equation and solve the resulting equation for $a$, we discover that $$\begin{array}{rcl} 2a^2 &=& 1\\ a^2 &=& \frac{1}{2}\\ a &=& \pm \frac{1}{\sqrt{2}}\\ a &=& \pm \frac{\sqrt{2}}{2} \quad \quad {\Tiny \textrm{after rationalizing the denominator}} \end{array}$$ Since $a=b$ in this case, we see there are actually two square roots of $i$, namely: $$\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}i \quad \quad \textrm{ and } \quad \quad -\frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2}i$$ Note, this can be easily verified by simply squaring each!
Interestingly, these square roots are negatives of one another, located directly across from one another on the unit circle in a manner that cuts that circle exactly in half, as shown below -- much like square roots of positive real values (except the "halves" in question are no longer the top and bottom of the unit circle).
As a bonus, we now have a couple of specific values of the cosine and sine functions. Noting our initial presumed square root of $i$ has argument $\frac{\pi}{4} \textrm{ radians } = 45^{\circ}$, and is thus in the first quadrant, we have found the values of $\cos(\frac{\pi}{4})$ and $\sin(\frac{\pi}{4})$: $$\cos(\frac{\pi}{4})=\frac{\sqrt{2}}{2} \quad \quad \textrm{ and } \quad \quad \sin(\frac{\pi}{4})=\frac{\sqrt{2}}{2}$$
We can play the same game to find a complex value that when cubed yields $i$.
First, we can feel confident that at least one such complex value must exist. Certainly, $z = \textrm{cis}(\frac{\pi}{6}) = \textrm{cis}(30^{\circ})$ satisfies the requisite criteria, given the picture below and realizing that $$|z^3| = |z|^3 = 1^3 = 1 = |i| \quad \quad \textrm{and,}$$ $$arg(z^3) = 3 arg(z) = 3 \cdot \frac{\pi}{6} = \frac{\pi}{2} = arg(i)$$
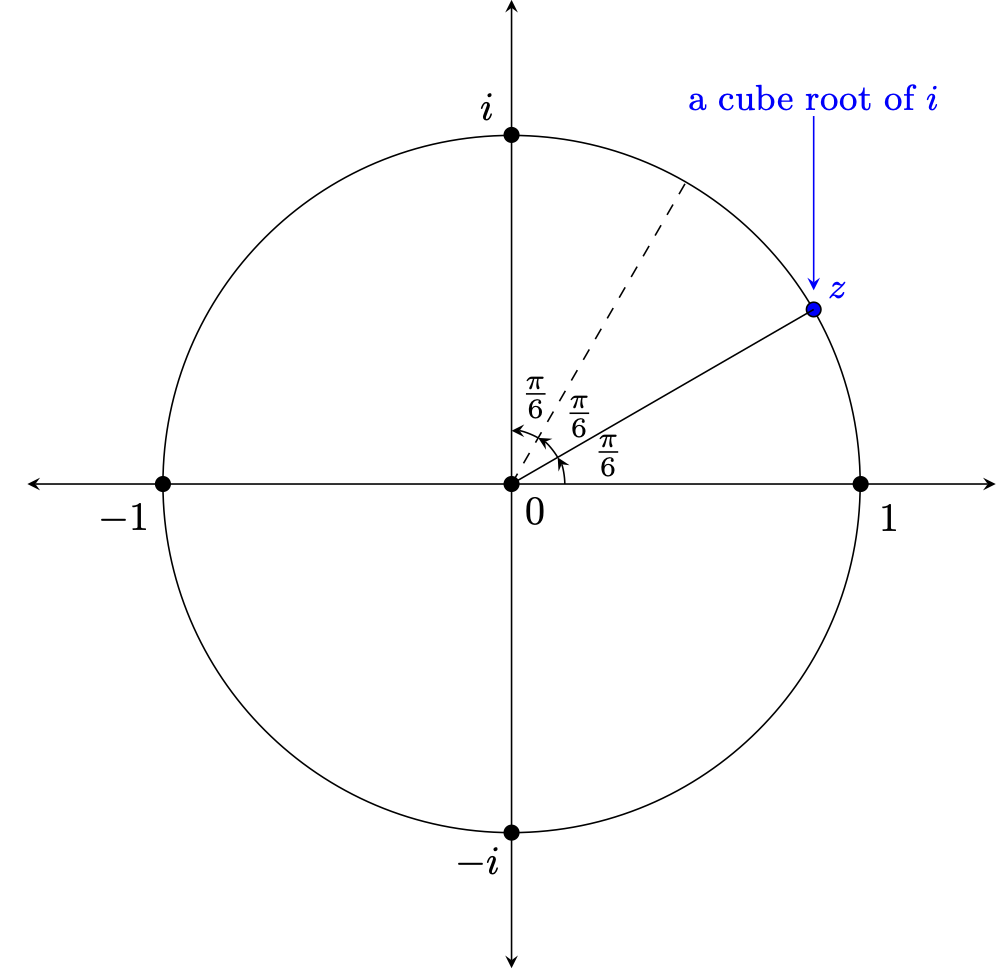
Then, as before, let us suppose $z = a + bi$ (where $a, b \in \mathbb{R}$) cubed yields $i$, and expand the power and identify its real and imaginary parts: $$\begin{array}{rcl} a^3 + 3a^2 bi + 3ab^2 i^2 + b^3 i^3 &=& i\\ a^3 + 3a^2 bi - 3ab^2 - b^3 i &=& i\\ (a^3 - 3ab^2) + (3a^2b - b^3)i &=& 0 + 1\cdot i \end{array}$$ Equating the real parts above gives us one equation relating $a$ and $b$ -- equating the imaginary parts gives us another. $$a^3 - 3ab^2 = 0 \quad \quad \textrm{ and } \quad \quad 3a^2b - b^3 = 1$$ As before, we attempt to solve the first for $a$ in terms of $b$. In this case, if we factor the left side of the first equation and apply the zero product property, we find $$a(a^2 - 3b^2) = 0 \quad \textrm{ which implies } \quad a = 0, \quad \textrm{ or } \quad a^2 -3b^2 = 0$$ The last equation can be solved via the "socks and shoes" strategy, yielding $a = \pm b\sqrt{3}$, so we end up with three possible values for $a$ that can be substituted into the equation resulting from equating the imaginary parts above, $3a^2b-b^3=1$:
If $a = 0$, we have simply $-b^3 = 1$. This can be solved via "socks and shoes" (remembering that we have required $b$ to be real) to yield $b = -1$. Thus, one cube root of $i$ is $z = 0 + (-1)i = -i$.
If $a = b\sqrt{3}$, substituting and solving for $b$ yields instead: $$\begin{array}{rcl} 3a^2b - b^3 &=& 1\\ 3(b\sqrt{3})^2 b - b^3 &=& 1\\ 9b^3 - b^3 &=& 1\\ 8b^3 = 1\\ b^3 = \frac{1}{8}\\ b = \frac{1}{2} \end{array}$$ This, in turn, means $a = \frac{\sqrt{3}}{2}$ and thus $z = \frac{\sqrt{3}}{2} + \frac{1}{2}i$ is another cube root of $i$.
If $a = -b\sqrt{3}$, substituting and solving for $b$ yields exactly the same solution as just found above (since the value of $a$ is squared, the value of $b$ does not depend on its sign). However, we do end up with a different $a$ value. In this case, we find $z = -\frac{\sqrt{3}}{2} + \frac{1}{2}i$ is yet a third cube root of $i$.
Yes, you heard correctly -- there are actually $3$ cube roots of $i$!
Further, if we mark where they occur on the unit circle, you will see they are symmetrically spaced around the circle -- quite beautifully, actually.
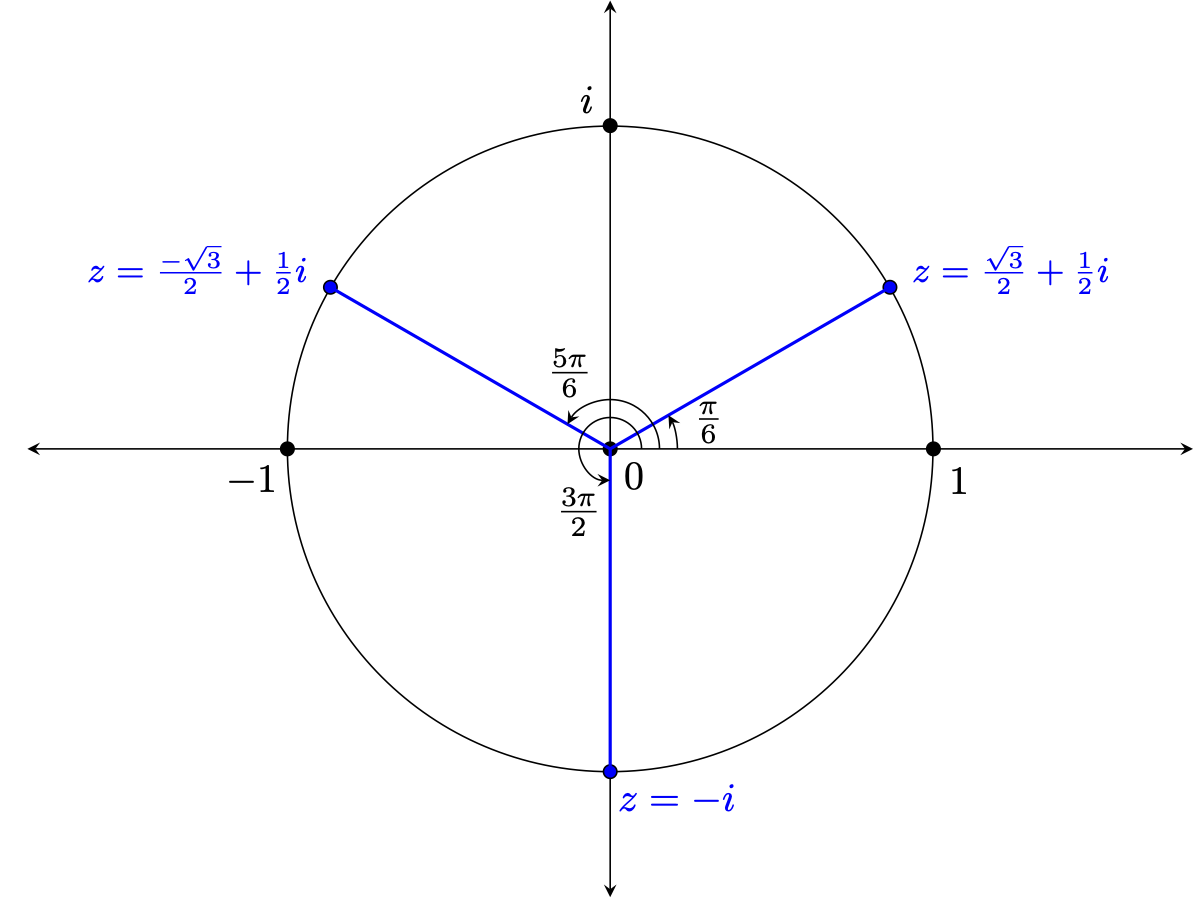
Of course, this gives us a couple more specific values of the cosine and sine functions. Noting that $\frac{\pi}{6}$ radians corresponds to the cube root in the first quadrant shown above, we have $$\cos(\frac{\pi}{6}) = \frac{\sqrt{3}}{2} \quad \quad \textrm{ and } \quad \quad \sin(\frac{\pi}{6}) = \frac{1}{2}$$
As mentioned previously, the values of $\cos \theta$ and $\sin \theta$ for the values of $\theta$ considered above can also be easily found using geometry. Using these values in conjunction with the symmetries seen in the unit circle, the values corresponding to other commonly encountered angles can also be easily found. We explore this idea below:
Note that if the related $\theta = \frac{n \pi}{2}$ where $n$ is an integer, the related point on the unit circle must be on either the $x$ or $y$ axis. Consequently, there are only four points of interest, with cosine and sine values as shown in the table and image below:
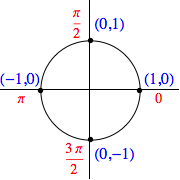
Of course, similar results are obtained for angles co-terminal to those above, as seen in the examples below: $$\cos \left( -\frac{3\pi}{2} \right) = 0, \quad \sin(5\pi) = 0, \quad \cos(-6\pi) = 1, \quad \sin \left( -\frac{5\pi}{2} \right) = -1$$
When the angles $\theta$ is $30^{\circ}$, $45^{\circ}$, or $60^{\circ}$ (or equivalently in radians: $\theta = \frac{\pi}{6}$, $\frac{\pi}{4}$, or $\frac{\pi}{3}$), we can appeal to the corresponding reference triangle and a little bit of geometry to find the exact values of $\cos \theta$ and $\sin \theta$.
Let us first consider the reference triangle for $45^{\circ} = \frac{\pi}{4}$:
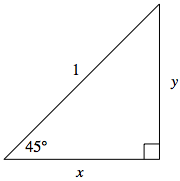 Consider a $45^{\circ}$ angle, as shown in the triangle below. Recall for a reference triangle, the hypotenuse length is always $1$ as it is a radius of the unit circle. Since the sum of angles in a triangle is $180^{\circ}$, the unmarked angle must also measure $45^{\circ}$. With two angles of the same measure, geometry tells us that the triangle is isosceles, with lengths $x$ and $y$ equal.
Consider a $45^{\circ}$ angle, as shown in the triangle below. Recall for a reference triangle, the hypotenuse length is always $1$ as it is a radius of the unit circle. Since the sum of angles in a triangle is $180^{\circ}$, the unmarked angle must also measure $45^{\circ}$. With two angles of the same measure, geometry tells us that the triangle is isosceles, with lengths $x$ and $y$ equal.
Then, the Pythagorean Theorem gives us:
$$\begin{array}{rcll} x^2 + y^2 &=& 1 & \scriptsize{\textrm{since } x = y, \textrm{we make a substitution}}\\ x^2 + x^2 &=& 1 & \scriptsize{\textrm{now we solve for } x}\\ 2x^2 &=& 1 &\\ x &=& \frac{\sqrt{2}}{2} &\scriptsize{\textrm{keeping only the positive solution, as } x \textrm{ represents a length}}\\ y &=& \frac{\sqrt{2}}{2} &\scriptsize{\textrm{again, recalling } x = y}\\ \end{array}$$Thus, we can immediately deduce: $$\cos 45^{\circ} = \frac{\sqrt{2}}{2} \quad \textrm{ and } \quad \sin 45^{\circ} = \frac{\sqrt{2}}{2}$$
We may similarly use geometry to find the values of the sine and cosine functions when applied to angles measuring $30^{\circ}$ and $60^{\circ}$.
This time we start with a $30^{\circ}-60^{\circ}-90^{\circ}$ right triangle whose hypotenuse is again one unit in length, as shown on the right.
Starting with the reference triangle for $\theta = 30^{\circ}$, we construct a congruent $30^{\circ}-60^{\circ}-90^{\circ}$ triangle directly below this one. In this way, we form a larger triangle whose angle measures are all $60^{\circ}$, as shown.
Thus, this larger triangle must then be equilateral. This means that all side lengths must be $1$ -- forcing the value of $y$ to be half that (i.e., $y = \frac{1}{2}$).
Again appealing to the Pythagorean theorem, we now have:
$$\begin{array}{rcll} x^2 + y^2 &=& 1 & \scriptsize{\textrm{then we substitute } y = \frac{1}{2}}\\ x^2 + \left(\frac{1}{2}\right)^2 &=& 1 & \scriptsize{\textrm{from here we can solve for } x}\\ 4x^2 + 1 &=& 4 &\\ x &=& \frac{\sqrt{3}}{2} & \overset{\normalsize{\textrm{again keeping only the positive value}}}{\scriptsize{\textrm{ of } x \textrm{ as it represents a length}}}\\ \end{array}$$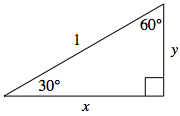
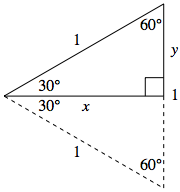
This immediately gives us
$$\cos 30^{\circ} = \frac{\sqrt{3}}{2} \quad \textrm{ and } \quad \sin 30^{\circ} = \frac{1}{2}$$For example, consider $\theta = 60^{\circ} = \frac{\pi}{3}$. Noting that the triangle whose red side points at $\frac{\pi}{3}$ must be a reflection of the other triangle across the $y=x$ line and thus congruent to it, we must have both triangles congruent to the "$30^{\circ} - 60^{\circ} - 90^{\circ}$" triangle previously discussed.
$$\textstyle{\cos \frac{\pi}{3} = \cos 60^{\circ} = \frac{1}{2} \quad \textrm{ and } \quad \sin \frac{\pi}{3} = \sin 60^{\circ} = \frac{\sqrt{3}}{2}}$$
Indeed, any angle whose reference triangle has a hypotenuse that forms either a $30^{\circ}$ angle with one of the axes will have its long side of length $\frac{\sqrt{3}}{2}$ and its short side of length $\frac{1}{2}$. Using this fact and the previously mentioned signs attached to the $x$ and $y$ coordinates in each quadrant, the cosine and sine values of any such angles will be immediate.
Similarly, for any reference triangle whose hypotenuse forms a $45^{\circ}$ angle with an axis, the sides will both have length $\frac{\sqrt{2}}{2}$. Again, combining these side lengths with what we know about the signs attached to the $x$ and $y$ coordinates in each quadrant, the cosine and sine values for these angles are also quickly determined.
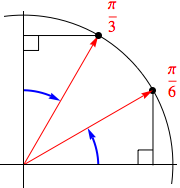
All this allows us to considerably expand our list of known sine and cosine values, as the graphic below suggests.
One might naturally wonder why the functions discussed above are named sine and cosine. The answer is fascinating! Considering the sine function first, let us begin our story in ancient India, where the Sanscrit word $jy\overline{a}$ is known to mean "bowstring". As an example, सज्य (sajya) means "furnished with a bowstring" or "strung (as a bow)".*
The connection to a bowstring is not hard to see -- consider the images below. If the circle on the right is a unit circle, note how the sine value associated with $\theta = m\angle BOC$ is the half the length of the (undrawn) "bowstring", segment $BC$. Coincidently, in the same image we can even see the "bow" as arc $\stackrel{\mbox{$\frown$}}{BAC}$, and the arrow $OA$ notched at $O$ to the (drawn) bowstring formed by the union of radii $OB$ and $OC$!

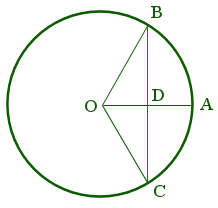
One naturally might wonder why the sine is referred to as a bowstring, when in truth it represents only half such a length. To address this, one should know that the first known table of values for the sine function can be found in the Aryabhatiya (c. 499).
Its author, Aryabhata I, actually initially uses the word ardha-jya to describe the value of the sine function -- and (appropriately) the Sanscrit word ardha means "half". However, Aryabhata eventually drops (presumably in the interests of expediency) the qualifier of ardha-, essentially abbreviating the sine value (a "half bowstring") with just the word for "bowstring".
*: See "The Practical Sanskrit-English Dictionary", 1890
Going backwards in time, the astronomers and mathematicians of India likely started using this word after reading the work of the greek Hipparchus, and seeing the greek word, χορδή (pronounced (khordḗ).
Certainly, given its pronunciation, this greek word connects to our modern "chord" of a circle -- and even the word "cord" in the sense of something like a string. More interestingly, this greek word translates directly as guts or intestines, or something made from these -- and in ancient Greece, strings of musical instruments (like the Greek Lyre shown below) and some bowstrings were made out of animal guts/sinew.**
**:As some literary evidence, for what its worth: one can find the following in the ancient greek story of the Iliad: "...he drew the bow, clutching at once the notched arrow and the string of ox's sinew" (from the Iliad 4 105-120, Murray)
Arabic astronomers then transcribe (not translate) the sanscrit word for bowstring ($jy\overline{a}$) essentially as jiba. Vowels are not always written in Arabic, and thus someone like $12^{th}$-century Gherardo of Cremona, who was translating an Arabic text on geometry into Latin, would have seen simply the Arabic equivalent to the letters "jb". As a consequence, Gherado failed to translate this word correctly, thinking it was another (i.e., جيب (jaib) -- which means "pocket".
In Latin, the word sinus means "curved or bent surface, fold, or hollow", has much in common with a "pocket".
Thus, sinus was the word to which Gherado translated to Latin the Arabic transcription of the Sanscrit version of "bowstring" (from India), which itself stemmed from the original Greek word for "chord". From there, one can easily see the final evolution into sine upon one more translation into English.
Whew! Isn't it amazing how we can trace the idea of the sine function from starting in one region of the world, and then moving to another, and another, and another still!
With regard to the origins of the word cosine, consider the following diagrams:
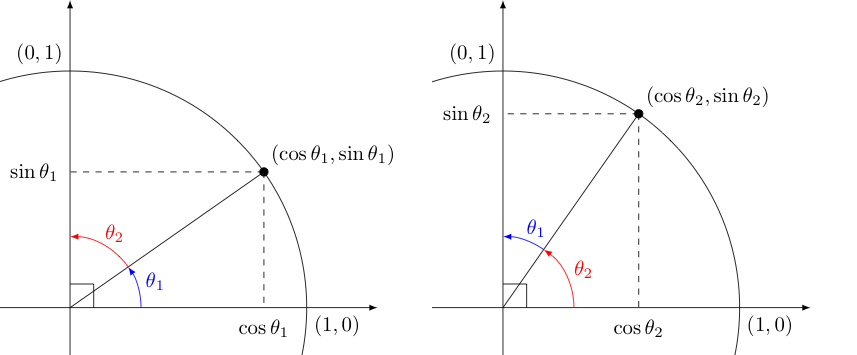
Clearly, $\theta_1$ and $\theta_2$ are complementary angles since their measures add to $90^{\circ}$ (or equivalently, their radian measures add to $\frac{\pi}{2}$).
Note that the two triangles containing angles marked in blue must be congruent as they are reflections of each other across the line $y=x$. The same can be said of the triangles containing angles marked in red. As such, we can see there is a relation between the sine and cosine of an angle $\theta_1$ and its complement $\theta_2$. Namely, $$\cos \theta_1 = \sin \theta_2 \quad \textrm{ and } \quad \sin \theta_1 = \cos \theta_2$$ Given complement to any angle $\theta$ (in radians) is $\frac{\pi}{2} - \theta$, we can equivalently say for any $\theta$ that
In this way, we see that the cosine of an angle is the sine of its complement. This important relationship is actually captured in the name of the cosine function. In Medieval Latin this function was expressed as complementi sinus (note the use of the word sinus discussed earlier). Around 1620, English mathematician Edmund Gunter abbreviated this with co.sinus -- which ultimately was contracted to the "cosine" we use today.
Recall, we defined the cosine and sine functions of an angle $\theta$ as the $x$ and $y$ coordinates of the point $(a,b)$ on the unit circle with $\arg(a+b) = \theta$. However, this is not the only route we could have taken to relate $\theta$, a point on the unit circle, and a unique pair of $x$ and $y$ values.
Rather than focusing on the coordinates of the point itself, perhaps we draw instead a tangent to the point in question and notice the $x$ and $y$ values where this tangent cuts through the two axes, as seen in the picture below at the points labeled $x$ and $y$.
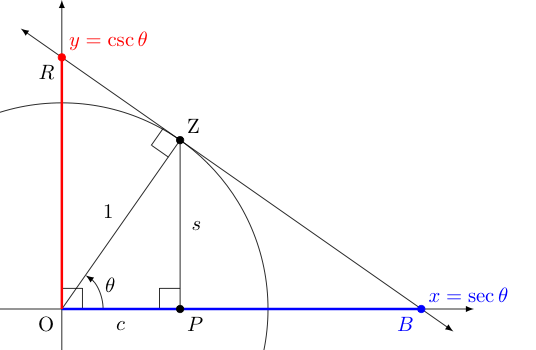
We call the function that gives the $x$ coordinate where this tangent cuts through the $x$-axis the secant function, denoted by $\sec \theta$, noting that the Latin word secare means "to cut" into pieces, not unlike the modern word "section" (when used as a verb).
In a related way, we call the function that gives the $y$-coordinate where this tangent cuts through the $y$ axis the cosecant function, denoting this by $\csc \theta$, given that the relationship between the secant of an angle and its complement is similar to that of the sine of an angle and its complement. To see this, again note that under a reflection of the entire image above over the line $y=x$, the terminal side of the angle $\theta$ (i.e., the one labeled with unit length) would move to the same for the complement of $\theta$, and the red segment would fall on the $x$-axis, as the blue segment is now.
Alternatively, we can see this relation between complements upon discovering the relationship between the secant and cosine functions. Notice that one can easily argue $\triangle BZO$ above is similar to $\triangle ZPO$, upon which we have the proportion $\sec \theta = \frac{1}{c}$.
Recognizing the convenience of picking an angle in the first quadrant, which keeps $c = \cos \theta$ and $s = \sin \theta$ (note $c$ and $s$ are distances and thus always positive, but $\cos \theta$ and $\sin \theta$ are coordinates which can sometimes be negative.), we see that in this context the secant is simply the reciprocal of the cosine function.
In the same manner, using the similarity of $\triangle OZR$ and $\triangle ZPO$, we can argue $\csc \theta = \frac{1}{s}$. Nicely, the argument above easily extends to other quadrants, making this relationship true in general:
Of course, drawing the tangent segment $\overline{RB}$ to the point $Z$ makes us wonder something. How long are the two segments $\overline{ZR}$ and $\overline{ZB}$ (shown below in orange and magenta, respectively) that comprise it?

Let us focus on $\overline{ZB}$ first. Note that $\triangle BZO$ must be similar to $\triangle ZPO$, so $ZB = \frac{s}{c}$, suggesting (at least for this quadrant) that $ZB$ is the quotient of the related sine and cosine values.
In other quadrants, we note that the quotient of the sine and cosine values can sometimes be negative (as they are both coordinates), but the segments produced there always have positive distance. Still, in these other quadrants similar arguments establish that the magnitudes of these two things always agree.
Using a similar argument involving $\triangle RZO$ and $\triangle ZPO$ establishes the length $ZR$ and the magnitude of $\cos \theta$ divided by $\sin \theta$ (i.e., the reciprocal of $ZB$).
As the lengths we are finding are both on the tangent line to the unit circle at the point corresponding to $\theta$, let us call the functions of $\theta$ that produce them the tangent and cotangent functions, denoted $\tan \theta$ and $\cot \theta$, defining these in the following way:
The typical "co-function" relationship seen for other trigonometric function pairs (i.e., sine and cosine, secant and cosecant) holds for the two functions above as well. Again, think of reflecting the entire image above over the line $y=x$ to see this.