

 |  |
Recall that we have interpreted complex multiplication in the context of rotating points in a plane representing complex numbers about the origin. Such rotations may be some part of a full rotation, a full rotation or more, or even rotations in the opposite direction (when the associated angles are negative). Exactly how much we rotate has so far been described in terms of degrees.

Hipparchus of Rhodes
Despite the existence at the time of Euclid's Elements (c. 300 BC), a text which largely set the standard for learning geometry -- that work never provided a unit of measurement for angles besides the right angle. Hipparchos thus borrowed the Babylonian division of the ecliptic -- a great circle on the celestial sphere representing the sun's apparent path during the year, so called because lunar and solar eclipses can occur only when the moon crosses it.
The ancient Babylonians had divided this circular path into 12 sections called beru (interestingly, with names that in Greek translate to Gemini, Cancer, Leo, etc.). Then, they divided each of these sections into 30 equal subsections -- allowing the position of the sun to be described in one of $12 \cdot 30 = 360$ ways. Thus, the notion of a degree -- one $360^{th}$ of a full rotation -- was born. Why $12$ sections and $30$ subdivision you ask? Likely this was due to the fact that the calendar Babylonians used at the time was based on lunar cycles (cycles of the moon). Each such cycle lasted approximately 30 days (i.e., sometimes 29, othertimes 30), with $12$ lunar cycles occurring with each year.
All that fascinating history aside, there are better things we can use to compare the sizes of angles than the number of days in a lunar cycle!
As a starting place, consider the length of the path that some complex $z$ creates as it moves from $1$ counter-clockwise around the unit circle. Recall that one complete rotation about $0$ (the origin) should result in a path $2\pi$ times as long as the radius. But how long is that, actually -- are we measuring in inches? ..in feet?
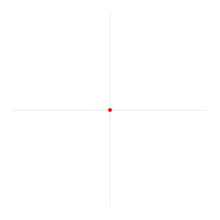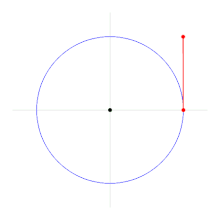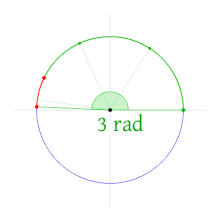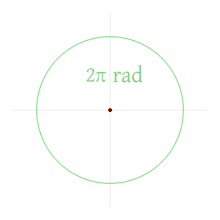 Rather than try to pick some arbitrary dimension for the measure for these lengths (which is actually not unlike the somewhat arbitrary Babylonian division of a full rotation into 360 degrees), what if we instead define the angle measure by the ratio of the length of the path $z$ takes, and the length of the radius? Note that as both would presumably be measured in the same dimension, allowing these to cancel -- leaving a "dimensionless" radian measure of the angle in question.
Rather than try to pick some arbitrary dimension for the measure for these lengths (which is actually not unlike the somewhat arbitrary Babylonian division of a full rotation into 360 degrees), what if we instead define the angle measure by the ratio of the length of the path $z$ takes, and the length of the radius? Note that as both would presumably be measured in the same dimension, allowing these to cancel -- leaving a "dimensionless" radian measure of the angle in question.
For clarity (especially when using both degrees and radians), we sometimes write angles measures expressed in radians as $\theta$ rad, but given that radians are actually dimensionless, we will more often omit the "rad" part.
Measuring angles in this way equates a full rotation of $360^{\circ}$ to a radian measure of $2\pi$, and all other angles to their proportional equivalents (for example, half of $360^{\circ}$ is $180^{\circ}$ and half of $2\pi$ is $\pi$, so $180^{\circ}$ and $\pi$ are equal angle measures. Rotations of some common radian measures are shown below:
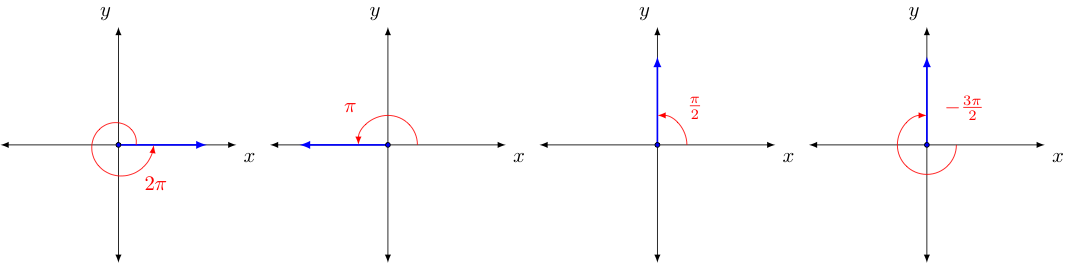
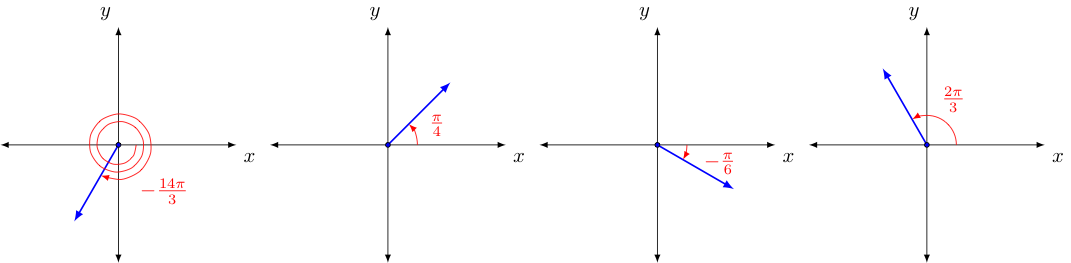
Given that a radian measure of $\pi$ is the same as $180^{\circ}$ and dividing both sides by $180$, we quickly see that $1^{\circ} = \frac{\pi}{180}$, we can then use this to easily convert the degree measure of any angle to radians and the radian measure of any angle to degrees. Some example conversions are shown below:
Convert to radians: $20^{\circ}$, $30^{\circ}$, and $-60^{\circ}$ (by multiplying by $\frac{\pi}{180^{\circ}}$):
$20^{\circ} = 20 \left( \frac{\pi}{180^{\circ}} \right) = \frac{\pi}{9}$
$30^{\circ} = 30 \left( \frac{\pi}{180^{\circ}} \right) = \frac{\pi}{6}$
$-60^{\circ} = -60 \left( \frac{\pi}{180^{\circ}} \right) = -\frac{\pi}{3}$
Convert the given radian measures to degrees: $\frac{7\pi}{6}$ rad, $-\frac{\pi}{12}$ rad, and $0.76$ rad
$\frac{7\pi}{6} = \frac{7\pi}{6} \cdot \left( \frac{180^{\circ}}{\pi} \right) = 210^{\circ}$
$-\frac{\pi}{12} = -\frac{\pi}{12} \cdot \left( \frac{180^{\circ}}{\pi} \right) = -15^{\circ}$
$0.76 = 0.76 \cdot \left( \frac{180^{\circ}}{\pi} \right) = \left( \frac{136.8}{\pi} \right)^{\circ} \approx 48.54^{\circ}$
Precisely because they do not rely on any (arbitrarily) chosen dimension, the use of radians to measure angles will greatly simplify many things in both calculus and other areas of mathematics.
We saw when we introduced complex numbers previously that multiplication of one complex number by another involves both rotation about the origin and scaling the distance from the same. Of course, if the complex numbers involved were both of unit magnitude, then only rotation was involved.
With this in mind, let us consider again the unit circle of complex values with unit magnitude. In particular, let us consider the real and imaginary parts of the $z$ on that unit circle where $\theta = arg(z)$ is known. We should recognize that knowing $\theta$ fixes exactly where this $z$ must be located in the complex plane. To see this, imagine one starts at $0$ (the origin) and then moves exactly one unit distance in a direction corresponding to $\theta$.
The real part of such a $z$ and its imaginary coefficient (and consequently the $x$ and $y$ coordinates of the corresponding point in the related coordinate plane -- also called the Cartesian plane, named after French mathematician Rene Descartes.) are also then fixed once we know $\theta$. In this way, we can think of these $x$ and $y$ coordinates as functions of $\theta$. To attach specific names to these functions, let us make the following definitions:
|
For any $\theta$, let $z = x + iy$ be the unique complex value on the unit circle (i.e., $|z| = 1$) with argument $\theta$. Then, define functions cosine and sine, denoted* $\cos \theta$ and $\sin \theta $ respectively, so that: $$\cos \theta = x = Re(z) \quad \textrm{ and } \quad \sin \theta = y = Im(z)$$ *Note that -- just like log functions -- we traditionally omit the parentheses around the input when doing so doesn't cause confusion. |
To visualize what these functions do, consider the diagram drawn on the left below. Of course, we can also (and more frequently do) draw such things instead on the related coordinate plane, as shown on the below right.
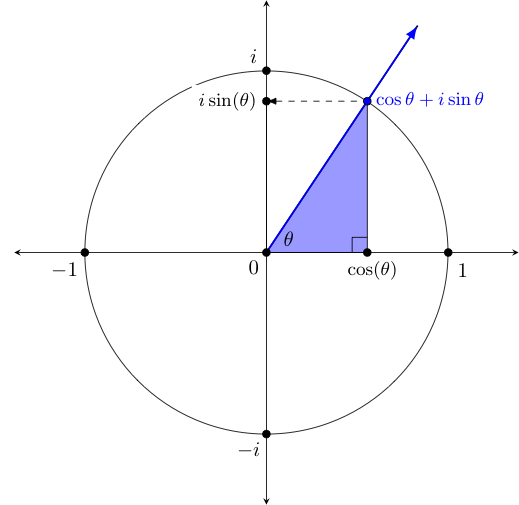
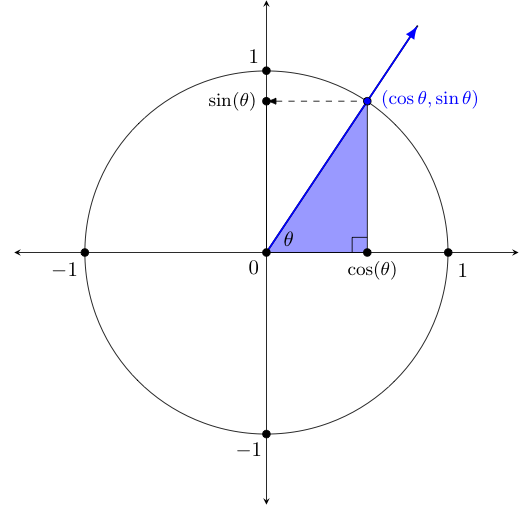
You may be curious about why we have included the shaded blue triangle in the diagram. This triangle -- formed by drawing a vertical line from the point on the unit circle to the real axis (or $x$-axis on the right) is called a reference triangle, and serves as a way to quickly compute sine and cosine values for certain commonly encountered angles. We will have more to say about it shortly.
For now, let us simply say that the cosine and sine functions form the basis of the area of mathematics called trigonometry, a word which traces back to the Greek words trigonan which means "triangle" and metron, meaning "to measure". In many ways, this reference triangle can be thought of as the triangle to which the word "trigonometry" owes its origin!
Whenever we develop a new function, there are always questions we should ask -- things like what's the domain? ..what's the image/range? ..what interesting properties does it have? ..etc. The below address some of these. Given the above equivalent ways to interpret the cosine and sine functions -- as related to the complex plane or the Cartesian plane -- let us opt for the latter in what we have to say below. That is to say, let us interpret $\cos(\theta)$ for the moment as an $x$-coordinate and $\sin \theta$ as a $y$-coordinate:
Since the inputs to both the cosine and sine functions are angles measures corresponding to rotations (which can be negative when the rotation involved is clockwise), the domain of these two functions both agree and equal the set of all real numbers, $\mathbb{R}$.
Since the related complex value $z$ for any $\theta$ lies on the unit circle, it must be the case that both the $x$ and $y$ values taken on by the cosine and sine functions respectively, must in the interval $[-1,1]$, which then forms the image/range of these two functions. That is to say: $$-1 \le \cos \theta \le 1 \quad \textrm{ and } \quad -1 \le \sin \theta \le 1 \quad \textrm{ for all } \theta \in \mathbb{R}$$
Note that the reference triangle will always be a right triangle with base measuring $a = |\cos \theta|$ and height $b = |\sin \theta|$, with a hypotenuse always $1$ unit long (i.e., the radius of the unit circle). As such, the Pythagorean theorem applies -- giving us the famed Pythagorean Identity: $$\cos^2 \theta + \sin^2 \theta = 1 \quad \textrm{ for all } \theta \in \mathbb{R}$$
Since co-terminal angles (i.e., angles whose measures differ by either $360^{\circ} n$ or equivalently $2\pi n$ radians for some integer $n$) have the same coordinates, the following must be true: $$\left.\begin{array}{rcl} \cos(\theta \pm 2\pi n) &=& \cos \theta\\ \sin(\theta \pm 2\pi n) &=& \sin \theta \end{array}\right\} \quad \textrm{ for all } \theta = 1,2,3,\ldots$$
The quadrant in which some complex $z$ falls can be used to determine the signs of the corresponding values of $\cos \theta$ and $\sin \theta$, in accordance with the following diagram:
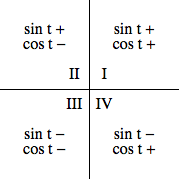
For some commonly-encountered angles of $\theta$, the values of $\cos \theta$ and $\sin \theta$ are easily found using geometry. Using these values in conjunction with the symmetries seen in the unit circle, the values corresponding to other commonly encountered angles can also be easily found. We explore this idea below:
Note that if the related $\theta = \frac{n \pi}{2}$ where $n$ is an integer, the related point on the unit circle must be on either the $x$ or $y$ axis. Consequently, there are only four points of interest, with cosine and sine values as shown in the table and image below:
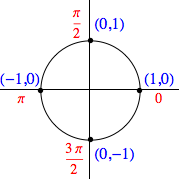
Of course, similar results are obtained for angles co-terminal to those above, as seen in the examples below: $$\cos \left( -\frac{3\pi}{2} \right) = 0, \quad \sin(5\pi) = 0, \quad \cos(-6\pi) = 1, \quad \sin \left( -\frac{5\pi}{2} \right) = -1$$
When the angles $\theta$ is $30^{\circ}$, $45^{\circ}$, or $60^{\circ}$ (or equivalently in radians: $\theta = \frac{\pi}{6}$, $\frac{\pi}{4}$, or $\frac{\pi}{3}$), we can appeal to the corresponding reference triangle and a little bit of geometry to find the exact values of $\cos \theta$ and $\sin \theta$.
Let us first consider the reference triangle for $45^{\circ} = \frac{\pi}{4}$:
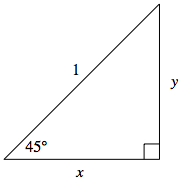 Consider a $45^{\circ}$ angle, as shown in the triangle below. Recall for a reference triangle, the hypotenuse length is always $1$ as it is a radius of the unit circle. Since the sum of angles in a triangle is $180^{\circ}$, the unmarked angle must also measure $45^{\circ}$. With two angles of the same measure, geometry tells us that the triangle is isosceles, with lengths $x$ and $y$ equal.
Consider a $45^{\circ}$ angle, as shown in the triangle below. Recall for a reference triangle, the hypotenuse length is always $1$ as it is a radius of the unit circle. Since the sum of angles in a triangle is $180^{\circ}$, the unmarked angle must also measure $45^{\circ}$. With two angles of the same measure, geometry tells us that the triangle is isosceles, with lengths $x$ and $y$ equal.
Then, the Pythagorean Theorem gives us:
$$\begin{array}{rcll} x^2 + y^2 &=& 1 & \scriptsize{\textrm{since } x = y, \textrm{we make a substitution}}\\ x^2 + x^2 &=& 1 & \scriptsize{\textrm{now we solve for } x}\\ 2x^2 &=& 1 &\\ x &=& \frac{\sqrt{2}}{2} &\scriptsize{\textrm{keeping only the positive solution, as } x \textrm{ represents a length}}\\ y &=& \frac{\sqrt{2}}{2} &\scriptsize{\textrm{again, recalling } x = y}\\ \end{array}$$Thus, we can immediately deduce: $$\cos 45^{\circ} = \frac{\sqrt{2}}{2} \quad \textrm{ and } \quad \sin 45^{\circ} = \frac{\sqrt{2}}{2}$$
We may similarly use geometry to find the values of the sine and cosine functions when applied to angles measuring $30^{\circ}$ and $60^{\circ}$.
This time we start with a $30^{\circ}-60^{\circ}-90^{\circ}$ right triangle whose hypotenuse is again one unit in length, as shown on the right.
Starting with the reference triangle for $\theta = 30^{\circ}$, we construct a congruent $30^{\circ}-60^{\circ}-90^{\circ}$ triangle directly below this one. In this way, we form a larger triangle whose angle measures are all $60^{\circ}$, as shown.
Thus, this larger triangle must then be equilateral. This means that all side lengths must be $1$ -- forcing the value of $y$ to be half that (i.e., $y = \frac{1}{2}$).
Again appealing to the Pythagorean theorem, we now have:
$$\begin{array}{rcll} x^2 + y^2 &=& 1 & \scriptsize{\textrm{then we substitute } y = \frac{1}{2}}\\ x^2 + \left(\frac{1}{2}\right)^2 &=& 1 & \scriptsize{\textrm{from here we can solve for } x}\\ 4x^2 + 1 &=& 4 &\\ x &=& \frac{\sqrt{3}}{2} & \overset{\normalsize{\textrm{again keeping only the positive value}}}{\scriptsize{\textrm{ of } x \textrm{ as it represents a length}}}\\ \end{array}$$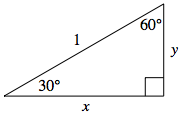
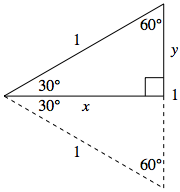
This immediately gives us
$$\cos 30^{\circ} = \frac{\sqrt{3}}{2} \quad \textrm{ and } \quad \sin 30^{\circ} = \frac{1}{2}$$For example, consider $\theta = 60^{\circ} = \frac{\pi}{3}$. Noting that the triangle whose red side points at $\frac{\pi}{3}$ must be a reflection of the other triangle across the $y=x$ line and thus congruent to it, we must have both triangles congruent to the "$30^{\circ} - 60^{\circ} - 90^{\circ}$" triangle previously discussed.
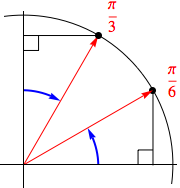
$$\textstyle{\cos \frac{\pi}{3} = \cos 60^{\circ} = \frac{1}{2} \quad \textrm{ and } \quad \sin \frac{\pi}{3} = \sin 60^{\circ} = \frac{\sqrt{3}}{2}}$$
Indeed, any angle whose reference triangle has a hypotenuse that forms either a $30^{\circ}$ angle with one of the axes will have its long side of length $\frac{\sqrt{3}}{2}$ and its short side of length $\frac{1}{2}$. Using this fact and the previously mentioned signs attached to the $x$ and $y$ coordinates in each quadrant, the cosine and sine values of any such angles will be immediate.
Similarly, for any reference triangle whose hypotenuse forms a $45^{\circ}$ angle with an axis, the sides will both have length $\frac{\sqrt{2}}{2}$. Again, combining these side lengths with what we know about the signs attached to the $x$ and $y$ coordinates in each quadrant, the cosine and sine values for these angles are also quickly determined.
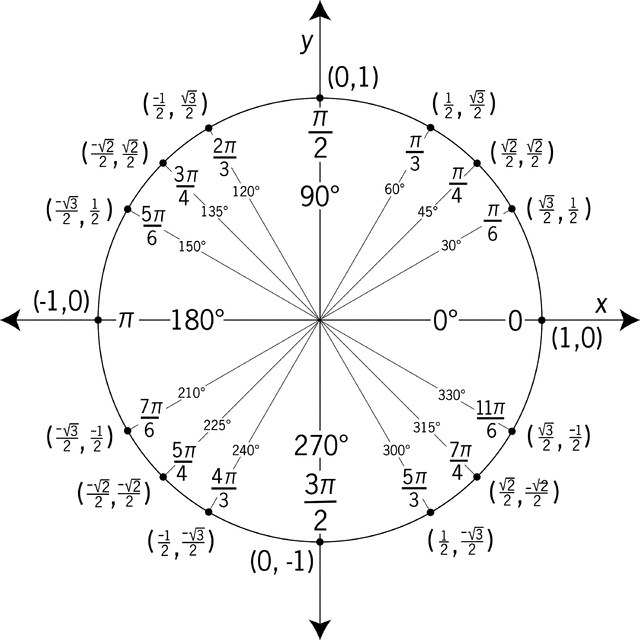
All this allows us to considerably expand our list of known sine and cosine values, as the graphic below suggests.
One might naturally wonder why the functions discussed above are named sine and cosine. The answer is interesting, in that it provides an example of how some mathematical ideas that originated in India were picked up first by the Muslims and then finally spread to Europe. The origin of sine traces back to the Sanscrit word jiya, which means "bowstring".
It is not hard to see why -- consider the images below. If the circle on the right is a unit circle, note how the sine value associated with $\theta = m\angle BOC$ is the half the length of the (undrawn) "bowstring", segment $BC$. Coincidently, in the same image we can even see the "bow" as arc $\stackrel{\mbox{$\frown$}}{BAC}$, and the arrow $OA$ notched at $O$ to the (drawn) bowstring formed by the union of radii $OB$ and $OC$!

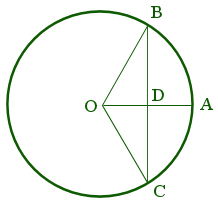
In Arabic, however the bowstring is called jiba, although vowels are not always written in Arabic, and thus someone like $12^{th}$-century Gherardo of Cremona, who was translating an Arabic text on geometry, would have seen simply the Arabic equivalent to the letters "jb". As a consequence, Gherado failed to translate this word correctly, thinking it was another (i.e., jaib) -- a word that means "curve, fold, or hollow". In Latin, the equivalent for "curve" is sinus, and from there one can more easily see the final evolution into sine upon one more translation into English.
With regard to the origins of the word cosine, consider the following diagrams:
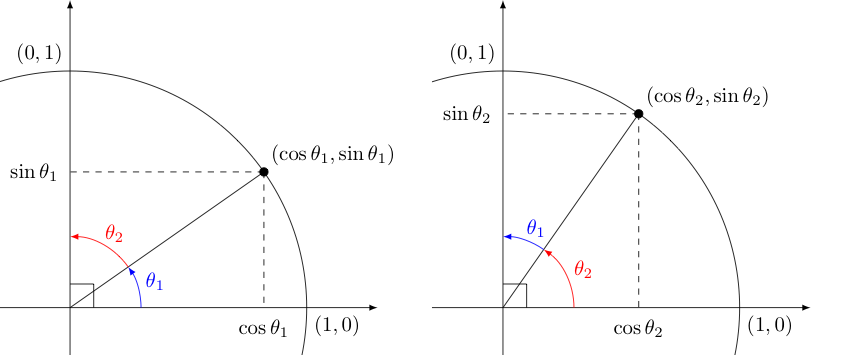
Clearly, $\theta_1$ and $\theta_2$ are complementary angles since their measures add to $90^{\circ}$ (or equivalently, their radian measures add to $\frac{\pi}{2}$).
Note that the two triangles containing angles marked in blue must be congruent as they are reflections of each other across the line $y=x$. The same can be said of the triangles containing angles marked in red. As such, we can see there is a relation between the sine and cosine of an angle $\theta_1$ and its complement $\theta_2$. Namely, $$\cos \theta_1 = \sin \theta_2 \quad \textrm{ and } \quad \sin \theta_1 = \cos \theta_2$$ Given complement to any angle $\theta$ (in radians) is $\frac{\pi}{2} - \theta$, we can equivalently say for any $\theta$ that
In this way, we see that the cosine of an angle is the sine of its complement. This important relationship is actually captured in the name of the cosine function. In Medieval Latin this function was expressed as complementi sinus (note the use of the word sinus discussed earlier). Around 1620, English mathematician Edmund Gunter abbreviated this with co.sinus -- which ultimately was contracted to the "cosine" we use today.
Recall, we defined the cosine and sine functions of an angle $\theta$ as the $x$ and $y$ coordinates of the point $(a,b)$ on the unit circle with $\arg(a+b) = \theta$. However, this is not the only route we could have taken to relate $\theta$, a point on the unit circle, and a unique pair of $x$ and $y$ values.
Rather than focusing on the coordinates of the point itself, perhaps we draw instead a tangent to the point in question and notice the $x$ and $y$ values where this tangent cuts through the two axes, as seen in the picture below at the points labeled $x$ and $y$.
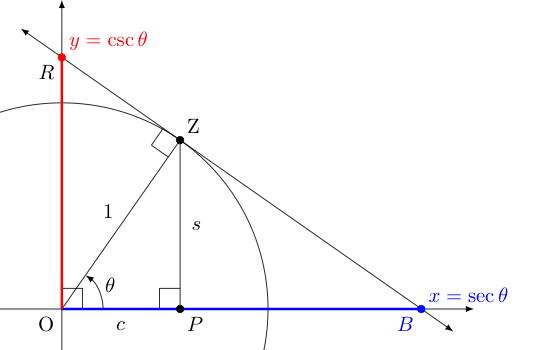
We call the function that gives the $x$ coordinate where this tangent cuts through the $x$-axis the secant function, denoted by $\sec \theta$, noting that the Latin word secare means "to cut" into pieces, not unlike the modern word "section" (when used as a verb).
In a related way, we call the function that gives the $y$-coordinate where this tangent cuts through the $y$ axis the cosecant function, denoting this by $\csc \theta$, given that the relationship between the secant of an angle and its complement is similar to that of the sine of an angle and its complement. To see this, again note that under a reflection of the entire image above over the line $y=x$, the terminal side of the angle $\theta$ (i.e., the one labeled with unit length) would move to the same for the complement of $\theta$, and the red segment would fall on the $x$-axis, as the blue segment is now.
Alternatively, we can see this relation between complements upon discovering the relationship between the secant and cosine functions. Notice that one can easily argue $\triangle BZO$ above is similar to $\triangle ZPO$, upon which we have the proportion $\sec \theta = \frac{1}{c}$.
Recognizing the convenience of picking an angle in the first quadrant, which keeps $c = \cos \theta$ and $s = \sin \theta$ (note $c$ and $s$ are distances and thus always positive, but $\cos \theta$ and $\sin \theta$ are coordinates which can sometimes be negative.), we see that in this context the secant is simply the reciprocal of the cosine function.
In the same manner, using the similarity of $\triangle OZR$ and $\triangle ZPO$, we can argue $\csc \theta = \frac{1}{s}$. Nicely, the argument above easily extends to other quadrants, making this relationship true in general:
Of course, drawing the tangent segment $\overline{RB}$ to the point $Z$ makes us wonder something. How long are the two segments $\overline{ZR}$ and $\overline{ZB}$ (shown below in orange and magenta, respectively) that comprise it?
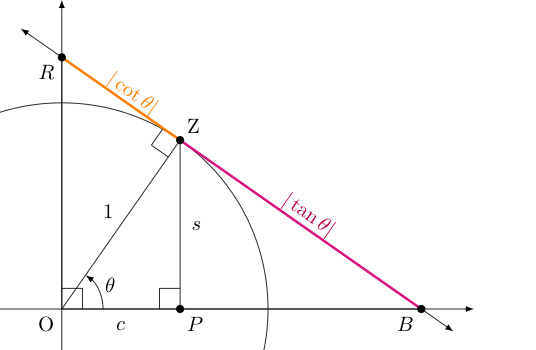
Let us focus on $\overline{ZB}$ first. Note that $\triangle BZO$ must be similar to $\triangle ZPO$, so $ZB = \frac{s}{c}$, suggesting (at least for this quadrant) that $ZB$ is the quotient of the related sine and cosine values.
In other quadrants, we note that the quotient of the sine and cosine values can sometimes be negative (as they are both coordinates), but the segments produced there always have positive distance. Still, in these other quadrants similar arguments establish that the magnitudes of these two things always agree.
Using a similar argument involving $\triangle RZO$ and $\triangle ZPO$ establishes the length $ZR$ and the magnitude of $\cos \theta$ divided by $\sin \theta$ (i.e., the reciprocal of $ZB$).
As the lengths we are finding are both on the tangent line to the unit circle at the point corresponding to $\theta$, let us call the functions of $\theta$ that produce them the tangent and cotangent functions, denoted $\tan \theta$ and $\cot \theta$, defining these in the following way:
The typical "co-function" relationship seen for other trigonometric function pairs (i.e., sine and cosine, secant and cosecant) holds for the two functions above as well. Again, think of reflecting the entire image above over the line $y=x$ to see this.
Of course, with new functions introduced, we will want to know as much as we can about them. We need to ask all the standard questions:
We aim to address all of these in this section. Let us address these in their natural pairs:
First, as we can rotate a point $(x,y)$ about the origin on the unit circle as much or as little as we desire -- and in either a positive direction (i.e., counter-clockwise) or negative direction (clockwise) -- the coordinates $x = \cos \theta$ and $y=\sin \theta$ will always be defined. Hence, the domain of both the sine and cosine functions will be the set of all reals, $\mathbb{R}$.
As for the image/range, notice that the aforementioned point $(x,y)$ is contrained to fall on the unit circle. As such, neither coordinate may get larger than $1$ in magnitude. This combined with the fact that any horizontal line drawn whose distance from the $x$-axis does not exceed $1$ intersects the unit circle at least once (much more often twice), we can see the image/range of both sine and cosine will be the interval $[-1,1]$.
Recalling that multiple rotations around the unit circle can land one in the same position multiple times throughout that rotation. As such, the $x$ and $y$ coordinates -- and thus, the outputs of the $\cos \theta$ and $\sin \theta$ functions -- will be repeated whenever the related angles are co-terminal. Seeing the same ouputs for different input angles $\theta$ means the sine and cosine functions will not be invertible.
More generally, the lack of an inverse is a property shared by every periodic function, with these defined to be a function with some non-zero $p$ called its period where $f(x) = f(x+p)$ all $x$ in its domain. Going further, noting that sine and cosine are clearly periodic, and given how the other four trigonometric functions are defined in terms of these two, all of the trigonometric functions will be periodic, and hence none will be invertible!
Still, as we have done in the past to other non-invertible functions, we can often restrict their domain to produce a related function that is invertible. For example, $f(x) = x^2$ becomes invertible if we restrict its domain to all real $x$ where $x \ge 0$. We try of course, when we restrict the domain, to ensure that every output attained by the original (non-invertible) function is also attained by the function with the restricted domain. There are often many ways to do this -- especially for periodic functions. The below shows the standard way this is accomplished for the sine function.
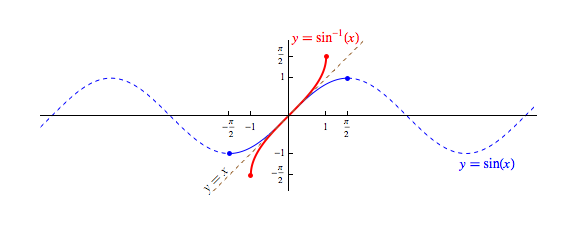
Note, the inputs above are given as radian measures, and we have switched to using an input variable of $x$ inside parentheses instead of a $\theta$ without parentheses so that we draw both graphs on the same axes. Note that (traditionally) the use of $\theta$ as a variable is highly suggestive that its associated value should be interpreted as an angle. Contrast this to the fact that the input to $sin^{-1}(x)$ is always a $y$-coordinate -- definitely not an angle! As such, we really should avoid using $\theta$ as an input variable for $sin^{-1}$. However, the use of the variable $x$ (and $y$ and $z$) traditionally only suggests their associated values are real numbers -- which both the measure of an angle in radians and the value of a sine certainly would both be!
Note that for the purpose of creating a related inverse function, we have chosen to restrict the domain to $[\frac{\pi}{2},\frac{\pi}{2}]$. This is useful on a couple of fronts. Not only do we produce an invertible function (shown in solid blue), but we also produce one that has the exact same range as the sine function with an unrestricted domain.
Additionally, while there are several intervals that do both of these things (e.g., $[\pi/2,3\pi/2]$, $[-3\pi/2,-5\pi/2]$, etc.), the interval $[-\pi/2,\pi/2]$ minimizes the magnitudes of the angles involved.
We call the inverse to the restricted-domain version of the sine function (drawn above in red) the arcsine function, denoting it by either by $\arcsin x$, or $\sin^{-1} x$. The function was likely named as was as it gives as output the measure of an "arc" (or angle) that has a given sine value.
This function behaves in many ways (but not all) as an inverse to the unrestricted domain version of $\sin x$.
For instance,
Like most inverse function pairs, the domain of $\sin^{-1} x$ is identical to the range of the $\sin x$, both being $[-1,1]$. However, the range of $\sin^{-1} x$ is only $[\pi/2,\pi/2]$, a small subset of the domain of the $\sin x$.
For any $x$ in the domain of $\sin^{-1}$, we have $\sin(\sin^{-1} x) = x$. However, $\sin^{-1} (\sin x) = x$ is true only if $x \in [-\pi/2,\pi/2]$ and false otherwise!
As always, notice the symmetry across the line $y=x$ between a function and its inverse (here, the un-named solid blue function with a restricted domain and the solid red arcsine function).
In a similar way, we can create a new invertible function that is identical to the cosine function, except with a restricted domain of $[0,\pi]$, to create a "pseudo-inverse" to the cosine function we call the arccosine function. The choice of the restricted domain here keeps the inputs as small as possible (and positive), which means the outputs of the related inverse function, called the arccosine function will also be as small as possible and positive. We denote the arccosine function by either $\arccos(x)$ or $\cos^{-1}(x)$:
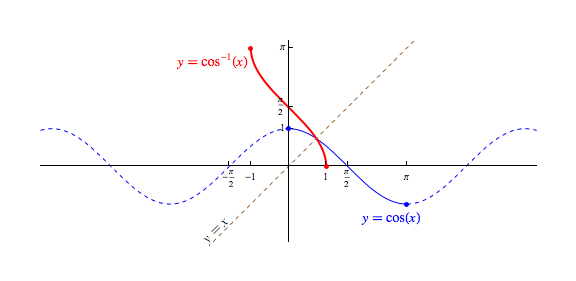
Addressing first the domain of these two functions, recall again that $$\tan \theta = \frac{\sin \theta}{\cos \theta} \quad \textrm{ and } \quad \csc \theta = \frac{\cos \theta}{\sin \theta}$$ The quotients seen above open the door to some possible domain issues, should the denominators be zero. Indeed, noting that $\cos = 0$ (i.e., one touches the $y$-axis) with every half-circle rotation from $\frac{pi}{2}$ (i.e., $90^{\circ}$), we must exclude all $\theta = \frac{\pi}{2} + n\pi$ where $n$ is an integer, from the domain of the tangent function. That is to say, the domain of the tangent is $$\{x \in \mathbb{R} \ | \ x \neq \frac{\pi}{2} + n\pi, \, \textrm{ whenever } \, n \in \mathbb{Z}\}$$ Similarly, since $\sin \theta = 0$ (i.e., one touches the $x$-axis) with every half-circle rotation from $0$, we will need to exclude all integer multiples of $\pi$ from the domain of the cotangent function. Equivalently, the domain of the cotangent function is given by $$\{x \in \mathbb{R} \ | \ x \neq n\pi, \, \textrm{ whenever } \, n \in \mathbb{Z}\}$$
Regarding the image/range for each of these functions, recall the image shared earlier showing the magnitudes of these functions as segment lengths:

By letting $\theta$ approach $\pi/2$ (i.e., $90^{\circ}$) the purple segment with length equal to the magnitude of the tangent function grows without bound. If $\theta$ instead approaches $0$ this purple length can surely be made as small as desired (including zero). Had we constructed a similar image in the second quadrant, where $\tan \theta = \frac{\sin \theta}{\cos \theta}$ is negative, we would see a similar span of magnitudes possible. Combining these, the value of $\tan(x)$ ranges over all (positive or negative) real values, $\mathbb{R}$. Finding the range of the cotangent function works similarly, and is again all reals, $\mathbb{R}$.
As we see the magnitude of $\tan(x)$ growing without bound (either in a positive or negative way) as $x$ approaches each odd multiple of $\frac{\pi}{2}$, we can expect to see some vertical asymptotes in its graph. In the image below, we can see these asymptotes drawn as vertical, dashed blue lines (they are not part of the function!)
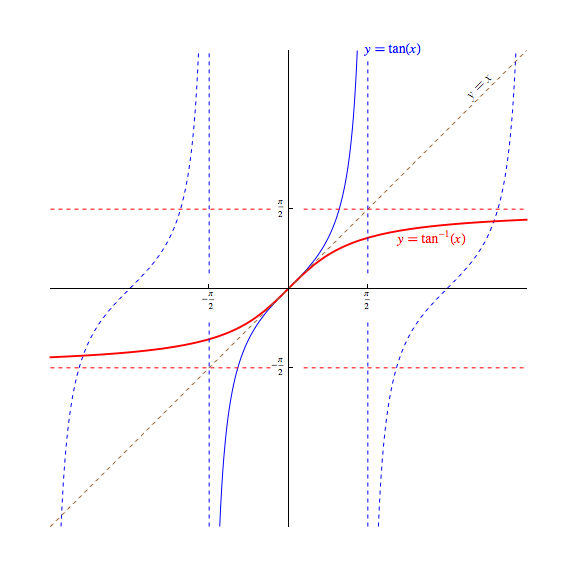
Switching discussion to the graphs and invertibility of these two functions, note that -- as mentioned before -- their periodic nature prohibits them from having inverses. However, we are free to construct for each a related domain-restricted function with an identical image/range that is invertible.
Traditionally, we restrict the domain of the tangent function to $(-\frac{\pi}{2},\frac{\pi}{2}$) so that graph can be drawn as a single continuous curve. Note in particular that the endpoints at $\pm\frac{\pi}{2}$ are not included in the restricted domain here, unlike the corresponding function used to produce $\arcsin(x)$. We call the inverse to this restricted-domain version of $\tan(x)$ the arctangent function, denoting it by $\arctan(x)$ or $\tan^{-1}(x)$.
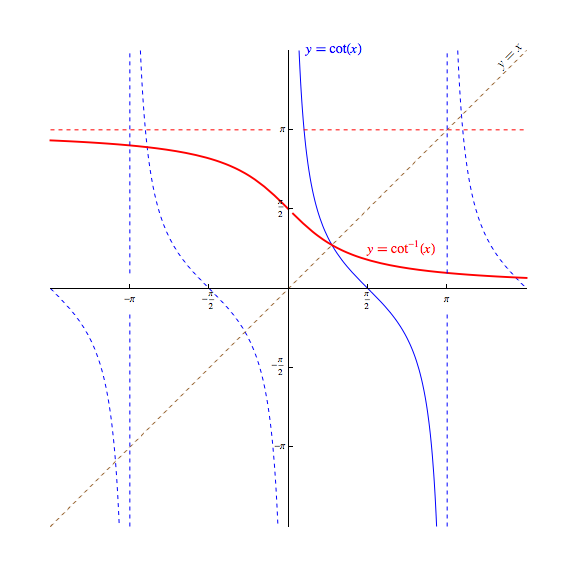
Interestingly, the choice for which "piece" of the cotangent function to invert to produce the arccotangent function is not universally agreed upon. We choose to define it to be $(0,π)$ so that the resulting arccotangent function, denoted $\textrm{arccot}(x)$ or $\cot^{-1}(x)$, is continuous and defined everywhere, and behaves in a manner more consistent with that seen in the related $\tan^{−1}(x)$ function.
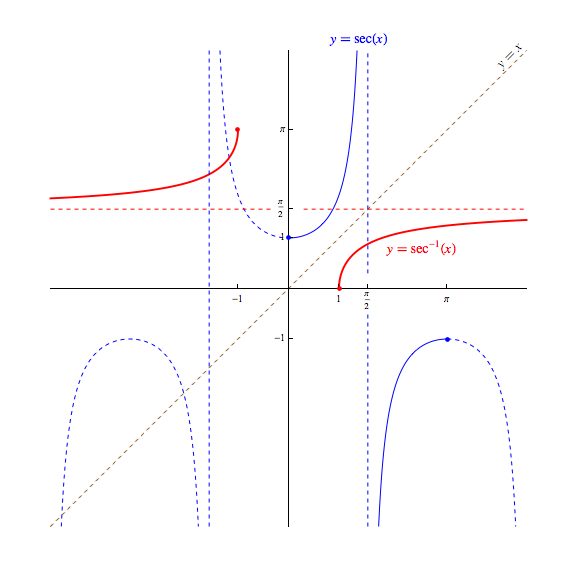
Finally, let us consider $\sec(x)$ and $\csc(x)$.
With regard to their domains, we can see in formulas describing these functions in terms of sine and cosine, we again have domain issues to worry about. $$\sec \theta = \frac{1}{\cos \theta} \quad \textrm{ and } \quad \csc \theta = \frac{1}{\sin \theta}$$ The denominators force these functions to have the same domains as the tangent and cotangent functions, respectively, with the domain of the secant function being $$\{x \in \mathbb{R} \ | \ x \neq \frac{\pi}{2} + n\pi, \, \textrm{ whenever } \, n \in \mathbb{Z}\}$$ and the domain of the cosecant function being $$\{x \in \mathbb{R} \ | \ x \neq n\pi, \textrm{ whenever } \, n \in \mathbb{Z}\}$$ Since both functions are reciprocals of a function with image/range $[-1,1]$ (all real values whose magnitude is on or less than $1$) the $\sec(x)$ and $\csc(x)$ functions must have a range of all real values whose magnitude exceed $1$! That is to say, the range of both secant and cosecant is $$\{x \in \mathbb{R} \ | \ |x| \ge 1\} = (-\infty,-1] \cup [1,\infty)$$
As another shared trait with the tangent and cotangent functions, note that being reciprocals of the cosine and sine function, as either $\cos(x)$ or $\sin(x)$ gets closer and closer to zero, the magnitude of either the $sec(x)$ or $\sin(x)$ respectively, again grows without bound. Thus, we can again expect vertical asymptotes in the graphs of the secant and cosecant funtions. Below, the blue dashed vertical lines represent these asymptotes -- these vertical lines should once again not be considered as points on the function!.
With regard to the graph of their associated "arc" functions, there is also (sadly) no universal agreement how to restrict the domain of each to create an invertible function. We choose here to define the arcsecant and arccosecant functions by choosing domain restrictions of $[0,\pi]$ and $[-\frac{\pi}{2},0) \cup (0,\frac{\pi}{2}]$, denoting the "arc" functions thus created in the typical ways:
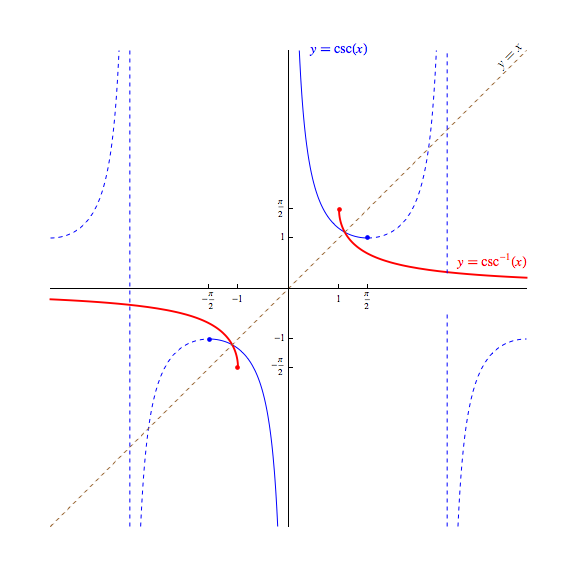
An identity is an equation whose left and right sides are equal for all values of the variables in their respective implicit domains. Some trigonometric identities (i.e., identities involving trigonometric functions) that prove useful in a great many contexts are given below, with a discussion of why each must hold. While all of these identities can be proven without appealing to complex numbers, some are proven far more easily with them!
We have already discussed the first in the list above -- which is an immediate result of how we measure the magnitude of $|z|$ for some $z = \cos(\theta) + i \sin(\theta)$ on the unit circle (i.e., when $|z| = 1$). Recall, $|z| = Re(z)^2 + Im(z)^2$
The other two pythagorean identities listed are quick consequences of this relationship. The first being the result of dividing both sides by $\cos^2 \theta$, and the second being the result of dividing both sides by $\sin^2 \theta$ instead, as the calculations below reveal:
$$\begin{array}{c|c} \displaystyle{\frac{\cos^2 \theta}{\cos^2 \theta} + \frac{\sin^2 \theta}{\cos^2 \theta} = \frac{1}{\cos^2 \theta}} \quad & \quad \displaystyle{\frac{\cos^2 \theta}{\sin^2 \theta} + \frac{\sin^2 \theta}{\sin^2 \theta} = \frac{1}{\sin^2 \theta}}\\\\ 1 + \tan^2 \theta = \sec^2 \theta & 1 + \cot^2 \theta = \csc^2 \theta \end{array}$$Examining the next picture immediately reveals the three "even/odd function identities" given above. (You do of course remember how we defined "even" and "odd" functions when we introduced functions of the form $(x) = x^n$, right?) To see how these three results can be deduced, consider the image below. Note the right triangles, sharing a common acute angle and hypotenuse length, must consequently be congruent. As such, the vertical sides of each are the same length.
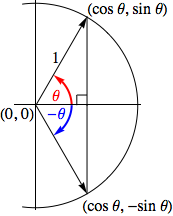
The common length of the vertical sides tell us the associated $y$-coordinates for the red and blue angles have opposite signs, but the same magnitude, which in turn implies $\sin (-\theta) = -\sin \theta$.
Meanwhile, the horizontal side common to both triangles tells us the associated $x$-coordinates for these angles are identical, and thus $\cos (-\theta) = \cos \theta$.
Knowing the values of the sine and cosine for $-\theta$, we can find the tangent for this angle as well,
$$\tan (-\theta) = \frac{\sin (-\theta)}{\cos (-\theta)} = \frac{-\sin \theta}{\cos \theta} = -\tan \theta$$Why these hold has already been discussed. They are included here only as we should now start thinking of these as tools to argue more interesting results.
These three identities are the great benefactors of the complex numbers!
Let $z_{\theta}$ denote the complex value on the unit circle with $\arg{z} = \theta$. Then, $$\begin{array}{rcl} z_{\alpha \pm \beta} &=& z_{\alpha} \cdot z_{\pm \beta}\\ &=& (\cos \alpha + i \sin \alpha )(\cos \beta + i \sin(\pm \beta))\\ &=& (\cos \alpha + i \sin \alpha )(\cos \beta \pm i \sin \beta ) \quad {\scriptstyle {\textrm{taking advantage of the even/odd property for $\sin(x)$}}}\\ &=& \left[\cos \alpha \cos\beta \mp \sin \alpha \sin \beta \right] + \left[\sin \alpha \cos \beta + \cos \alpha \sin \beta \right] \cdot i \end{array}$$ Note the last line above results from simply expanding the product immediately before, replacing $i^2$ with $-1$, and collecting the remaining multiples of $i$ together.
Now recall that $z_{\alpha \pm \beta}$ is on the unit circle, so its real part and imaginary coefficient give the cosine and sine values of its argument, $\alpha \pm \beta$, respectively. Thus, the first and second sum and difference identities are immediately established! $\require{cancel}$
All that remains is to prove the related result for the tangent. Fortunately, once the above identities are established, this one is trivial:
$$\begin{array}{rcll} \tan (\alpha \pm \beta) &=& \displaystyle{\frac{\sin \alpha \cos \beta \pm \cos \alpha \sin \beta}{\cos \alpha \cos \beta \mp \sin \alpha \sin \beta}}\\\\ &=& \frac {\displaystyle{\frac{\sin \alpha \cancel{\cos \beta}}{\cos \alpha \cancel{\cos \beta}} \pm \frac{\cancel{\cos \alpha} \sin \beta}{\cancel{\cos \alpha} \cos \beta}}} {\displaystyle{\frac{\cancel{\cos \alpha \cos \beta}}{\cancel{\cos \alpha \cos \beta}} \mp \frac{\sin \alpha \sin \beta}{\cos \alpha \cos \beta}}} & \overset{\normalsize{\textrm{after dividing by } \cos \alpha \cos \beta}}{\scriptsize{\textrm{to introduce tangents}}}\\\\ &=& \displaystyle{\frac{\tan \alpha \pm \tan \beta}{1 \mp \tan \alpha \tan \beta}} \end{array}$$Directly applying the sum formula to $\cos (\theta + \theta)$ and $\sin (\theta + \theta)$ would quickly give us formulas for $\cos 2\theta$ and $\sin 2\theta$, but we instead again appeal to complex numbers as doing so provides an efficient way to establish more general results.
To see this, consider the below -- noting how the special product rules for the squares and cubes of binomials play a significant role. As a reminder of these special product rules, recall that $(a+b)^2 = a^2 + 2ab + b^2$ and $(a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$.
Similar to how we began to prove the sum and difference formulas, let $z_{\theta}$ denote the complex value on the unit circle with $\arg{z} = \theta$. Then, $$\begin{array}{rcl} z_{2\theta} &=& z_{\theta}^2\\ &=& (\cos \theta + i \sin \theta)^2\\ &=& \cos^2 \theta + 2i\sin \theta \cos \theta + i^2 \sin^2 \theta \quad {\scriptstyle {\textrm{by the special product rule for $(a+b)^2$}}}\\ &=& (\cos^2 \theta - \sin^2 \theta) + (2\sin \theta \cos \theta) \cdot i \quad {\scriptstyle {\textrm{recalling that $i^2 = -1$ and then collecting terms}}} \end{array}$$ As argued before for the sum and difference formulas, remember that $z_{2\theta}$ is on the unit circle, so its real part and imaginary coefficient give the values of $\cos 2\theta$ and $\sin 2\theta$ seen in the box above.
To find the triple angle formula we proceed similarly, noting: $$\begin{array}{rcl} z_{3\theta} &=& z_{\theta}^3\\ &=& (\cos \theta + i \sin \theta)^3\\ &=& \cos^3 \theta + 3(\cos^2 \theta)(i\sin \theta) + 3(\cos \theta)(i^2 \sin^2 \theta) + i^3 \sin^3 \theta \, \, {\scriptstyle {\textrm{by the special product rule for $(a+b)^3$}}}\\ &=& (\cos^3 \theta - 3\cos \theta \sin^2 \theta) + (3\cos^2 \theta \sin \theta - \sin^3 \theta) \cdot i \quad {\scriptstyle {\textrm{recalling that $i^2 = -1$, and therefore $i^3 = -i$}}} \end{array}$$ Again recalling $z_{3\theta}$ is on the unit circle, its real part and imaginary coefficient must give the values for $\cos 3\theta$ and $\sin 3\theta$ also seen in the box above.
The Pythagorean identity $\cos^2 \theta + \sin^2 \theta = 1$ provides an easy way to find an alternate form for any expression involving either $\cos^2 \theta$ or $\sin^2 \theta$, as we may solve it for these two expressions to find $$\cos^2 \theta = 1 - \sin^2 \theta \quad \textrm{ and } \quad \sin^2 \theta = 1 - \cos^2 \theta$$ Note that when we apply these to the double-angle identity for cosine, we can produce replacements for $\cos 2\theta$ that involve only a single trigonometric function. To see this, consider the following. $$\begin{array}{rcl} \cos 2\theta &=& \cos^2 \theta - \sin^2 \theta\\ &=& \cos^2 \theta - (1 - \cos^2 \theta)\\ &=& 2\cos^2 \theta - 1 \end{array}$$
and
$$\begin{array}{rcl} \cos 2\theta &=& \cos^2 \theta - \sin^2 \theta\\ &=& (1 - \sin^2 \theta) - \sin^2 \theta\\ &=& 1 - 2 \sin^2 \theta \end{array}$$We may do something similar with the triple angle formulas, as seen below: $$\begin{array}{rcl} \cos 3\theta &=& \cos^3 - 3\cos \theta \sin^2 \theta\\ &=& \cos^3 \theta - 3\cos \theta (1-\cos^2 \theta)\\ &=& \cos^3 \theta - 3\cos \theta + 3\cos^3 \theta\\ &=& 4\cos^3 \theta - 3\cos \theta \end{array}$$ and $$\begin{array}{rcl} \sin 3\theta &=& 3\cos^2 \theta \sin \theta - \sin^3 \theta\\ &=& 3(1-\sin^2 \theta) \sin \theta - \sin^3 \theta\\ &=& 3\sin \theta - 3\sin^3 \theta - \sin^3 \theta\\ &=& 3\sin \theta - 4\sin^3 \theta \end{array}$$
Lastly, if we take these two alternate forms for $\cos 2\theta$ and solve for $\sin^2 \theta$ and $\cos^2 \theta$, respectively -- we produce the half angle identities,
Knowing the half angle identities in the above form will be the most useful for applications in calculus. That said, why these identities are called the "half angle" identities is made more clear upon making a substitution of $x = 2\theta$ and then taking a square root:
$$\begin{array}{c} \left| \cos \left( \frac{x}{2} \right) \right| &=& \displaystyle{\sqrt{\frac{1+\cos x}{2}}}\\\\ \left| \sin \left( \frac{x}{2} \right) \right| &=& \displaystyle{\sqrt{\frac{1-\cos x}{2}}} \end{array}$$In this way, we can discover the magnitudes of the sine and cosine for half an angle if we know the cosine of the full angle. As for whether the sine and cosine are positive or negative, this is most easily managed by determining in which quadrant the half angle lies.
To prove that a trigonometric equation is an identity, one typically starts by trying to show that either one side of the proposed equality can be transformed into the other, or that both sides can be transformed into the same expression.
In other words, suppose $A$ and $B$ are some trigonometric expressions and we are trying to determine if $A=B$.
We hope that both expressions will simplify to some common form $C$, as if we can show the following:
$$\begin{array}{rclcrcl} A &=& A_1 \quad && \quad B &=& B_1\\ &=& A_2 && &=& B_2\\ &=& \cdots & \textrm{and} & &=& B_3\\ &=& A_n && &=& B_4\\ &=& C && &=& \cdots\\ & & && &=& B_m\\ & & && &=& C \end{array}$$then we will know
$$A = A_1 = A_2 = \cdots = A_n = C = B_m = \cdots = B_2 = B_1 = B$$and thus,
$$A = B$$That is our general "plan of attack" -- although, we might get lucky and the sequence of $A_1, A_2, \cdots$ will terminate in $B$, or the sequence $B_1, B_2, \cdots$ will terminate in $A$, which then shortens our argument a bit.
There are some basic strategies to help us get to that common form $C$ as efficiently as possible:
Only manipulate one side of the proposed identity at a time. Start by attempting to simplify the more complicated side first, as which steps one should take will likely be more obvious for this side.
First "trigonometrically simplify" the side in question.
One should try rewriting all of trigonometric functions involved in terms of sines and cosines, unless there is a compelling reason not to do this.
Example
$$\begin{array}{rcl} \tan \theta + 2\csc \theta &=& \displaystyle{\left( \frac{\sin \theta}{\cos \theta} \right) + 2\left( \frac{1}{\sin \theta} \right)}\\ &=& \cdots \end{array}$$Likewise, if you see trigonometric functions involving more than one angle measure, try to use known identities to rewrite things so that only a single angle measure is involved.
Example
$$\begin{array}{rcl} \displaystyle{\frac{\cos 2\theta + \sin \theta}{\sin 2\theta + \sin(-\theta)}} &=& \displaystyle{\frac{ (\cos^2 \theta - \sin^2 \theta) + \sin \theta}{2\sin \theta \cos \theta - \sin \theta}}\\ &=& \cdots \end{array}$$If one side can be written in terms involving (perhaps multiple occurrences of) a single trigonometric function of a single angle measure, doing so may help. In particular, this often helps in cases where one side of the proposed identity is already in this form, and the other side consists of a mixture of trigonometric functions.
Example
$$\begin{array}{rcll} \displaystyle{\frac{\cos 2\theta}{\cos(\pi/2-\theta)}} &=& \displaystyle{\frac{1 - 2\sin^2 \theta}{\sin \theta}} & \overset{\normalsize{\textrm{assuming we were trying to get}}}{\scriptsize{\textrm{things in terms of only sine functions}}}\\ &=& \cdots \end{array}$$As the previous examples attest, trigonometrically simplifying an expression sometimes makes it algebraically more cumbersome. This can actually be a good thing -- as it gives us a direction to proceed. Specifically -- after trigonometrically simplifying a side of the proposed identity -- one can next focus on "algebraically simplifying" it.
Complex fractions (i.e., fractions with fractions in either the numerator or denominator) should be collapsed
Example
$$\begin{array}{rcll} \frac{\displaystyle{\frac{\sin \theta}{\cos^2 \theta}}}{\displaystyle{1 + \frac{1}{\cos \theta}}} &=& \displaystyle{\frac{\sin \theta}{\cos^2 \theta + \cos \theta}} & \scriptsize{\textrm{ after multiplying by } \displaystyle{\frac{\cos^2 \theta}{\cos^2 \theta}}}\\ &=& \cdots \end{array}$$When fractional expressions appear in a sum or difference, these terms should be combined into a single fraction, finding common denominators as necessary. The resulting fractional expression may, upon factoring, admit a common factor that can be cancelled -- or may be simplified in some other fashion.
Example$\require{cancel}$
$$\begin{array}{rcll} \displaystyle{\frac{1}{\sin^2 \theta} + \frac{1}{\cos^2 \theta} + \frac{\sin \theta \cos^2 \theta - 1}{\sin^2 \theta \cos^2 \theta}} &=& \displaystyle{\frac{\cos^2 \theta + \sin^2 \theta - 1 + \sin \theta \cos^2 \theta}{\sin^2 \theta \cos^2 \theta}}\\\\ &=& \displaystyle{\frac{1 -1 + \sin \theta \cos^2 \theta}{\sin^2 \theta \cos^2 \theta}}\\\\ &=& \displaystyle{\frac{\sin \theta \cos^2 \theta}{\sin^2 \theta \cos^2 \theta}}\\\\ &=& \displaystyle{\frac{1}{\sin \theta}}\\\\ &=& \cdots \end{array}$$Try to manipulate the side in question into the same "form" as the other side. For example, suppose one is attempting to simplify the left side of a proposed identity and the right side is a product. Then one should attempt to factor the left side, so that it is also expressed as a product.
Also, when the left and right sides get to the point where there is a partial "match", one should leave the matched parts alone from that point forward, and only manipulate the parts that still don't look like one another.
Example
Show $\sin \theta \cos^2 \theta - \sin \theta = -\sin^3 \theta$ is an identity.
Starting with the left side, we have...
$$\begin{array}{rcll} \sin \theta \cos^2 \theta - \sin \theta &=& \sin \theta (\cos^2 \theta - 1) & \overset{\normalsize{\textrm{notice the right side, } -\sin^3 \theta, \textrm{ is a product, so}}}{\scriptsize{\textrm{we factor the left side to have the same form}}}\\\\ &=& \cdots\\\\ &=& \sin \theta (-\sin^2 \theta) & \overset{\normalsize{\textrm{working backwards from the sought expression below}}}{\scriptsize{\textrm{we expose a "match" of } \sin \theta \textrm{ with the above}}}\\\\ &=& -\sin^3 \theta\\\\ \end{array}$$To fill in the missing steps above, we just need to "massage" $(\cos^2 \theta - 1)$ into $(-\sin^2 \theta)$. This of course is immediate, given the Pythagorean identity $\cos^2 \theta + \sin^2 \theta = 1$.
It may be the case that in the course of trying to prove a given equation is an identity, one begins to suspect that it is not.
In such situations, one should test whether the equation's left and right sides are actually equal by plugging in some values for the variables it contains. Remember, one only needs a single counter-example to prove an equation is not an identity.
If however, one tests a particular value (or set of values) and the left and right sides of the given equation agree in value, that particular test is inconclusive -- and a decision must be made whether to continue the search for a counter-example and test additional values, or to return to trying to prove the given equation is an identity.
To have the best chance of selecting values that will show a given equation is not an identity, one should keep the following in mind:
While picking angle measures that are integer multiples of $\pi/2$ will lend itself to easy evaluation of the expressions involved in the equation, such values will often fail to reveal an equation is not an identity due to the fact that either the sine or cosine for these angle measures will be zero.
Example
The following is clearly not an identity: $\sin \theta = \cos \theta + \sin \theta$. However, if one tests this with either $\theta = \pi/2$ or $\theta = 3\pi/2$, the results will be inconclusive, as the left and right sides will have the same value (i.e., $1$ in the first case, $-1$ in the second).
A similar problem presents itself when testing a proposed identity with angle measures that are odd integer multiples of $\pi/4$, but for a different reason. For these angle measures, recall the sine and cosine values are either identical or differ only in sign. This too can create inconclusive results for an equation that is not actually an identity.
Example
The following is clearly not an identity: $2\sin \theta= \cos \theta + \sin \theta$. However, if one tests this with either $\theta = \pi/4$ or $\theta = 5\pi/4$, the results will be inconclusive, as both sides evaluate to $\sqrt{2}$.
Testing a proposed identity with angle measures that are integer multiples of $\pi/6$ or $\pi/3$ (when reduced) can be good first choices, as the exact values of the trigonometric functions are easy to find, and the problems seen above don't occur.