

 |  |
In the last section, we solved for where some simple linear expressions were equal to zero (e.g., $2x+3=0$). While doing so was likely easy and familar for most readers -- even in solving these simple equations there is a kernal of a much more powerful equation-solving strategy, one that can help solve not only polynomial equations but many others!

Now, consider the following equation -- which notably has only a single occurrence of $x$, the variable whose value we wish to find. $$(4x - 6)^3 = 8$$ In particular, note how the value on the left side is computed for any given value of $x$. By the order of operations: we first multiply $x$ by 4, then we subtract $6$ from that value, then we cube the result.
If we envision each of these actions as functions $f(x) = 4x$, $g(x) = x-6$, and $h(x) = x^3$, then we can think of the left side as a composition of these three functions: $$h(g(f(x))) = 7$$ Just as we first covered each foot with a sock, and then covered that with a shoe, and then put shoe covers over that -- here, we first applied $f$ to $x$, and then applied $g$ to that, and then applied $h$ to that last result.
If we wish to undo the effect of applying these functions on $x$, and reveal $x$'s value -- in the same way we reveal our bare feet, we'll need to undo each action, but in reverse order. To "undo" the effect of each function, we simply apply its inverse (presuming it exists) to both sides. Doing this for each function involved produces the solution for $x$ we seek: $$\begin{array}{rcl} h(g(f(x))) &=& 7\\ g(f(x)) &=& h^{-1}(7)\\ f(x) &=& g^{-1}(h^{-1}(7))\\ x &=& f^{-1}(g^{-1}(h^{-1}(7))) \end{array}$$ In solving equations using this strategy, in practice we generally don't actually name the individual (tiny) functions involved as we did above -- we simply apply the appropriate inverses, in the appropriate order, as seen below: $$\begin{array}{rcll} (4x-6)^3 &=& 7 & {\Tiny \textrm{The last function applied on the left was cubing, so we undo this by taking a cube root of both sides}}\\ 4x-6 &=& \sqrt[3]{7} & {\Tiny \textrm{The last function applied on the left subtracted $6$, so we undo this by adding $6$ to both sides}}\\ 4x &=& \sqrt[3]{7} + 6 & {\Tiny \textrm{The last function applied on the left multiplied by $4$, so we undo this by dividing by $4$ on both sides}}\\ x &=& (\sqrt[3]{7} + 6)/4 \end{array}$$ As one might imagine, this strategy allows us to solve a great many equations -- provided there is only one occurrence of the variable, and all the functions involved are invertible.
With this in mind, let us remind ourselves of some common pairs of inverse functions (assume $c$ represents some constant value in the table below): $$\begin{array}{|c|c|l|}\hline x + c & x - c & \\\hline cx & x/c & \textrm{presuming $c \neq 0$}\\\hline 1/x & 1/x & \\\hline x^c & \sqrt[c]{x} & \textrm{presuming $c$ is an odd integer}\\\hline c^x & \log_c x & \textrm{presuming $c \gt 0$ and $c \neq 1$}\\\hline \end{array}$$
Importantly, we can undo either function of each pair with the other, as the following example illustrates:
|
Question Solution $$\begin{array}{rcl} \log_2 \left(\cfrac{\sqrt[5]{7^x + 1}}{4}\right) &=& 3\\ \cfrac{\sqrt[5]{7^x + 1}}{4} &=& 2^3\\ \sqrt[5]{7^x + 1} &=& 4\cdot 2^3\\ 7^x + 1 &=& (4 \cdot 2^3)^5\\ 7^x &=& (4 \cdot 2^3)^5 - 1\\ x &=& \log_7 ((4 \cdot 2^3)^5 - 1) \end{array}$$ Of course, we should simplify the expression found on the right side as much as possible when we are done, so that our answer looks as "pretty" as it can. Depending on the context, it might even help to approximate the overall value found (with a calculator): $$x = \log_7 33554431 \approx 8.90518$$ |
For equations where the variable whose value we seek occurs in more than one place, we can't immediately apply this strategy. Of course, if we could write an equivalent equation with only one occurrence of the variable, then we can apply it to this new equation.
Sometimes we are lucky enough that simply "collecting like terms" and/or adding or subtracting a common term from both sides will do the trick:
|
Question Solution $$\begin{array}{rcll} 7m^3 + 2m + 3m + 5 &=& 4m^3 + 5m - 8 & {\Tiny \textrm{collecting like terms $2m$ and $3m$ reduces the number of terms with $m$ by one}}\\ 7m^3 + 5m + 5 &=& 4m^3 + 5m - 8 & {\Tiny \textrm{subtracting $4m^3$ from both sides again reduces the number of terms with $m$}}\\ 3m^3 + 5m + 5 &=& 5m - 8 & {\Tiny \textrm{subtracting $5m$ from both sides gets rid of TWO terms involving $m$}}\\ 3m^3 + 5 &=& -8 & {\Tiny \textrm{we can use "socks and shoes" on what's left, since there is only one $m$ remaining}}\\ 3m^3 &=& -13 & \\ m^3 &=& \frac{-13}{3} & \\ m &=& \sqrt[3]{\frac{-13}{3}} \approx -1.6303& \end{array}$$ |
Other times, we need to be more creative. For example, notice below how factoring the left side into a perfect cube helps rewrite the equation so that we only have one occurrence of $x$. This allows us to use the "socks and shoes" to solve the equation from there.
|
Question Solution $$\begin{array}{rcll} x^3 + 6x^2 + 12x + 8 &=& 5\\ (x+2)^3 &=& 5\\ x+2 &=& \sqrt[3]{5}\\ x &=& \sqrt[3]{5} - 2 \approx -0.290024 \end{array}$$ |
Here's another example, where we use both factoring and properties of logarithms to collapse multiple occurrences of $x$ into a single occurrence, allowing us to proceed from there with "socks and shoes":
|
Question Solution $\require{cancel}$ $$\begin{array}{rcl} \displaystyle{\log_{10} (x^2+1) + \log_{10} (x^4 + 2x^2 + 1)} &=& 3 \quad {\Tiny \textrm{ first we recognize the square of a binomial}}\\ \displaystyle{\log_{10} (x^2+1) + \log_{10} (x^2 + 1)^2} &=& 3 \quad {\Tiny \textrm{ a property of logs will help us reduce the number of $x$ variables we have}}\\ \displaystyle{\log_{10} (x^2+1)^3} &=& 3 \quad {\Tiny \textrm{ with one occurrence of $x$ left, we can use "socks and shoes" from here}}\\ \displaystyle{\cancel{10}^{\cancel{\log_{10}} (x^2 + 1)^3}} &=& \displaystyle{10^3} \quad {\Tiny \textrm{notably first using the inverse of $\log_{10} x$ (i.e., $10^x$) to eliminate the log}}\\ \displaystyle{(x^2+1)^3} &=& 10^3\\ x^2+1 &=& 10\\ x^2 &=& 9\\ x &=& \pm 3 \end{array}$$ |
Of course, we must always be aware that some equations just don't have solutions to be found. Fortunately, following our natural instincts and trying to solve the equation as if there was a solution to be found often naturally leads us to solving a simpler equation where the lack of solution is easy to see. Consider the following example:
|
Question Solution Similar to what we did from the third step forward in the previous problem's solution, we first might subtract $3x$ from both sides to reduce the number of occurances of $x$ in our equation. In this case, however, we then see a square of a binomial on the left side: $$\begin{array}{rcll} x^2 + 5x + 1 &=& 3x - 3\\ x^2 + 2x + 1 &=& -3\\ (x+1)^2 &=& -3 \end{array}$$ As soon as we see this, we can stop looking for a solution -- as no real value squared yields $-3$. |
There are other times when we are forced to conclude no solution exists to certain equations. For example, suppose one deduced upon solving for some $x$ that $x+1=x$, or that $\frac{1}{x} = 0$. There are countless other examples. The point is to be alert as to when continued work will be futile, and to not waste further time on an equation when realizing this is the case!
In the next example, notice how we combine factoring, the zero product property (which we used previously to find roots of polynomial equations), and "socks and shoes" to solve the equation:
|
Question Solution First, we avoid the temptation to factor out an $x$ given that the right side is non-zero. Let us subtract the $16$ from both sides first to manufacture a $0$ on the right, so that we might use the zero-product property (that says if a product is zero, at least one of its factors must be zero): $$\begin{array}{rcl} x^4 + 2x^3 - 8x &=& 16\\ x^4 + 2x^3 - 8x - 16 &=& 0\\ x^3 (x+2) - 8(x+2) &=& 0\\ (x^3 - 8)(x+2) &=& 0 \end{array}$$Knowing that we can now solve where each factor on the left is zero with "socks and shoes", we need not completely factor the leftmost factor (which just happens to be a difference of cubes). Had one of the factors not been solvable with "socks and shoes", we might have continued trying to factor things further. Of course, a solution to either (smaller) equation will then solve the original equation: $$\begin{array}{rclcrcl} x^3 - 8 &=& 0 & \quad \textrm{ or } \quad & x + 2 &=& 0\\ x^3 &=& 8 & \quad \textrm{ or } \quad & x &=& -2\\ x &=& \sqrt[3]{8} & \quad \textrm{ or } \quad & x &=& -2\\ x &=& 2 & \quad \textrm{ or } \quad & x &=& -2\\ \end{array}$$Thus, $x = \pm 2$. |
As a final example, consider the solution to the following equation. Here, we use "socks and shoes" with the zero-product property, but only after a clever substitution to make the factorization needed for the zero-product property easier to identify and accomplish:
|
Question Solution Noting that $c^{2/3}$ is the square of $c^{1/3}$, we let $u=c^{1/3}$ and then rewrite the equation in terms of $u$, as shown below. (Note, we could work this problem without this substitution, but doing so makes it a bit harder to see each "next step" needed in its solution.) $$u^2 - u - 2 = 0$$Since we already have a zero on the right side, let us try to factor the left side and use the zero-product property: $$(u-2)(u+1) = 0$$ From here, we know one of the two factors on the left must be zero. As such, we quickly solve $u-2 = 0$ and $u+1=0$ with "socks and shoes" to find $u=2$ or $u=-1$. However, these are only solutions for $u$, not $c$. Remembering $c^{1/3} = u$, we can use our two solutions for $u$ to produce two more equations in terms of $c$, that we can again solve for with "socks and shoes": $$c^{1/3} = 2, \textrm{ so } \ c = 2^3 \quad \quad \textrm{ and } \quad \quad c^{1/3} = -1, \textrm{ so } \ c = -1$$ As such, $c = 8 \textrm{ or } c = -1$. |
Interestingly, this principle of undoing in reverse-succession the various functions applied to something can help us determine the graphs of certain functions as well!
The previous section argued how we might find the graph of a composition of certain simple functions with some function $g(x)$ whose graph is known. As as reminder, recall the "Important Side Comment" included in that section, shown again below:
An Important Side Comment: [...] we can find the graphs of such compositions as long as we know the graph of the inner-most function and the effect each function subsequently applied will have. For example, suppose we wanted to find the graph of $f(x) = -x^2 + 2$. Notice this is the composition of three functions: a vertical translation, a reflection over the $x$-axis, and $g(x) = x^2$ (whose graph we know). Specifically, if $g(x) = x^2$, $r(x) = -x$, and $t(x) = x+2$, then $f(x) = t(r(g(x)))$. As such, to find the graph of $f(x)$, we start with the graph of $g(x)$, the inner-most function; apply $r(x)$ by reflecting $g(x)$ over the $x$-axis; and then finally apply $t(x)$ by translating the resulting graph up $2$ units, as shown below. (Note: the graph $f(x)$ we seek is the one shown in bright red on the right): 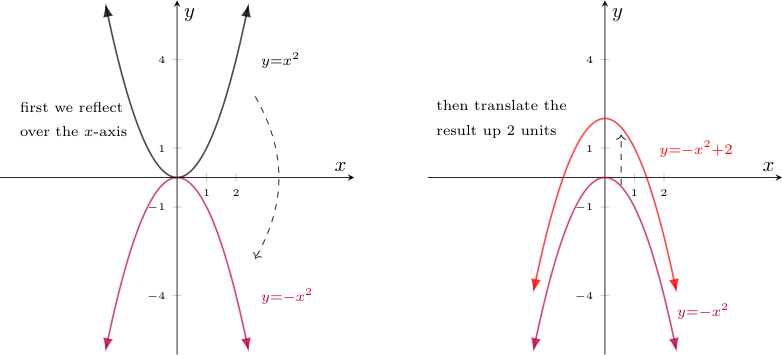 |
The example above applied two simple functions to $g(x)=x^2$, but there is of course nothing preventing us from doing something similar with more functions involved. So we can easily find the graph of $f_n(\cdots(f_2(f_1(g(x))) \cdots)$ if we know the graph of $g(x)$ and how each of the functions $f_1$, $f_2$, ..., $f_n$ transform graphs of functions with which they are composed.
However, now suppose we want to graph the function $h(x) = g(f_1(f_2(f_3(\cdots f_n(x)\cdots))))$, where the function $g(x)$ whose graph is known is now the outer-most function applied (instead of the inner-most).
Presuming each $f_i$ is invertible -- if we are lucky enough that $g(x)$ is also invertible†, finding this graph will be easy.
† : Usefully, even if $g(x)$ is NOT invertible, but can be defined in a piecewise way where each individual "piece" is invertible, the strategy about to be described will still work by applying it to each such piece!
Consider the inverse of $h(x)$. By "socks and shoes", we know $$h^{-1}(x) = f_n^{-1}(\cdots(f_2^{-1}(f_1^{-1}(g^{-1}(x))))\cdots)$$
Further, the graph of $g^{-1}$ is known as it is the reflection of the graph of $g(x)$.
As such, since one knows how $f_1^{-1}, f_2^{-1}, \ldots, f_n^{-1}$ will transform graphs to which they are applied given one knows how $f_1, f_2, \ldots, f_n$ transform graphs, we can apply the transformations related to the inverses of the $f_i$ functions in succession to the graph of $g^{-1}$ to find the graph of $h^{-1}(x)$.
Finally, we can reflect the graph of $h^{-1}(x)$ back across the line $y=x$ to find the graph of $h(x)$ originally desired.
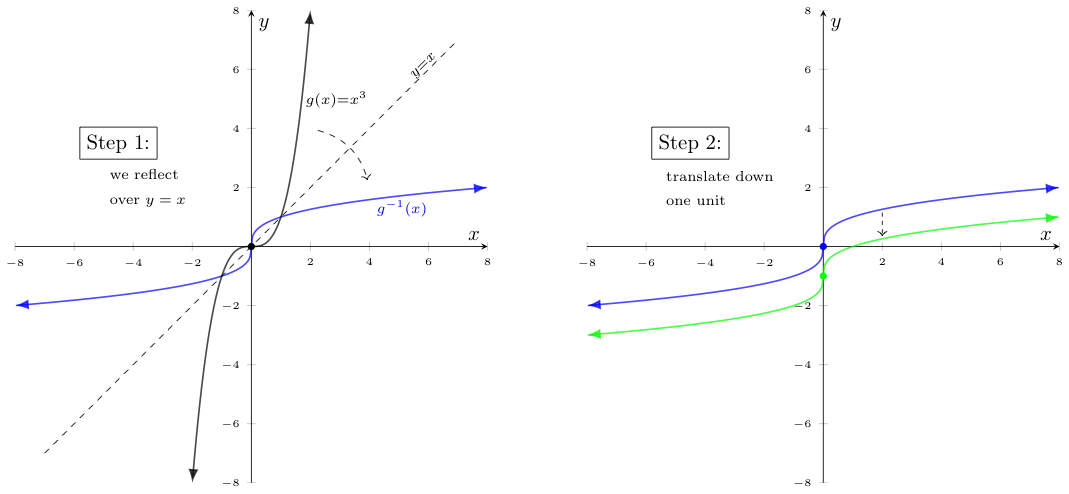
As an example, let us use this technique to find the graph of $h(x) = (-\frac{x}{2}+1)^3$.
Notice the outer function is $g(x)=x^3$, whose graph we know.
Also, we can express the inside of this function as a composition of several simple and invertible functions. Specifically, $-\frac{x}{2}+1 = f_1(f_2(f_3(x)))$, where $f_3(x) = -x$ (a reflection), $f_2(x) = \frac{1}{2}x$ (a vertical contraction), and $f_1(x) = x+1$ (a vertical translation upwards).
As such, we start with the graph of $g(x)$ reflected across the $y=x$ line (here, the graph of its inverse) and then apply the inverse transformations in reverse order. Specifically, we first apply $f_1^{-1} = x-1$ (a vertical translation downwards), then $f_2^{-1} = 2x$ (a vertical dilation), and then $f_3^{-1} = -x$ (another reflection), before finally reflecting the result over $y=x$ to find the graph of $h(x)$. The effects of these transformations are shown below:
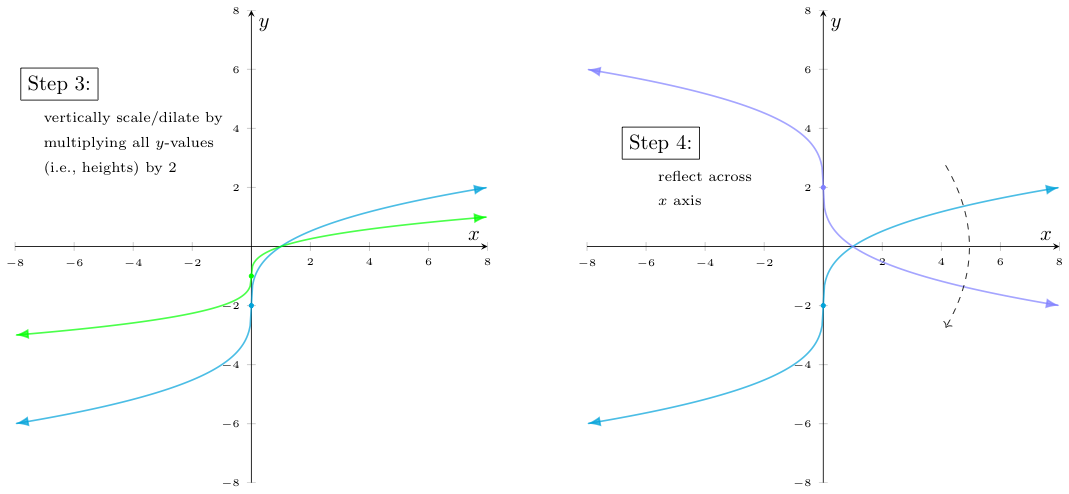
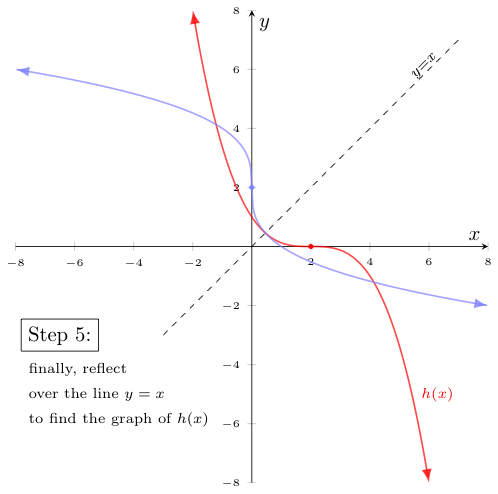
The method described above for graphing certain compositions of functions -- while easily justified with "socks and shoes" -- is not as efficient as it could be. It's not unlike if we wanted to write one's name backwards on a piece of paper and decided the best way to do that was to hold up our paper near a mirror, carefully write each letter of our name in sequence while looking at the reflection, and then pull the paper away from the mirror to examine the final result. Would it not be easier to just figure out how to write each letter backwards? Then we wouldn't even need the mirror!
In the above technique for graphing certain compositions, recall we invert a function, carefully apply each of our $f_i(x)$ transformations, and then invert the result to see the final result. In the same way would it not be easier to just figure out what effect the $f_i(x)$ functions have on $g(x)$? Then we wouldn't even need the first and last inversions!
The key to this is to realize that all of the $f_i(x)$ functions transform the graph to which they are applied in a vertical way (i.e., they change $y$-coordinates only). If we instead apply similar, but horizontal transformations directly to $g(x)$, we will accomplish the same result -- but without the need for the inversions.
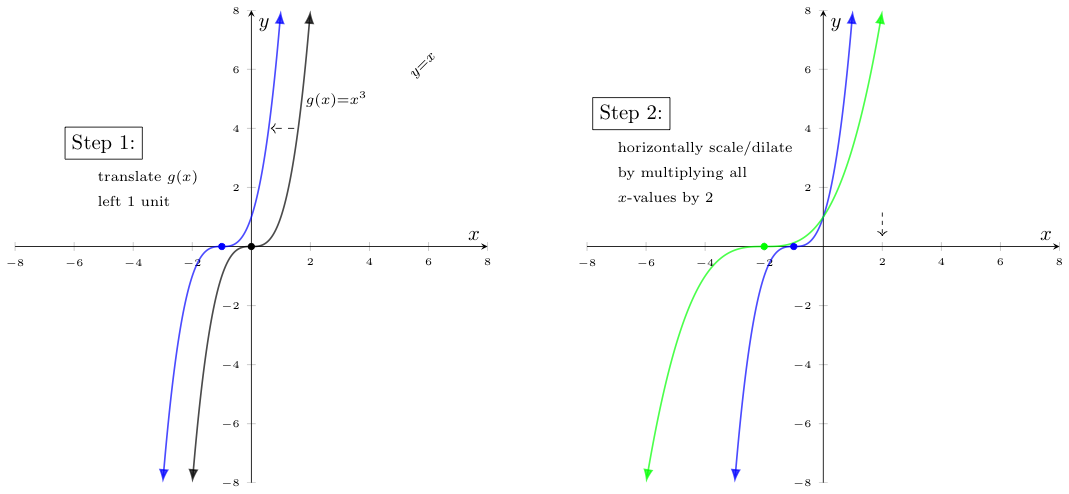
Let's make this more concrete with an example -- the same one worked out in a longer way above. Let us again graph $h(x) = (-\frac{x}{2} + 1)^3$:
Notice again that we can write $h(x)$ as a composition of an outer function $g(x)=x^3$, whose graph we know and several other simple and invertible functions. In particular -- and as before, $-\frac{x}{2}+1 = f_1(f_2(f_3(x)))$, where $f_3(x) = -x$ (a reflection), $f_2(x) = \frac{1}{2}x$ (a vertical contraction), and $f_1(x) = x+1$ (a vertical translation upwards).
Except this time, we will start with the graph of $g(x)$ and apply the inverse operations to $f_1$, $f_2$, and $f_3$, in that order -- but horizontally.
Specifically, with regards to:
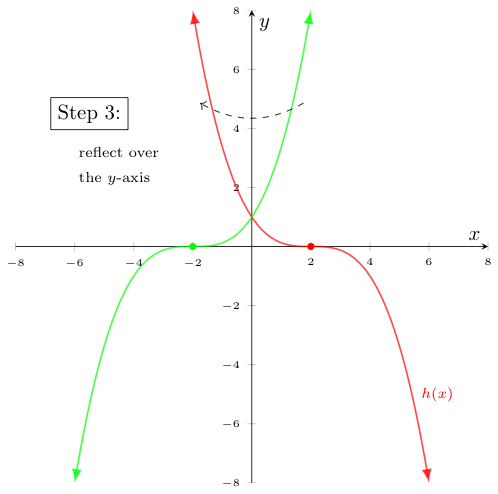
Notice we got to the same graph of $h(x)$ (in red) as we did before -- but in almost half the steps!
Not bad for a strategy inspired by footwear, eh?