| | |
Recall when we discussed the elimination of common factors seen in the numerator and denominator of a rational expression as a means for simplifying it, we took a moment to mention the importance of the domain in that process.
As a reminder, we were examining the following calculation which is true for values $x$ that make the left side defined: $$\require{cancel}\begin{array}{rcl} \cfrac{x^3 - 8}{x^2 - 5x + 6} &=& \cfrac{(x-2)(x^2 + 2x + 4)}{(x-2)(x-3)}\\ &=& \cancel{\cfrac{x-2}{x-2}} \cdot \cfrac{x^2 + 2x + 4}{x-3}\\ &=& \cfrac{x^2 + 2x + 4}{x-3} \end{array}$$ We contrasted this to the following functions, where we assume the implicit domain for each. $$f(x) = \frac{x^3 - 8}{x^2-5x+6} = \frac{(x-2)(x^2+2x+4)}{(x-2)(x-3)} \quad \quad \textrm{and} \quad \quad g(x) = \frac{x^2 + 2x + 4}{x-3}$$ Because the domain of $g$ is defined at $x=2$, but $f$ isn't, we deduced these functions are not equal.
Let's run with this idea a bit. Since these two functions have different domains, their graphs should be different, right? What does the graph of $f$ look like?
Suppose we try to use a graphing calculator to get a quick plot of $y=f(x)$. Sadly, doing so is rife with problems. Here's what we will see using the default viewing window on a TI-89 calculator:
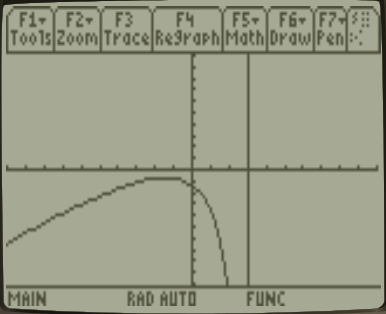
Let's step through the issues with the above, one by one:
First, we see what appears to be a vertical line at $x=3$ in our graph. That can't be, as then $f$ wouldn't even be a function! Recall that a truly vertical line there would tell us that there are infinitely many $y$ values associated with $x=3$. On the contrary, given what we know about how the denominator factors in $f(x)$ we expect that there shouldn't be any $y$-values associated with $x=3$, as $f(x)$ is undefined there!
Second, there is nothing shown to the right of $x = 3$, suggesting that either our domain does not include $x \gt 3$ or that we haven't found a window where we can see the points for these $x$-values presuming they exist. As it turns out, the latter case captures what is truly happening and there are actually more points on the graph of $y=f(x)$ above $y=8+2\sqrt{19} \approx 16.7178$. To discover these other points exist, we could of course play with the $x$ and $y$ ranges in the calculator, hoping to see more of the function. For example, if we expand things to include $-20 \lt y \lt 20$, we'll see the aforementioned points at the top right.
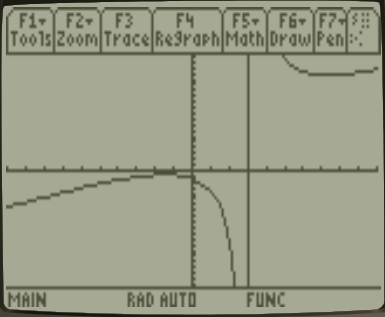
That seems like a reasonable thing to do -- but what if the missing points were above $y=3000$ instead of $y=16.7178$? One might easily have given up looking before finding where these points lie. Further, how is it that we can even determine the first $y$ value above what we initially plotted is $8+2\sqrt{19}$? The square root tells us the value with infinite precision -- which most simple calculators simply can't provide.
Third, even if we zoom out a bit as we did above, the graph appears to have a point plotted at $x=2$. However, we know better! Again looking at the factorization of the denominator in $f(x)$, this function should not be defined at $x=2$, since it would create a division by zero!
Of course the issues explored above are no surprise. Recall the Caveat Calculatus section of our previous discussion on functions, which explains why these things occur and encourages us to be wary of trusting calculators to always tell us the truth (they don't).
Still, we want to be able to detect when our calculators are lying to us. We want to know where the different parts and interesting features of functions' graphs are going to be. We want to know where we should expect points on those graphs to exist and where they won't. In short, we want to be able to create graphs of functions that actually reflect what is really going on, like the one shown below for $f(x)$:
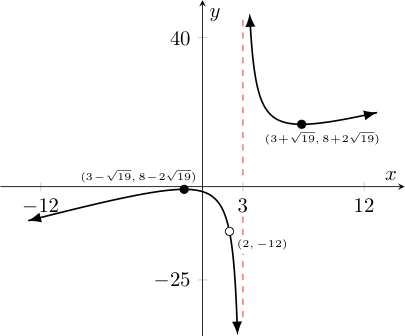
Note how much clearer all the interesting features are in the above graph!
In particular note how we have:
Calculus will help us find several of these interesting features, and thus help us create these much better representations of graphs of functions -- notably without technology (i.e., just via some hand calculations)!
For example, it is calculus that reveals the peculiar coordinates where the aforementioned minimum and maximum $y$-values occur; it is calculus that reveals where a function increases/decreases as its $x$-values grow; it is calculus that reveals even where the function "cups upwards"or "cups downwards".
In the case of polynomial and rational functions, all of revelations just described will be connected to the single task of finding where polynomials are zero! Even beyond calculus there is important information about functions and their graphs that can be gleened from knowing where certain polynomials are zero.
For example, we can find the implicit domain of a rational expression in one variable by determining where the polynomial in its denominator is zero.
Likewise, being able to find where a rational expression's numerator polynomial is zero and its denominator polynomial is not, reveals the $x$-intercepts associated with its graph. You may recall that an $x$-intercept is a place where the graph of a function crosses the $x$-axis.
(Interestingly -- for the function discussed above -- we can show the numerator is never zero when the denominator is not zero. As such, there are no $x$ intercepts to find for this particular function.)
We can even find where one polynomial or rational function crosses another and which one is above the other elsewhere, by finding where certain polynomials are zero. This includes finding where a polynomial or rational function lies above or below the $x$-axis, and hence where such a function is positive or negative in value.
With so many applications, finding where polynomials (of a single variable) are zero will be at the root of a whole lot of things we will want to do. With this in mind, we say that the values of $x$ where a polynomial function $p(x)$ equals zero are the roots of the polynomial, p(x).† We also sometimes call these the zeros of the polymomial.
We sometimes further distinguish these as rational roots or real roots when they are rational or real values, respectively.
Notably, when the polynomial is easily factored into factors of degree one, determining the roots is immediate.
As an example, consider the following polynomial and its factorization: $$2x^3-7x^2-120x+189 = (2x-3)(x+7)(x-9)$$
If we seek the roots of this polynomial, we then must solve $$2x^3-7x^2-120x+189 = 0$$ or equivalently, given the factorization just found: $$(2x-3)(x+7)(x-9) = 0$$ To do this, recall real numbers enjoy the following property:
|
Zero Product Property: The product of two non-zero elements is non-zero, which implies if $ab = 0$, then either $a=0$ or $b=0$. |
As such, to find the roots, we can simply solve the related equations. For the above example, we would need to solve $$2x-3 = 0, \quad \quad x+7 = 0, \quad \textrm{ and } \quad x-9=0$$ These quickly reveal the roots of $2x^3 - 7x^2 - 120x + 189$ to be $x=3/2$, $-7$, and $9$.
Sometimes of course, factoring a polynomial is hard. For example, could you have factored the above cubic polynomial if it had not been done for you?
This sets up one of the bigger problems this course will consider. When given a polynomial (especially one with a high degree), whose factorization is hard (or impossible) to find, what can we say about the nature or existence of its roots?
We will tackle this problem soon enough. However, before doing so, let us consider some examples of the (non-calculus based) applications mentioned that were related to finding roots of polynomials -- especially for expressions involving easily factorable polynomials.
† : The word "root" has a double meaning here. On the one hand, finding these values forms the basis of much that we will want to do. (Recall in Latin, the word radix means both "root" and "basis".) On the other, we will see that sometimes roots of some simple polynomials are expressible as square roots, cube roots, fourth roots, etc. of some value. For example, $x^2 - 5$ equals zero precisely when $x = \pm\sqrt{5}$.
Suppose we wish to know the implicit domain of the following function: $$f(x) = \frac{x+2}{x^2 + 7x + 10}$$ As the numerator and denominator (being polynomial functions) can always be evaluated at any given $x$, we see that the only thing that could result in $f$ being undefined is if the denominator was zero.
As such, we need to know where $x^2 + 7x + 10 = 0$ since these $x$-values are precisely the ones that need to be excluded from the implicit domain of the function defined by this above.
Note the denominator can be easily factored: $$f(x) = \frac{x + 2}{(x+2)(x+5)} $$ As such, we solve $x+5 = 0$ and $x+2 = 0$ to find $x=-5,-2$ are the values that will make $f$ undefined.
Thus, $$\textrm{implicit domain of } f = \{x \in \mathbb{R} \ | \ x \neq -5,-2\}$$ Note, one should avoid the temptation to "cancel" the $(x+2)$ factor -- as doing so creates a new function with a different implicit domain.
Suppose we seek the $x$-intercepts associated with the rational function $$f(x) = \frac{-2x^2 -2x + 12}{x^3 -7x^2 -4x + 28}$$ Factoring both the numerator and the denominator, we find $$f(x) = \frac{-2(x-2)(x+3)}{x^2(x-7) - 4(x-7)} = \frac{-2(x-2)(x+3)}{(x^2-4)(x-7)} = \frac{-2(x-2)(x+3)}{(x-2)(x+2)(x-7)}$$ Given this factorization, notice the polynomial in the numerator is zero when $x-2 = 0$ or $x+3 = 0$, or equivalently when $x=2$ or $x=-3$.
However, we should also notice that the factorization of the denominator tells us that of these two values, $f$ is not defined at $x=2$ as otherwise the factor $(x-2)$ and hence the value of the entire denominator, by which we are dividing, is zero!.
Since $f$ can't have an $x$-intercept at a value where it is undefined, that leaves $f$ having an $x$-intercept only at $x=-3$.
Starting with the easier of the two, suppose we wish to know where the following function is positive and where it is negative: $$f(x) = x^3 - 2x^2 - 9x + 18$$ If we can factor $f$ so that we know exactly where the individual factors are positive, negative, or zero -- then determining where $f(x)$ is positive, negative, or zero will be easy.
In this case, notice that $$f(x) = x^2(x-2) - 9(x-2) = (x^2-9)(x-2) = (x+3)(x-3)(x-2)$$ Now we turn attention to where each of these factors is individually positive, negative or zero. Each factor contributes a zero, of course (recall the Factor Theorem presented at the end of our previous discussion on polynomial division). Consider first the factor $(x+3)$. Noting that "being positive" is identical to "being greater than zero", we look for $x$ values where $x+3 \gt 0$. Equivalently, $x \gt -3$. This leaves the rest of the values of $x$ to be negative. We can summarize these three facts with the following image.
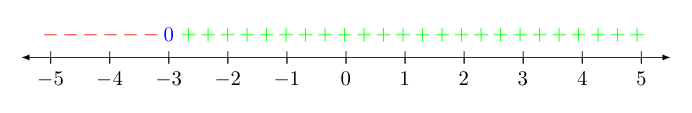
Similarly, the factor $(x-3)$ is positive $x \gt 3$, and $(x-2)$ is positive when $x \gt 2$. Noting when these factors are also $0$ and the remaining $x$ values that make each factor negative, we summarize what we know about these two other factors with the images below:
Stacking these together, it is easy to see when their product (and hence, $f$) is positive, zero, or negative.
Anywhere there is a zero, $f$ has a root. Anywhere else associated with an even number of negative factors is positive, and the remaining places (with an odd number of negative factors) must be negative.
So above, $f$ is zero at $x = \pm 3$ and $x = 2$, positive in $(-3,2) \cup (3,\infty)$, and negative in $(-\infty,-3) \cup (2,3)$.
Now let's consider what happens when a rational expression is involved. Suppose $f$ is defined by $$f(x) = \frac{x^4-5x^3+6x^2}{-x^3 + 3x^2 - x + 3}$$ and we wish to know where $f$ is above or below the $x$-axis. As before, we start by fully factoring the function given: $$f(x) = \frac{x^4-5x^3+6x^2}{-x^3 + 3x^2 -x +3} = \frac{x^2(x-2)(x-3)}{-x^2(x-3)-(x-3)} = \frac{x^2(x-2)(x-3)}{(-x^2-1)(x-3)} = \frac{x^2(x-2)(x-3)}{-(x^2+1)(x-3)}$$ Considering the contribution of each factor found:
Notice $f(x) = 0$ when either $x=0$ or $x=2$. However $f(x)$ is undefined at $x=3$, as the denominator is zero there. One should be aware that being undefined and the the acronym "D.N.E." which stands for does not exist are often used interchangeably.
The factor $(x-2)$ is positive when $x \gt 2$, while the factor $x^2$ is positive when $x \neq 0$.
However, $(x-3)/(x-3) = 1$ for every $x \neq 3$, so this portion of the rational expression won't affect the sign ($1$ is positive) anywhere it exists.
Also, $(x^2+1)$ is the sum of a value always greater than or equal to zero (i.e., $x^2$) and a positive value, and must therefore always be positive. Another way to see this is to note that $y = x^2 + 1$ would have solutions corresponding to the points on the graph of $y = x^2$, but shifted up one unit -- so that the $y$-values are always positive.
Sneakily, there is an additional factor of $-1$ in the front of the denominator. This additional factor will affect the sign of the whole function, so we must not forget its contribution!
Putting all this information together on one number line so that we can do the sign analysis, we get the following:
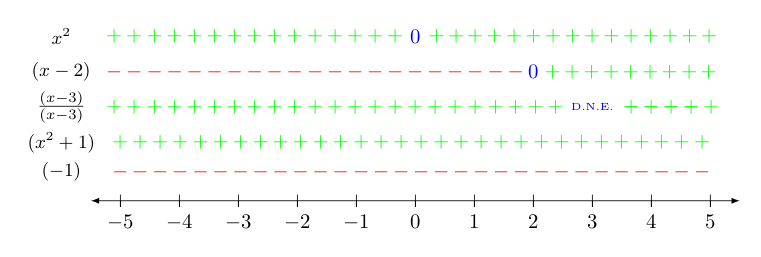
The above makes it clear that $f(x)$ is zero when $x = 0$ or $x = 2$, undefined when $x=3$, positive (and hence, above the $x$-axis) when $x$ is in $(-\infty,0) \cup (0,2)$, and negative (and hence, below the $x$-axis) when $x$ is in $(2,3) \cup (3,\infty)$.