

 |  |
We have now seen several ways to combine two things of some type to produce something else of the same type.$\require{newcommand}$
In mathematics, we often represent this combination using some special operator symbol like $+,-,\times,\cdot,*,$ or $\div$, placing such symbols between the expressions for the two things being combined (which are called operands), in a manner consistent with the following:
$$2+3, \quad 4-x, \quad a \times b, \quad x \cdot y, \quad B_1 * B_2, \quad 8 \div 2$$Other notations throw in special positioning in accomplishng the same thing. For example, in the calculation of a power the first operand is written first, with the second generally written smaller, as a superscript to the first. As another, quotients (when expressed as a fraction) put their first operand above their second operand, separated by a horizontal bar, while products can also be expressed by putting the operands side-by-side, with no operator in between, as the following suggest: $$x^5, \quad \frac{a}{b}, \quad 3y$$
Each notation has its own interesting history and evolution. For example:
The plus sign "$+$" seems to have stemmed from an abbreviated form of "et" which in Latin means "and".
The use of the dot "$\cdot$" to signify multiplication is directly attributable to G.W. Leibniz, co-founder of calculus, who wrote in a letter to John Bernoulli in 1698: "I do not like $\times$ as a symbol for multiplication, as it is easily confounded with $x$; ...often I simply relate two quantities by an interposed dot".
H.T. Colebrooke (1765-1837), an English mathematician and student of Asian cultures, tells us that the vertical positioning of values divided to form a fraction can be traced back to Hindu algebraists, except without the line of separation (which seems to have been introduced sometime in the 15th century). A similar notation for unit fractions (i.e., fractions of the form $1/n$) is used in the Rhind Papyrus, one of the oldest known mathematical documents, written by Egyptian scribe Ahmes -- who in turn claims what he wrote comes from an earlier work of about 2000 BC.
Let us put aside our discussion of notation just for a moment though. Instead, let us focus on how all of the above represent combinations of two things to produce a third.
When we write $a^b = c$, we can think about this as combining the values of $a$ and $b$ to get $c$. Indeed, finding that value $c$ when $a$ and $b$ are known is what we mean when we evaluate the power.
However, what if we only knew the values of $b$ and $c$? Could we not somehow determine the value of $a$? For example, if you knew for some unknown real value $x$ that $x^3 = 64$, could we not deduce somehow that the value of $x$ that makes this true is $4$?
We can of course say that $x=4$ is the solution to (or more briefly "solves") the equation $x^3 = 64$, but there is another way to look at this:
If we changed either the $3$ or the $64$ above, the solution for $x$ would certainly change. In this sense, we can see the solution depends on both of these values (and only these two values) -- that is to say, the solution can be thought of as some strange "combination" of these two values...
Do you see where this is leading? Maybe we should create some new notation to represent this new type of combination of two values!
The true history of one notation we use to specify this combination is hard to nail down, but the following has been put forth by others (see Cajori, 1928) as a plausible explanation:
Remember that if $x^y=z$, we call $x$ the base, $y$ the exponent, and $z$ the value of the power that results. So the value we seek above is the base for a (third) power. In Latin, the word for "basis" can be expressed as either "radix" or "radic" (with both of these also meaning "root").
Given that "radix", "radic", and "root" all start with an $r$, perhaps -- as a first pass -- we could use that letter to represent the mysterious "base" $x$ that makes $x^3 = 64$ true by writing $x = 3 \; \textrm{r} \; 64$". Not much imagination is required to see how this might evolve over time into "${}^{3} \surd \, 64$".
Of course, this notation will cause confusion if the power (here, $64$) is anything more complicated than a single number or variable.
For example, how should we denote the base/root $x$ where $x^3 = y+1$?
Writing the following is going to be confusing: $${}^{3} \surd \, y + 1$$ One might interpret this to mean a value which raised to the third power results in $y+1$ (what we desired). Alternatively, one might see this as the sum of two things: a value which raised to the third power results in $y$, and the value $1$? It's not clear!
We need to indicate with our notation somehow that the evaluation $y+1$ should be done first, followed by the evaluation of the $\surd$. The modern solution for this would be to group the $y+1$ inside parentheses, yielding $${}^{3} \surd \, (y + 1)$$ However, this isn't the only way we could proceed. Another way things can be "grouped together" is by drawing above them a horizontal line, called a vinculum (a Latin word meaning "to fetter, chain, or tie"). If we use this technique, we end up with $${}^{3} \surd\,\overline{y+1}$$ This is exactly what René Descartes did in 1637, which of course morphed into a notation still used today: $$\sqrt[3]{y+1}$$
As a matter of verbiage -- and again connecting to the Latin word "radic" -- we say the expression $\sqrt[n]{x}$ is written in radical notation, identifying $n$ as the index and $x$ as the radicand.
To preserve the ink in our pens -- and similar to how we tend not to write $x^1$ very often, but only $x$ instead -- when the index is $2$, we omit writing the index at all (i.e., we define $\sqrt{x} = \sqrt[2]{x}$).
There is one more wrinkle that needs addressing, though. We know for example, that both $3^2 = 9$ and $(-3)^2 = 9$. So which should we mean when we write $\sqrt{9}$? Should this be $3$ or $-3$? More generally, what should we do when the index is even and the real value we seek is not unique?
With this question in mind, we make the following definition:
Note that when the index $n$ is even and the radicand $y$ is negative, there is no real value equal to $\sqrt[n]{y}$.
Also, when the index $n$ is even and the radicand $y$ is positive, there are two real $n^{th}$ roots of $y$, given by $$\sqrt[n]{y} \quad \textrm{ and } \; -\sqrt[n]{y}$$
Italian mathematician, Giuseppe Peano in his book Formulaire des Mathematiques, gives us another notation that we can (and will) use to denote the set of all $n^{th}$ roots of $y$, that will make a later argument we address much prettier: $$\sqrt[n]{{}^* y}$$
While some roots are rational (e.g., $\sqrt{9} = 3$, $\sqrt{4/25} = 2/5$, etc.) in the sense that they can be written as a ratio/quotient of two integers, most are irrational (i.e., not rational). Strangely however, how we know certain roots are irrational is often withheld from students. The author finds this sad, as the logic behind these claims is not complicated -- in fact, its quite beautiful. Fortunately for any readers previously denied such exposure -- your time has come!
Suppose we wish to argue that $\sqrt{2}$ is irrational. We will do so indirectly. That is to say, it either is irrational or it isn't. If we can show the latter leads to something ridiculous being true, then it must be the former that is correct.With that in mind, let us suppose that $\sqrt{2}$ is not irrational. Then, we should be able to find some fraction $a/b$ of two integers $a$ and $b$ which $\sqrt{2}$ equals. Indeed, if such a fraction exists, we can always reduce it to lowest terms $p/q$ so that $$\sqrt{2} = \frac{p}{q} \quad \quad \textrm{where $p$ and $q$ share no common factor}$$ Now suppose we square both sides, finding $$2 = \frac{p^2}{q^2}$$ and then multiply both sides by $q^2$ to get rid of the fraction: $$2q^2 = p^2$$ As both $p$ and $q$ are integers, it must be the case that $p^2$ (and hence $p$) is even, right?
Consequently, we can find some integer $k$ so that $p=2k$. But then, $$2q^2 = 4k^2$$ Dividing both sides by $2$ we have $$q^2 = 2k^2$$ which likewise suggests $q^2$ (and hence $q$) is even as well.
However, this is impossible! Recall $p/q$ was a fraction in lowest terms, so $p$ and $q$ can't both be even!
As the assumption that $\sqrt{2}$ was rational (and thus writable as a fraction of integers) led to a contradiction, that can't be the case. There is only one other option left -- $\sqrt{2}$ is irrational!
Initially, recall that we defined $y^n$ to be the product of $n$ values of $y$ multiplied together. However, this definition didn't make much sense if $n$ was $0$ or negative.
Still, there were useful ways to define zero and negative powers that were consistent with the exponent rules we discovered. (i.e., $y^0 = 1$ and $y^{-n} = 1/y^n$).
Knowing full well that something like $y^{1/3}$ makes no more sense in terms of that original definition then did $y^0$ or $y^{-3}$, is there a way that we could define it anyways, so that it would be consistent with our other exponent rules?
In particular, recall the rule that tells us when finding a power of a power, we multiply the exponents. By that rule, shouldn't this be true? $$(y^{1/3})^3 = y^{(1/3)\cdot 3} = y^1 = y$$
Notice that this means when $y=64$: $$(64^{1/3})^3 = 64$$ Do you see how $x=64^{1/3}$ would then solve $x^3=64$?
But that means that $64^{1/3}$ will -- if it is to have any meaning at all -- must equal $\sqrt[3]{64}$!
With this as motivation, we define the expression $y^{1/n}$ (for any real value $y$ and integer $n$) to be the same thing as $\sqrt[n]{y}$, calling this rational exponent notation.
As one can see, we now have two competing notations for the exact same thing -- and BOTH are used throughout modern-day mathematics!
"Why?", you undoubtedly ask...
You can thank René Descartes. You see, when Descartes added the vinculum to make a better functioning radical notation, he did so sadly after two other mathematicians (Nicole Oresme and Simon Stevin) had already advanced the (much better) idea of fractional exponents. As Swiss-American historian of mathematics, Florian Cajori writes:
"[If Descartes had only] discarded the radical sign ...it is conceivable that generations upon generations of pupils would have been saved the necessity of mastering the operations with two difficult notations when one alone (the exponential) would have answered all purposes. But Descartes missed this opportunity, as did later also I. Newton who introduced the notation of the fractional exponent, yet retained and used radicals." -- Cajori
Alas, as the saying goes: there's no use crying over spilt milk. We have these two notations -- we might as well make friends of them.
Note that the latter notation does have a wonderful consequence of allowing us to easily generalize powers to include exponents that take the form of any fraction -- not just recipricals of the form $1/n$.
Just consider the results of applying the rule about multiplying exponents when finding powers of powers as it relates to $(x^{1/n})^m$ and $(x^m)^{1/n}$ for any two integers $m$ and $n \ne 0$.
We'll clearly want to define $x^{m/n}$ so that $$\sqrt[n]{x^m} = (x^m)^{1/n} = x^{m/n} = (x^{1/n})^m = (\sqrt[n]{x})^m$$
Not surprisingly, since radical notation and rational exponent notation are just two different ways of expressing the same things, there is great deal of interplay between these two notations. Proving results for one immediately gives us results for the other. For example, we can deduce the following rules for radicals from what we know about exponents:
We know $(xy)^{1/n} = x^{1/n} y^{1/n}$, so it must also be the case that
$$\boxed{\sqrt[n]{xy\vphantom{l}} = \sqrt[n]{x\vphantom{y}} \sqrt[n]{y\vphantom{l}}}$$Similarly, given that $\displaystyle{ \left( \frac{x}{y} \right)^{1/n} = \frac{x^{1/n}}{y^{1/n}}}$, we have
$$\boxed{\displaystyle{\sqrt[n]{\frac{x}{y}} = \frac{\sqrt[n]{x}}{\sqrt[n]{y}}}}$$Lastly, given that $\displaystyle{ \left( x^{\frac{1}{n}} \right)^{\frac{1}{m}} = x^{\frac{1}{n} \cdot \frac{1}{m}} = x^{\frac{1}{mn}}}$ we see that $$\boxed{\displaystyle{\sqrt[m]{\sqrt[n]{x}^{\phantom{1}}} = \sqrt[m n]{x}}}$$
We have already spoken to some considerations to keep in mind when simplifying expressions involving exponents. When these exponents are rational values (i.e., fractions) little changes.
When dealing with simplifying expressions involving radicals, a few conventions will both help keep the variability of how we write equivalent expressions to a minimum, and generally makes approximating its value easier:
Some examples of using the above rules to simplify radical expressions follow. As with exponents, there are often multiple valid paths to an expression's simplified form. Often, one will find it useful to translate from radical form to rational exponent form first, simplify the resulting expression, and then rewrite things back in radical form, as the first example below demonstrates:
Simplify $\displaystyle{\cfrac{\sqrt{x^7 y^8}}{\sqrt[4]{x^2 y z^6}}}$, presuming $x$, $y$, and $z$ are positive real values
$\require{mathtools}$ $$\begin{array}{rcl} \displaystyle{\cfrac{\sqrt{x^7 y^8}}{\sqrt[4]{x^2 y z^6}}} &=& \displaystyle{\cfrac{(x^7 y^8)^{1/2}}{(x^2 y z^6)^{1/4}}} \leftarrow {\scriptstyle \textit{translate to rational exponents notation}}\\\\ &=& \displaystyle{(x^7 y^8)^{1/2} (x^2 y z^6)^{-1/4}}\\\\ &=& \displaystyle{x^{7/2} y^4 x^{-1/2} y^{-1/4} z^{-3/2}}\\\\ &=& \displaystyle{x^3 y^{15/4} z^{-3/2}}\\\\ &=& \displaystyle{x^3 y^3 y^{3/4} z^{-2} z^{1/2}} \quad \leftarrow {\scriptstyle \textit{see comment below}}\\\\ &=& \displaystyle{x^3 y^3 z^{-2} y^{3/4} z^{2/4}} \quad \leftarrow {\scriptstyle \textit{so corresponding radicals in the next step will combine}}\\\\ &=& \displaystyle{x^3 y^3 z^{-2} \sqrt[4]{y^3} \sqrt[4]{z^2}}\\\\ &=& \displaystyle{\cfrac{x^3 y^3 \sqrt[4]{y^3 z^2}}{z^2}} \end{array} $$
Note in the fifth line above, we pulled the powers of both $y$ and $z$ apart so that each had an integer power present and a "remainder" power where the exponent is positive, fractional, and less than $1$. This is similar to writing a fraction in "mixed-numeral" form. Doing so accomplishes two things: It keeps us from having to pull any $n^{th}$ powers out from under an $n^{th}$ root expressed with a radical, when we translate back to that form. It also ensures there are not radicals left in the denominator.
Simplify $\sqrt[3]{x^2\sqrt{x^7 y^6 z^5}}$, presuming $x$, $y$, and $z$ are positive real values
$$\begin{array}{rcl} \sqrt[3]{x^2\sqrt{x^7 y^6 z^5}} &=& (x^2 (x^7 y^6 z^5)^{1/2})^{1/3}\\\\ &=& (x^2 x^{7/2} y^3 z^{5/2})^{1/3}\\\\ &=& (x^{11/2} \, y^3 \, z^{5/2})^{1/3}\\\\ &=& x^{11/6} \, y \, z^{5/6}\\\\ &=& x \, x^{5/6} \, y \, z^{5/6} \quad \leftarrow {\scriptstyle \textit{pulling powers apart again (for the same reason)}}\\\\ &=& x y \, \sqrt[6]{x^5} \, \sqrt[6]{z^5} \\\\ &=& xy \sqrt[6]{x^5 z^5} \end{array}$$
Simplify $\displaystyle{\frac{2\sqrt{x}}{\sqrt[5]{y^8 z}}}$, presuming $x$, $y$, and $z$ are positive real values.
If we didn't care about avoiding radicals in the denominator (and sometimes we don't) then replacing $\sqrt[5]{y^8 z}$ in the denominator above with $y^{8/5} z^{1/5} = y \cdot y^{3/5} z^{1/5} = y (y^3 z)^{1/5} = y \sqrt[5]{y^3 z}$ would suffice.
However, if we want to write this without any radicals in the denominator and at most a single radical in the numerator (which is always possible), we'll need a clever multiplication...
$$\begin{array}{rcl} \cfrac{2\sqrt{x}}{\sqrt[5]{y^8 z}} &=& \cfrac{2 x^{1/2}}{(y^8 z)^{1/5}}\\ &=& \cfrac{2 x^{1/2}}{y^{8/5} z^{1/5}} \quad \leftarrow {\scriptstyle \textit{without doing something, we're about to have radicals left in our denominator!}}\\ &=& \cfrac{2 x^{1/2}}{y^{8/5} z^{1/5}} \cdot \cfrac{y^{2/5} z^{4/5}}{y^{2/5} z^{4/5}} \quad \leftarrow {\scriptstyle \textit{trick: multiply by a well-chosen value of $1$ that makes the denominator's exponents integers}}\\ &=& \cfrac{2 x^{1/2} y^{2/5} z^{4/5}}{y^2 z}\\ &=& \cfrac{2 x^{5/10} y^{4/10} z^{8/10}}{y^2 z} \quad \leftarrow {\scriptstyle \textit{getting common denominators for the exponents gives us just one radical in the next step!}}\\ &=& \cfrac{2\sqrt[10]{x^5 y^4 z^8}}{y^2 z} \end{array}$$ You can see the "simplified form" here -- because of the extra work to eliminate the radicals from the denominator -- actually looks a bit more complicated than the expression with which we started. Alas, this is the cost sometimes!Simplify $\sqrt{x^2}\sqrt[3]{y^3}\sqrt{z^4}$
We have no presumption that $x$, $y$, and $z$ are positive values here, so we must be careful. Note that $x^2$ is always positive, so $\sqrt{x^2}$ will indeed produce a real root -- but it is the principle root associated with a radical that has an even index, and hence must be positive. We can ensure this is the case by using absolute value: $\sqrt{x^2} = |x|$.
The second factor $\sqrt[3]{y^3}$ is less problematic. We don't need to worry about forcing things positive since we have an odd index. This quickly simplifies to $\sqrt[3]{y^3} = (y^3)^{1/3} = y^1 = y$.
The third factor $\sqrt{z^4}$ again involves a principle root whose radical has an even index and hence must also result in a positive value. However, as $(z^4)^{1/2} = z^2$ is already positive by virtue of the squaring, an additional absolute value to force the issue is not necessary.
All this taken together, we can simplify the above to the following: $$\sqrt{x^2}\sqrt[3]{y^3}\sqrt{z^4} = |x|yz^2$$
Simplify $(\sqrt[3]{x} + 2)(\sqrt[3]{x^2} - 2\sqrt[3]{x} + 4)$
Don't forget that in the real numbers, multiplication distributes over addition. That is to say, for any real values $a$, $b$ and $c$ we know that $a(b+c) = ab + ac$ and $(b+c)a = ba + ca$.
More generally, by repeated applications of this property one can show that something similar holds when adding more than just two terms. Essentially, for any real values $a$, $b_1$, $b_2$, $b_3$, ..., $b_n$: $$a(b_1 + b_2 + b_3 + \cdots + b_n) = ab_1 + ab_2 + ab_3 + \cdots ab_n$$ $$(b_1 + b_2 + b_3 + \cdots + b_n)a = b_1 a + b_2 a + b_3 a + \cdots b_n a$$ Applying the these to our expression and noticing a couple of convenient cancellations yields $$\begin{array}{rcl} (\sqrt[3]{x} + 2)(\sqrt[3]{x^2} - 2\sqrt[3]{x} + 4) &=& (\sqrt[3]{x} + 2)\sqrt[3]{x^2} + (\sqrt[3]{x} + 2)(-2\sqrt[3]{x}) + (\sqrt[3]{x} + 2)4\\ &=& \sqrt[3]{x}\sqrt[3]{x^2} + 2\sqrt[3]{x^2} -2(\sqrt[3]{x})^2 -4\sqrt[3]{x} + 4\sqrt[3]{x} + 8\\ &=& \sqrt[3]{x^3} + 2\sqrt[3]{x^2} - 2\sqrt[3]{x^2} - 4\sqrt[3]{x} + 4\sqrt[3]{x} + 8\\ &=& \sqrt[3]{x^3} + (2\sqrt[3]{x^2} - 2\sqrt[3]{x^2}) + (-4\sqrt[3]{x} + 4\sqrt[3]{x}) + 8\\ &=& \sqrt[3]{x^3} + 0 + 0 + 8\\ &=& x + 8 \end{array}$$ That's a surprisingly simple answer for what initially appeared as a potentially "gross-looking" problem -- don't you agree? 😀
Much of the above focuses on how to denote and manipulate various roots, but avoids their calculation.
Strangely, this is often the case when students are introduced to radicals and rational exponents. Still -- that doesn't seem right, does it?
Recall, when calculating the value of a constant $c$ raised to some positive integer $n$, we just multiply $c$ by itself over and over again, a total of $n$ times to find $c^n$. Interestingly, an ancient method known to the Babylonians for calculating $\sqrt{c}$ also involves a simple calculation done over and over.
Even better -- with a little modification to this technique, we can find $\sqrt[n]{c}$ for any integer $n \gt 2$ as well!:
Suppose we wish to find $\sqrt{c}$ for some positive real value $c$. For example, suppose we are interested in finding the square root of $c=2$. We might make some initial guess to its value. Here, $1$ is clearly too small and $2$ would be too big, so maybe a good initial guess is $x_1=1.5$.
Now, think about the size of $x_1$ as it relates to the size of the quotient $\frac{c}{x_1}$.
One of two things must happen: Either our guess $x_1$ is smaller than $\sqrt{c}$ and this quotient $\frac{c}{x_1}$ is bigger than $\sqrt{c}$, or $x_1$ is bigger and $\frac{c}{x_1}$ is smaller. (Why?).
Regardless, we have trapped the square root we seek between $x_1$ and $\frac{c}{x_1}$. What's more -- this square root, $\sqrt{c}$, is the geometric mean of these two values!
In case one's recollection of what the geometric mean represents is rusty -- there are multiple different kinds of "means" in mathematics. The arithmetic mean (AM) of $a$ and $b$ is just their average $AM = \frac{a+b}{2}$. The geometric mean (GM) of $a$ and $b$ is calculated in a similar way, but instead of adding we multiply, and instead of dividing by $2$ we take a square root: $GM = \sqrt{ab}$.
Interestingly, the geometric mean of two positive values can never be greater than their arithmetic mean, as the ambitious reader might deduce from the "proof without words" image given below.
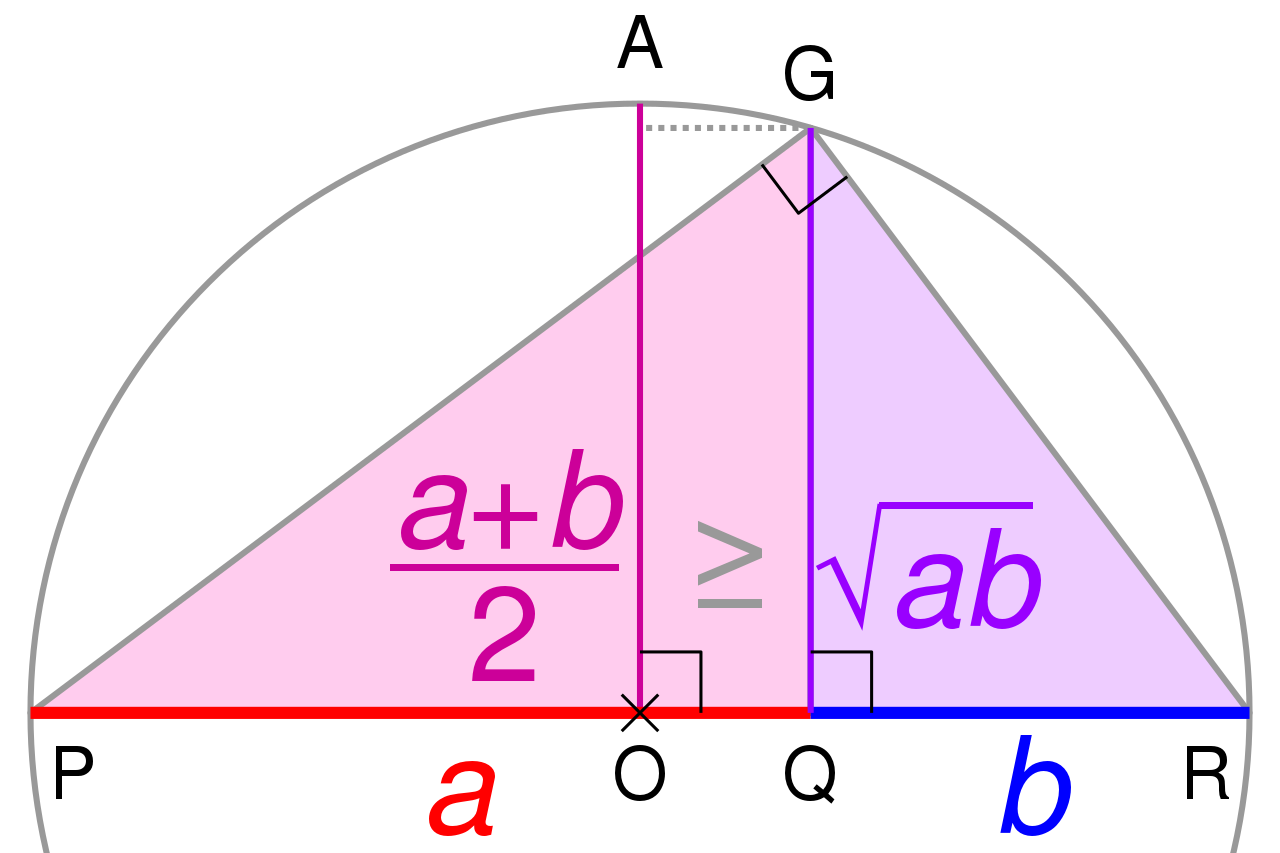
The following "proof without words" tells us two important facts for any positive real values $a$ and $b$:
the arithmetic mean $\frac{a+b}{2}$ of $a$ and $b$ will be greater than or equal to the geometric mean $\sqrt{ab}$; and
the arithmetic mean $\frac{a+b}{2}$ is always less than or equal to the larger of $a$ and $b$.
Taken together, we have $$\sqrt{ab} \le \frac{a+b}{2} \le \textrm{maximum of $a$ and $b$}$$
Now suppose $a=x_1$ and $b=\frac{c}{x_1}$.
Then notice the geometric mean of $a$ and $b$ is given by $$\sqrt{ab} = \sqrt{x_1 \cdot \frac{c}{x_1}} = \sqrt{c}$$
while the arithmetic mean of $a$ and $b$ is $$\frac{a+b}{2} = \cfrac{\frac{c}{x_1} + x_1}{2}$$ As such, we have $$\sqrt{c} \le \frac{\frac{c}{x_1} + x_1}{2} \le \textrm{maximum of $\frac{c}{x_1}$ and $x_1$}$$
Notably, if we (purposefully) overestimate with our initial guess for $\sqrt{c}$, then the following is a better estimation of $\sqrt{c}$ $$x_2 = \frac{\frac{c}{x_1} + x_1}{2}$$ As $x_2$ is still an overestimate of $\sqrt{c}$, we can repeat the process to find $$x_3 = \frac{\frac{c}{x_2} + x_2}{2}$$ which will thus be an even better overestimating approximation of $\sqrt{c}$
We can keep finding better and better estimates of $\sqrt{c}$ by finding $x_4$, $x_5$, $x_6$, etc., in the same exact way!
Interestingly, even if we started with an underestimate for $x_1$, the value $x_2$ that we find (i.e., the arithmetic mean) will still overestimate $\sqrt{c}$ (the geometric mean). Consequently, from that point forward $x_3$, $x_4$, $x_5$, etc., continue to be better and better estimates of $\sqrt{c}$ again.
Thus, any initial guess gives us the means to calculate $\sqrt{c}$ to whatever level of precision we might desire:
To find $\sqrt{c}$ for some positive real value $c$, make a guess $x_1$. Then find $x_2, x_3, x_4, \ldots$ with $$x_{i+1} = \cfrac{\frac{c}{x_i} + x_i}{2}$$
While a full discussion of how we measure the "speed of convergence" would take us beyond this course, it is worth noting that if our initial guess $x_1$ is even roughly "in the ballpark" of $\sqrt{c}$, this sequence of values $x_2, x_3, x_4, \ldots$ will very quickly converge on the square root of $c$!
Let's see how long it takes to calculate $\sqrt{2}$ to 8 decimal places with this method, using an initial guess of $1.5$: $$\begin{array}{rcl} x_1 &=& 1.5\\\\ x_2 &=& \cfrac{\frac{2}{1.5} + 1.5}{2} \approx 1.41666666\\\\ x_3 &=& \cfrac{\frac{2}{1.41666666} + 1.41666666}{2} \approx 1.41421569\\\\ x_4 &\approx& \cfrac{\frac{2}{1.41421569} + 1.41421569}{2} \approx 1.41421356\\\\ x_5 &\approx& \cfrac{\frac{15129}{1.41421356} + 1.41421356}{2} \approx 1.41421356\\\\ \end{array}$$
It didn't take long, did it! 😉