| | |
We have already seen how one can solve many equations that only involve a single variable for the value(s) of that variable that make the equation true. A natural question to then ask is what happens when an equation involves more than one variable?
For example, consider the simple equation $x^2 + y^2 = 25$. If we attempt to solve this equation for one variable, notice that for all $x \in (-5,5)$ there are two solutions for $y$. Likewise, for all $y \in (-5,5)$ there are two solutions for $x$. We can clearly say that neither $x$ or $y$ is a (single) function of the other. $$y = \pm \sqrt{25-x^2} \quad \textrm{ and } \quad x = \pm \sqrt{25-x^2}$$ That said, the $x$ and $y$ values that solve the equation discussed above are certainly related in some way. As such, we change our verbiage a bit. For any equation of two or more variables, the solution to that equation (i.e., the pairs of values that satisfy it) is called a relation.
One should note that just as we don't require an equation to describe a function (recall the peculiar way we described functions with arrows from one finite set to another, when we first introduced the notion of what a function was), we don't require an equation to describe a relation either. All we really need is a set of coordinate pairs (or $n$-tuples, more generally). Indeed, this is how a binary relation† is typically defined: a set of ordered pairs, where we say $x$ and $y$ are related only if $(x,y)$ is in the aforementioned set.
† : In case you are curious, a set of $n$-tuples -- that is, coordinates in $\mathbb{R}^n$ (possibly representing solutions to an equation with $n$ variables, but not required to do so) can be used to define a more general $n$-ary relation.
Of course, defining such relations through the identification of a set of ordered pairs naturally leads to graphs of relations -- i.e., plots of the coordinate pairs that make up the relation on a coordinate plane.
In the case above, note that $x^2 + y^2 = 25$ precisely when $\sqrt{x^2 + y^2} = 5$. By the Pythagorean Theorem the left side of that second equation represents the distance between a point $(x,y)$ and the origin $(0,0)$. Thus, we see the graph of the relation $\{(x,y) \in \mathbb{R}^2 \ | \ x^2 + y^2 = 25\}$ is a circle of radius $5$, centered at the origin.
As an important aside, note that more generally -- but for similar reasons -- we can say: $$\textrm{The graph of }\{(x,y) \in \mathbb{R}^2 \ | \ (x-h)^2 + (y-k)^2 = r^2\} \textrm{ is a circle with center $(h,k)$ and radius $r$}$$
Graphing $x^2 + y^2 = 25$ on the left below, note that it does not pass the vertical line test, which is consistent with our earlier observation that there is more than one $y$-value associated with several individual $x$-values (and vice-versa). As such, this relation can't be described by a single function.
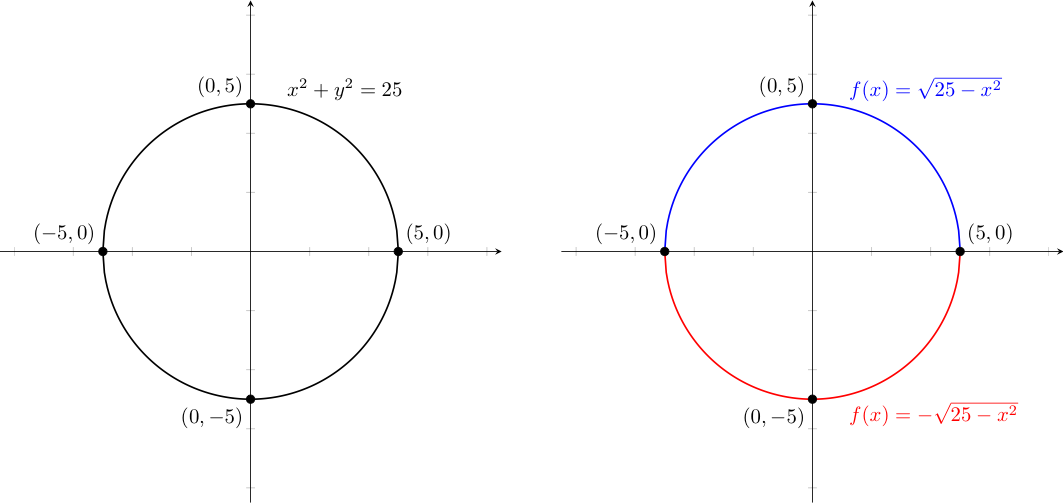
However, we can express this relation as the union of two function "pieces" (which we call branch functions) -- shown here by considering those points with negative vs. non-negative $y$-values in the red and blue semi-circles above, respectively. Nicely, we can consider the points $(-5,0)$ and $(5,0)$ to be part of one or both branch functions without any ill effects.
Importantly, while in this case it is easy to describe the blue and red functions using the formulas found when solving for $y$, it should be noted that not all equations in two variables $x$ and $y$ can be easily solved for $y$. A beautiful (and useful) example of this is discussed in the next section.
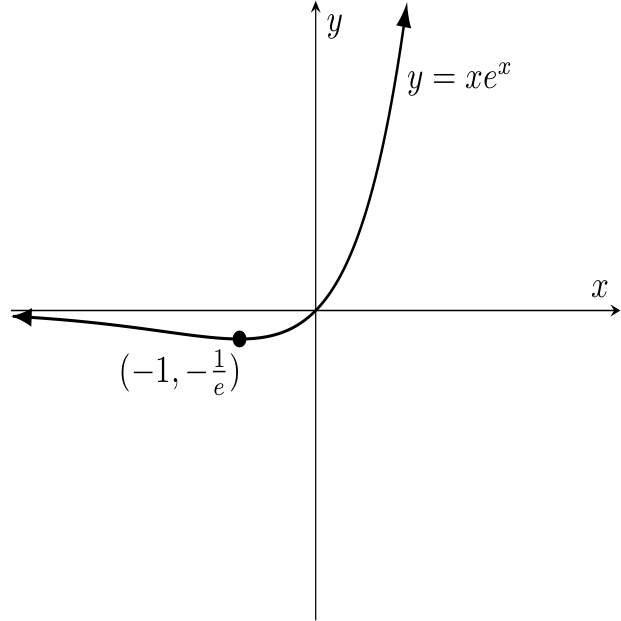
Focusing on the far left side of the graph, where $x$ is large in magnitude but negative, notice that $xe^x$ can be made arbitrarily small but stays negative. Consider $$-10 e^{-10} = -\frac{10}{e^{10}}, \quad -100 e^{-100} = -\frac{100}{e^{100}} \doteq , \quad -1000 e^{-1000} = -\frac{1000}{e^{1000}}$$ The denominators are growing much faster in magnitude than the numerators, although overall the fraction remains negative. As such, the graph of $y=xe^x$ should approach (from below) a horizontal asymptote formed by the $x$-axis.
At $x=-1$, note that $y = -\frac{1}{e}$ and at $x=0$, $y = 0 \cdot e^0 = 0 \cdot 1 = 0$.
Once $x$ is positive and increases without bound, $e^x$ certainly also increases without bound, as must then their product $xe^x$.
With all the above, we might come to the conclusion that the graph of $y=xe^x$ looks like the following:
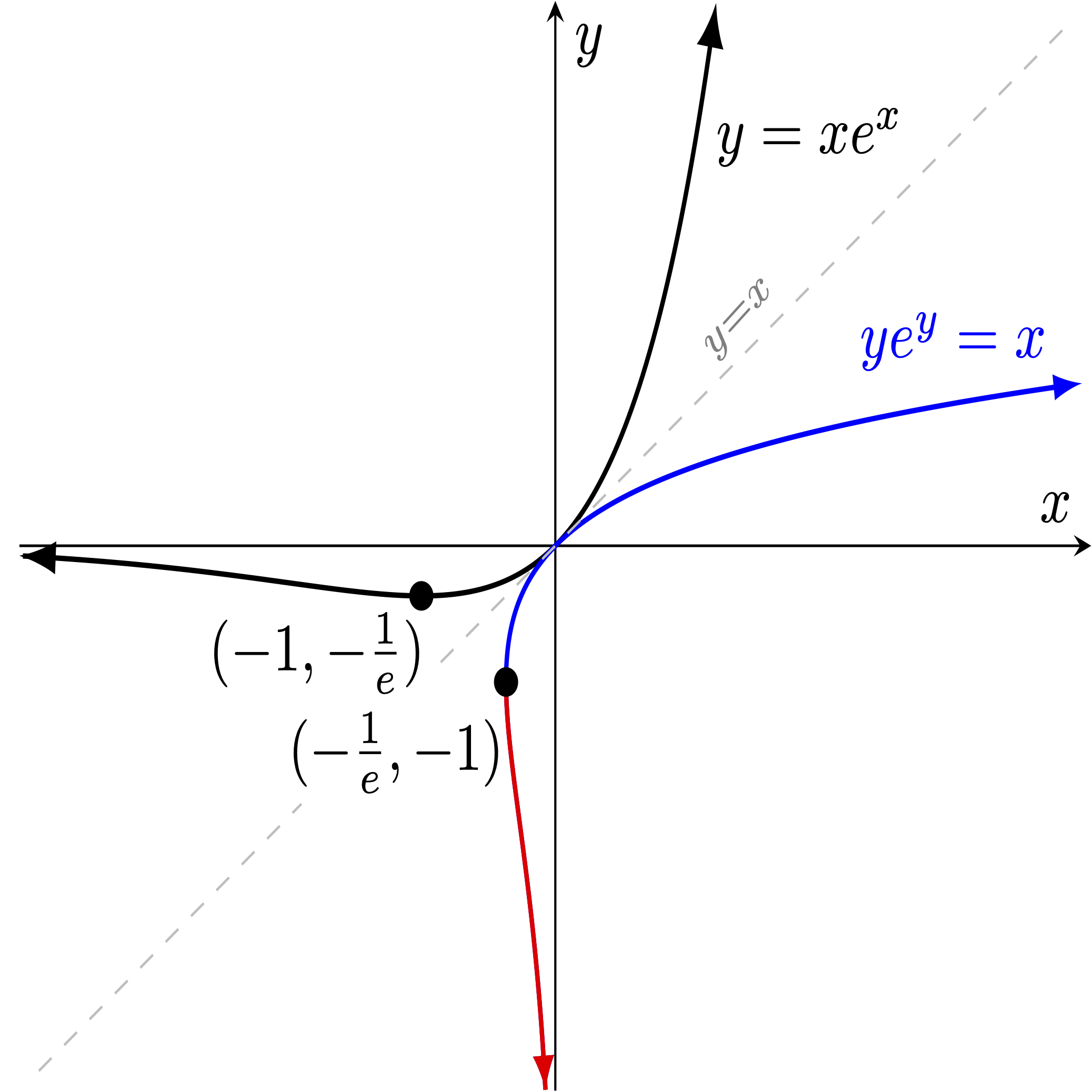
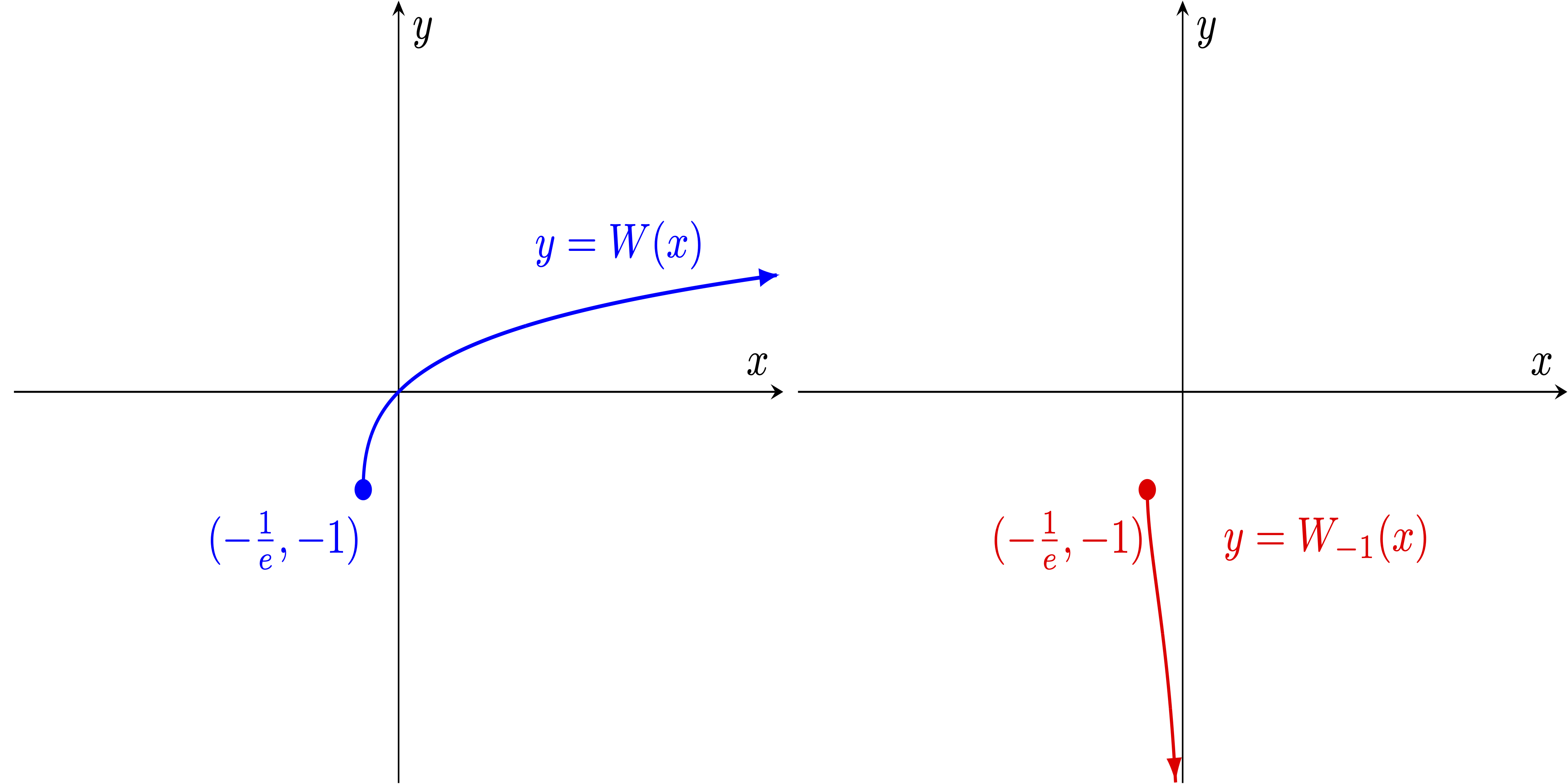
Of course, we can see by virtue of the blue curve not passing the vertical line test that the relation $ye^y = x$ can't be described by a single function, but we can still express this relation as the union of two branch functions. In this case, the two branch functions are determined by the section of the blue curve above and below height $-1$. Since finding an explicit formula for each branch is difficult‡, let us simply give them names. We call these two functions $W_0(x)$ (or simply $W(x)$ when the context is clear) and $W_{-1}(x)$, respectively.
‡ : Actually, finding an explicit formula for $W(x)$ is provably impossible if restricted to using only the functions we currently have introduced (or even the trigonometric ones to come)!
$W(x)$ is also known as Lambert's W function, so named by mathematicians Robert Corless and David Jeffrey of the University of Western Ontario in a paper they wrote along with Gaston Gonnet, David Hare, and Donald Knuth in 1996, as it has an interesting connection to solving equations of the form $x = q + x^m$, which was first accomplished by Johann Heinrich Lambert in 1758.
Some have suggested that the use of the letter $W$ is to honor British mathematician Sir Edward Wright, who did much of the initial exploration of this function, although others have argued its origin had more to do with a programming quirk in the mathematical software known as Maple.
Speaking of mathematical software, this function is not typically found on scientific calculators -- but $W_0(x)$ can be evaluated using the command productlog(x) in either Mathematica or wolframalpha.com. Similarly, $W_{-1}(x)$ can be found with productlog(-1,x) on both of these platforms.
Fascinatingly, $W(x)$ can be used to help us solve equations that otherwise would be unsolvable in terms of the functions we have explored so far! For the curious, examples follow.
In all of the problems below, our strategy is to note that $W(x)$ has inverse $W^{-1}(x) = xe^x$ and thus we seek or manufacture an occurrence of $xe^x$, or more generally $ue^u$ for some expression $u$ in terms of $x$. Then, we will re-interpret this as the inverse of Lambert's $W$ function and see where we can go from there -- often applying the socks and shoes strategy at that point:
|
Question Solution
|
|
Question Solution $$\begin{array}{rcll} (x^3 e^x)^{1/3} &=& 7^{1/3} & \quad {\Tiny \textrm{wanting to see $x$ instead of $x^3$ above, we cube root both sides}}\\ xe^{x/3} &=& 7^{1/3} & \quad {\Tiny \textrm{we can address the $x/3$ that popped up with a "u-substitution" of $u = x/3$ (so $x=3u$)}}\\ 3u e^u &=& 7^{1/3} & \quad {\Tiny \textrm{letting us now take advantage of the inverse of Lambert's $W$ function}}\\ 3W^{-1}(u) &=& 7^{1/3} & \quad {\Tiny \textrm{from here, its socks and shoes!}}\\ W^{-1}(u) &=& \frac{1}{3} \cdot 7^{1/3} & \\ u &=& W(\frac{1}{3} \cdot 7^{1/3})\\ \end{array}$$ Just don't forget that we actually want a solution for $x$, not $u$. So recalling that $x=3u$, we have $$\textstyle{x = 3 W(\frac{1}{3} \cdot 7^{1/3})}$$ |
|
Question Solution $$\begin{array}{rcll} x^x &=& 4 & \quad {\Tiny \textrm{address the lack of $e$ by taking the natural log of both sides}}\\ \ln x^x &=& \ln 4 & \quad {\Tiny \textrm{properties of logs lets us pull the exponent $x$ to the front of the left side}}\\ x \ln x &=& \ln 4 & \quad {\Tiny \textrm{using the fact that $e^x$ and $\ln x$ are inverses, we can introduce a $e^u$ factor}}\\ e^{\ln x} \cdot \ln x &=& \ln 4 & \quad {\Tiny \textrm{nicely, simply commuting the factors on the left reveals the desired $ue^u$ form!}}\\ (\ln x) \cdot e^{\ln x} &=& \ln 4 & \quad {\Tiny \textrm{now use the inverse of Lambert's $W$ function}}\\ W^{-1}(\ln x) &=& \ln 4 & \quad {\Tiny \textrm{from here, it's socks and shoes..}}\\ \ln x &=& W(\ln 4) &\\ x &=& e^{W(\ln 4)} \end{array}$$ |
|
Question Solution
Recall that the graph of the relation $ye^y = x$ is built from two functions, $W(x)$ and $W_{-1}(x)$. The first had domain $[-\frac{1}{e},\infty)$, the second had domain $[-\frac{1}{e},0)$. Consequently, when we have $u(x) e^{u(x)} = c$ where $c$ is in $[-\frac{1}{e},0)$, there are actually two possible conclusions: either $$W_{0}^{-1}(u(x)) = c \quad \textit{or} \quad W_{-1}^{-1}(u(x)) = c$$ As such, $$\textstyle{W_0^{-1}(-2x) = -\frac{1}{3} \quad \textit{or} \quad W_{-1}^{-1}(-2x) = -\frac{1}{3}}$$ Then proceeding with a socks and shoes strategy on both possibilities: $$\begin{array}{rcl} -2x &=& W_0 \left(-\frac{1}{3} \right) \quad \textit{or} \quad W_{-1} \left(-\frac{1}{3} \right)\\ x &=& -\frac{1}{2}W_0 \left(-\frac{1}{3} \right) \quad \textit{or} \quad -\frac{1}{2}W_{-1} \left(-\frac{1}{3} \right) \end{array}$$ |
|
Question Solution $$\begin{array}{rcll} x^5 &=& 8^x & \quad {\Tiny \textrm{address both the extra exponent $5$ and lack of $e$, by taking a natural log of both sides}}\\ \ln x^5 &=& \ln 8^x & \quad {\Tiny \textrm{properties of logs lets us pull the exponents to the front of each expression}}\\ 5\ln x &=& x \ln 8 & \quad {\Tiny \textrm{divide both sides by $5x$ to get variables on one side, constants on the other}}\\ (\ln x) \cdot (\frac{1}{x}) &=& \frac{\ln 8}{5} & \quad {\Tiny \textrm{we can introduce an $e^u$ using the inverse properties of $e^x$ and $\ln x$}}\\ (\ln x) \cdot e^{\ln \frac{1}{x}} &=& \frac{\ln 8}{5} & \quad {\Tiny \textrm{we almost have $ue^u$ form on the left -- rewrite $1/x$ as a power to get closer}}\\ (\ln x) \cdot e^{\ln x^{-1}} &=& \frac{\ln 8}{5} & \quad {\Tiny \textrm{then use log properties to pull the negative exponent out of the log}}\\ (\ln x) \cdot e^{-\ln x} &=& \frac{\ln 8}{5} & \quad {\Tiny \textrm{not essential -- but we can write the right side more compactly using log properties}}\\ (\ln x) \cdot e^{-\ln x} &=& \ln \sqrt[5]{8} & \quad {\Tiny \textrm{now, the first factor is just missing a negative -- so negate both sides}}\\ (-\ln x) \cdot e^{-\ln x} &=& -\ln \sqrt[5]{8} & \quad {\Tiny \textrm{success! now we can use the inverse of Lambert's $W$ function}}\\ \end{array}$$ However, as the value on the right side is in $[-\frac{1}{e},0)$ we must again consider two cases: $$W_0((-\ln) \cdot e^{-\ln x}) = -\ln \sqrt[5]{8} \quad \textit{or} \quad W_{-1}((-\ln) \cdot e^{-\ln x}) = -\ln \sqrt[5]{8}$$ Now we proceed with the socks and shoes strategy: $$\begin{array}{rcl} -\ln x &=& W_0(-\ln \sqrt[5]{8}) \quad \textit{or} \quad W_{-1}(-\ln \sqrt[5]{8})\\ \ln x &=& -W_0(-\ln \sqrt[5]{8}) \quad \textit{or} \quad -W_{-1}(-\ln \sqrt[5]{8})\\ x &=& e^{-W_0(-\ln \sqrt[5]{8})} \quad \textit{or} \quad e^{-W_{-1}(-\ln \sqrt[5]{8})}\\ \end{array}$$ |