

 |  |
What is the implicit domain (in set-builder notation) of $\displaystyle{f(x) = \frac{(x-7)^2\log_2(x+5)}{x-7}}$
The domain of the $\log_2 x$ is $\mathbb{R}_{>0}$, so we need $x \gt -5$. Further, we need $x \neq 7$ so that we don't divide by zero. Thus, the implicit domain of the $f$ above is $\{x \in \mathbb{R} \ | \ x \gt -5 \textrm{ and } x \neq 7\}$.
Does the graph below represent a function? Explain how you know.
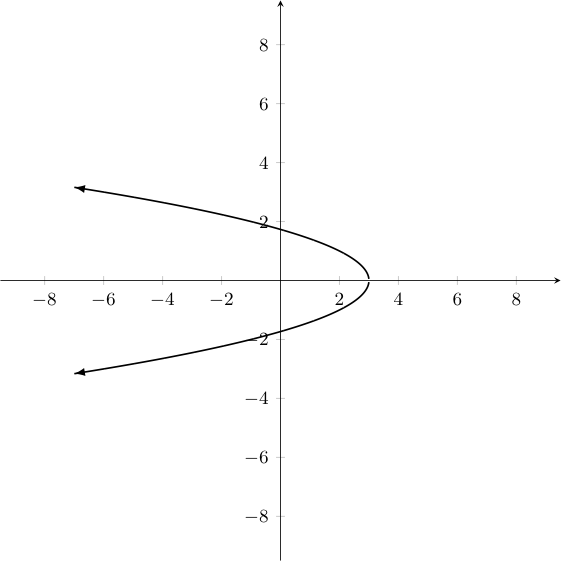
No, it does not pass the vertical line test.
Given the graph of the function $f(x)$ below:
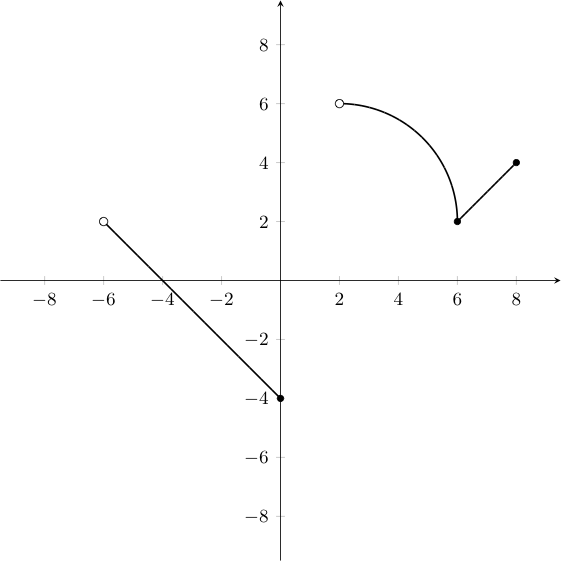
Find the following sum, expressing your answer in base $5$, doing so without converting to another base first. $$(4213)_5 + (2334)_5$$
Express the following combination of polynomials (of two variables) as a single polynomial of two variables: $$(3a - 2b)(5a + ab - 4b) + (22ab + 2ab^2)$$
$\displaystyle{15a^2 + 8b^2 + 3a^2b}$
Factor completely: $x^5 - 9x^3 -8x^2 + 72$
Use factoring by grouping first, and then use difference of squares and difference of cubes factor what results to obtain: $$(x-3)(x+3)(x-2)(x^2+2x+4)$$
Decide if Eisenstein's Criterion can be used to prove the following polynomial is irreducible. If it can, find the prime $p$ in question. If not, explain why not. $$x^5 + 9x^4 - 15x^3 + 3x^2 + 21$$
Eisenstein's Criterion apples with $p=3$ (note: $p$ does not divide the coefficient on $x^5$, but divides all other coefficients (i.e., $9$, $-15$, $3$, and $21$), and $p^2$ does not divide the constant term, $21$). The polynomial given is irreducible -- it does not factor into a product of polynomials with integer coefficients.
Divide $f(x)$ by $g(x)$, expressing your answer in quotient-remainder form: $$f(x) = x^4 - 3x^3 + 2x^2 - 5 \quad \quad g(x) = x^2 - 2x + 1$$
$\displaystyle{x^4 - 3x^3 + 2x^2 - 5 = (x^2 - 2x + 1)(x^2 -x -1) + (-x-4)}$
Find both the additive and the multiplicative inverses of $4$ in a $13$-hour clock arithmetic.
$9$ is the additive inverse; $10$ is the multiplicative inverse
The set $S = \{A,B,C,D\}$, along with addition and multiplication as described by the tables below is a commutative ring. Explain why it is not also a field. $$\begin{array}{c|cccc} + & A & B & C & D\\\hline A & A & B & C & D\\ B & B & C & D & C\\ C & C & D & C & B\\ D & D & C & B & A \end{array} \quad \quad \begin{array}{c|cccc} \times & A & B & C & D\\\hline A & A & A & A & A\\ B & A & B & C & D\\ C & A & C & A & C\\ D & A & D & C & B \end{array}$$
Note that $A$ plays the role of zero (i.e., the additive identity), as $A+x = x+A = x$ for any $x \in S$. Further, $B$ plays the role of one (i.e., the multiplicative identity), as $Bx = xB = x$ for the same. However, this makes $C$ a non-zero element who does not have a multiplicative inverse.
Simplify each expression below, assuming it is defined. You may leave your answer in factored form.
$\displaystyle{\frac{x^2 + 6x + 9}{4x+12} \div \frac{2x^2+5x-3}{6x}}$
$\displaystyle{\frac{x-2}{x^3 + 6x^2 + 5x} - \frac{1}{x^2 + 3x + 2}}$
$\displaystyle{\frac{3x}{2(2x-1)}}$
$\displaystyle{\frac{-(5x+4)}{x(x+1)(x+2)(x+5)}}$
Find the simplified difference quotient $\cfrac{f(x+h)-f(x)}{h}$ for $f(x) = x^3$, assuming $h \neq 0$
$\displaystyle{3x^2 + 3xh + h^2}$
Recalling $\mathbb{Q}(\sqrt{5})$ is a field, find rational values $c$ and $d$ so that $$\frac{1}{7 + 3\sqrt{5}} = c + d\sqrt{5}$$
$c = \frac{7}{4}$ and $d = -\frac{3}{4}$
Express in interval notation where the graph of $f(x) = x^3 + 2x^2$ is above the graph of $g(x) = 25x+50$.
$\displaystyle{(-5,-2) \cup (5,\infty)}$