

 |  |
Simplify and express the following in form $a+bi$ where $a$ and $b$ are real numbers.
$-\sqrt{81}$
$\sqrt{-28}$
$(-6-5i)+(9+2i)$
$(-11 + 4i)+(6+8i)$
$(8-3i)-(9-i)$
$(1-2i)(1+3i)$
$(5-2i)(-1+i)$
$(3+\sqrt{-16})(2+\sqrt{-25})$
$(7-\sqrt{-16})(2+\sqrt{-9})$
$(5-4i)(5+4i)$
$(3+2i)(3-2i)$
$(3+4i)(3-4i)$
$(8+i)(8-i)$
$(-2+7i)^2$
$(6+5i)^2$
$\displaystyle{\frac{i}{2+i}}$
$\displaystyle{\frac{5-i}{-7+2i}}$
$\displaystyle{\frac{1+i}{(1-i)^2}}$
$\displaystyle{\frac{4-2i}{1+i} + \frac{2-5i}{1+i}}$
$\displaystyle{\frac{3+2i}{1-i} + \frac{6+2i}{1-i}}$
$0 + 9i$
$0 + 4i\sqrt{7}$
$3-3i$
$-5+12i$
$-1-2i$
$7+i$
$-3+7i$
$-14+23i$
$26+13i$
$41$
$13$
$25$
$65$
$-45-28i$
$11+60i$
$\frac{1}{5} + \frac{2}{5}i$
$\frac{-37}{53} - \frac{3}{53}i$
$\frac{1}{2} + \frac{1}{2}i$
$-\frac{1}{2} - \frac{13}{2}i$
$\frac{5}{2} + \frac{13}{2}i$
Evaluate/simplify
$i^{11}$
$i^{24}$
$(-i)^{71}$
$(2i)^5$
$(5i)^4$
$|3 + 4i|$
$|5 + 12i|$
$\left|\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}i\right|$
$\left|\frac{1}{2} - \frac{\sqrt{3}}{2}i\right|$
$|-i|$
$\arg(-i)$ in $[0,360^{\circ})$
$\arg(-1)$ in $[0,360^{\circ})$
$\arg(-3+3i)$ in $[0,360^{\circ})$
$\arg(i)$ in $[0,360^{\circ})$
$-i$
$1$
$i$
$32i$
$625$
$5$
$13$
$1$
$1$
$1$
$270^{\circ}$
$180^{\circ}$
$135^{\circ}$
$90^{\circ}$
Use the given information to determine the value of the last expression for each.
$\arg(z_1) = 45^{\circ}, \arg(z_2) = 30^{\circ}; \arg(z_1 \cdot z_2) = \, ?$
$\arg(z_1) = -180^{\circ}, \arg(z_2) = 60^{\circ}; \arg(z_1 \cdot z_2) = \, ?$
$\arg(z_1) = \frac{180}{7}, \arg(z_2) = \frac{180}{3}; \arg(z_1 \cdot z_2) = \, ?$
$\arg(z_1) = 60^{\circ}, \arg(z_2) = 30^{\circ}; \arg\left(\displaystyle{\frac{z_1}{z_2}}\right) = \, ?$
$75^{\circ}$
$-120^{\circ}$
$\frac{600}{7}$
$30^{\circ}$
Show that the unit circle in the complex plane is the set of all $z \in \mathbb{C}$ where $z = 1\, /\,\overline{z}$.
Note that if $z = 1\, /\,\overline{z}$, then $z \cdot \overline{z} = 1$. Then recall (or show) that $z \cdot \overline{z} = |z|$. As such, $|z| = 1$, which is the defining property for being on the unit circle.
Complete the following beautiful proof of Heron's formula (created by high schooler, Miles Dillon Edwards) which says:
The area of a triangle $\mathscr{A}$ with sides $a$, $b$, and $c$, and semi-perimeter $\displaystyle{ s = \frac{a+b+c}{2}}$ is given by $$\mathscr{A} = \sqrt{s(s-a)(s-b)(s-c)}$$
Proof:
Consider the following image. Let the point marked $I$ be the center of the incenter of $\triangle ABC$‡, with the radius of the related inscribed circle being $r$. Let $a=y+z$, $b=x+z$, and $c=x+y$ be the lengths of the sides opposite $A$, $B$, and $C$, respectively. Consequently, the semi-perimeter $s = x + y + z$.
Note that the triangles that appear congruent below must actually be so since corresponding side lengths agree. Thus, we must also have corresponding pairs of angles in these congruent triangles also congruent (as marked $\alpha$, $\beta$, and $\gamma$).
Considering a full rotation around $I$, it must then be the case that $2\alpha + 2\beta + 2\gamma = 360^{\circ}$, so $\alpha + \beta + \gamma = 180^{\circ}$.
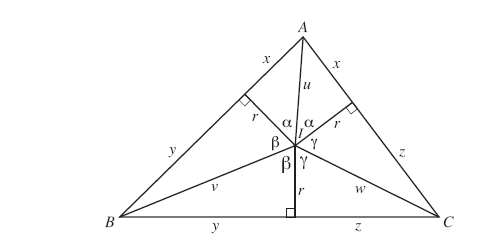
Now imagine moving the triangle with marked angle $\alpha$ and one side on $\overline{AC}$ so that $I$ ends up at the origin, the segment of length $r$ on the $x$-axis, and the segment of length $x$ on the $y$-axis. As a result, $A$ ends up at the complex value $z_A = (r+ix)$.
Moving two other triangles similarly (with both moving $I$ to the origin, and the segment of length $r$ to the $x$-axis), get $B$ to move to $z_B = r+iy$ and $C$ to move to $z_C = r+zi$.
Recalling that $\textrm{cis}(\theta)$ returns the complex value resulting from rotating $1$ counter-clockwise through an angle of $\theta$ about the origin (i.e., zero), observe that $$\begin{array}{rcl} z_A z_B z_C &=& (r+ix)(r+iy)(r+iz)\\ &=& (|z_A| \cdot \textrm{cis}(\arg(z_A)) \cdot (|z_B| \cdot \textrm{cis}(\arg(z_B)) \cdot (|z_C| \cdot \textrm{cis}(\arg(z_C))\\ &=& |z_A| \cdot |z_B| \cdot |z_C| \cdot \textrm{cis}(\arg(z_A)) \cdot \textrm{cis}(\arg(z_B)) \cdot \textrm{cis}(\arg(z_C))\\ &=& |z_A| \cdot |z_B| \cdot |z_C| \cdot \textrm{cis}(\arg(z_A) + \arg(z_B) + \arg(z_C))\\ &=& |z_A| \cdot |z_B| \cdot |z_C| \cdot \textrm{cis}(180^{\circ})\\ &=& |z_A| \cdot |z_B| \cdot |z_C| \cdot (-1) \end{array}$$
Noting the last expression above is real, the imaginary coefficient of $(r+ix)(r+iy)(r+iz)$ must be zero.
Find this imaginary coefficient in terms of $x$, $y$, $z$, and $r$, and using the fact that it must be $0$, solve for $r$ in terms of $x$, $y$, and $z$ to deduce Heron's formula from there.
‡ : The incenter of a triangle is the single point where the lines that bisect the three angles of a triangle all meet. The fact that the three angle bisectors all intersect at a single point may be surprising. However, consider placing a small circle inside the triangle. Now inflate that circle, allowing it to move about on the inside of the triangle. There is a moment when the circle can't expand any further without leaving the confines of the triangle. This circle will be tangent to all 3 sides of the triangle (if not, there is room to expand), and thus considering any two such sides has center on the related angle bisector. As such the center of this inscribed circle is the incenter.
Note that $$0 = Im((r+ix)(r+iy)(r+iz)) = r^2(x+y+z) - xyz$$ so $$r = \sqrt{\frac{xyz}{x+y+z}} = \sqrt{\frac{(s-a)(s-b)(s-c)}{s}}$$ We then have the area of $\triangle ABC$ is $$\begin{array}{rcl} Area(\triangle BCI) + Area(\triangle ACI) + Area(\triangle ABI) &=& \frac{ra}{2} + \frac{rb}{2} + \frac{rc}{2}\\ &=& r \left(\frac{a+b+c}{2}\right)\\ &=& r \cdot s\\ &=& \sqrt{s(s-a)(s-b)(s-c)} \end{array}$$
Draw an arbitrary quadrilateral and erect squares on all four sides (on the outside of the quadrilateral). Then find the centers of these squares. Show the segments connecting the centers of each pair of squares opposite one another are perpendicular and of equal length.

Denote the vertices of the quadrilateral as $z_a$, $z_b$, $z_c$, and $z_d$. Then, find the complex numbers that match the other points drawn (in particular the centers of the squares). Remember that multiplication by $i$ rotates a complex value $90^{\circ}$ about the $0$ (the origin). Show the difference between the endpoints of one of these segments is $i$ times the difference between the endpoints of the other.