

 |  |
There are other ways to combine functions to create new ones. Recall when we earlier introduced the absolute value function, we made mention that it was "piecewise defined". Here we explore functions of this type a bit further.
To create a "piece-wise defined" function, one breaks apart some domain into two or more disjoint pieces, using different functions to calculate the output for each $x$-value, where the function used is based upon the piece into which that particular $x$-value falls.
Again considering the absolute value function, $|x|$, recall that when $x \ge 0$, the absolute value function doesn't really do anything -- it returns its input unchanged. So, for this "piece" $|x| = x$.
However, when $x \lt 0$, the absolute value changes the sign of its input. Multiplying a value by negative one has the same effect -- so we can say that for this second "piece" $|x| = -x$.
Thus, we summarize how to calculate the output by cases, depending on which "piece" applies: $$|x| = \left\{ \begin{array}{ccc} x & , & x \ge 0\\ -x & , & x \lt 0 \end{array} \right. $$
Graphing a piecewise function can be accomplished by simply graphing the functions found in the respective "pieces", limiting the points drawn for each piece to the $x$-values that satisfy the appropriate condition.
For example, given the function $$f(x) = \left\{ \begin{array}{ccc} \sqrt{25-x^2} & , & x \le 3\\ 2x-5 & , & x \gt 3 \end{array} \right. $$
We find its graph by first graphing $y = \sqrt{25-x^2}$. As we have in the past, we can do this relatively easily upon realizing we can write this piece as a compositional chain of simpler functions: $$x^2 \longrightarrow (-x) \longrightarrow (x+25) \longrightarrow \sqrt{x}$$
Following the most direct process for graphing such compositions, we start by graphing the first (inner-most) function applied to $x$. In this case, that will result in a parabola opening upwards with its point of minimum height (i.e., the vertex) at $(0,0)$.1 Then, we reflect the graph over the $x$-axis to accomplish the reflection.2 We translate/shift the result (vertically) upwards by $25$ units to account for the addition of $25$ -- and solve $25-x^2 = 0$ to discover $x$-intercepts at $(\pm 5,0)$.3 Lastly, we just need to apply the transformation corresponding to the square root function.
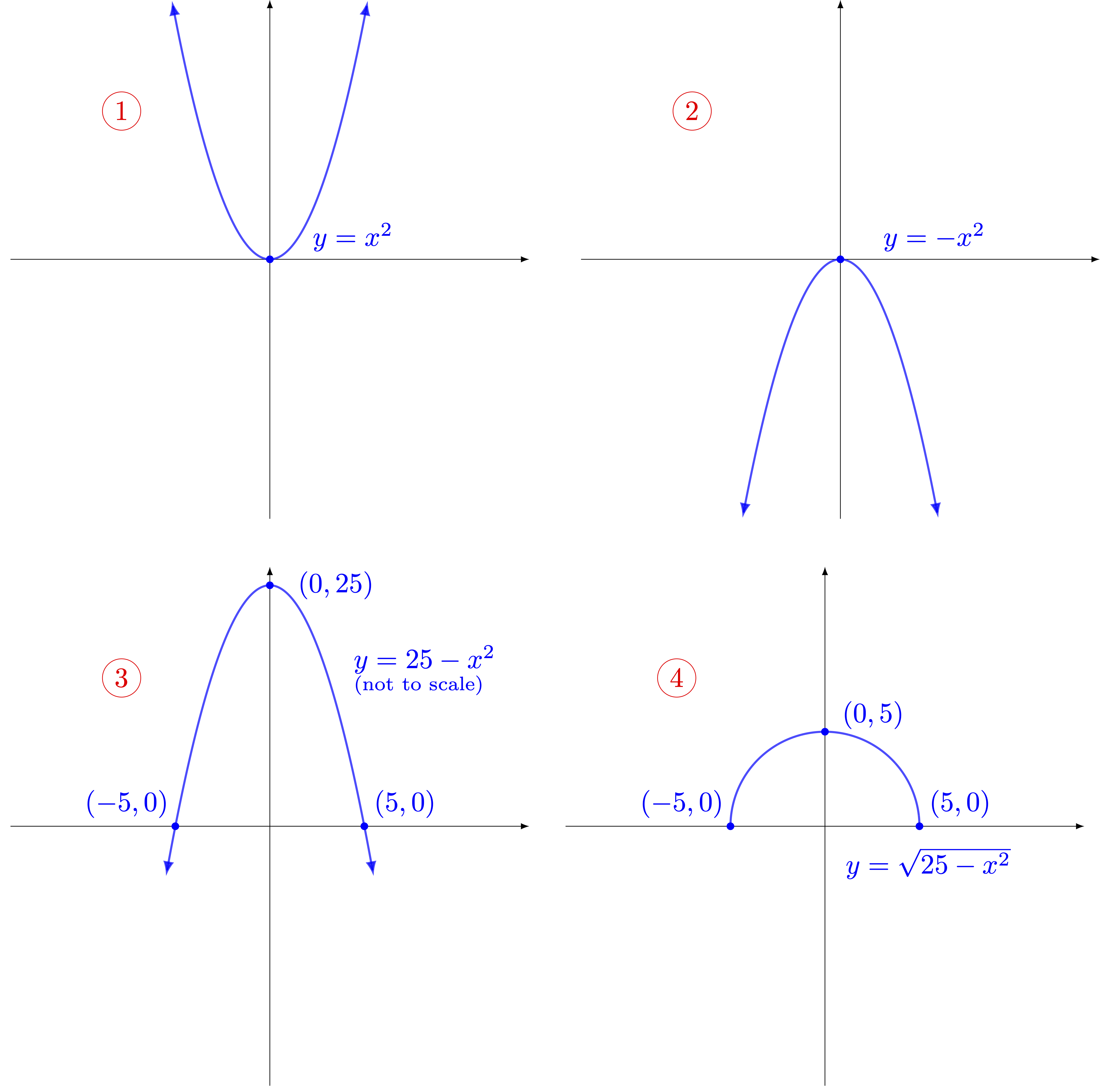
Applying this last transformation requires we recognize a few things. Certainly the vertex which had moved to $(0,25)$ will now be at $(0,5)$ given that $\sqrt{25} = 5$. Also, the $x$-intercepts previously at $(\pm 5,0)$ will stay where they are as $\sqrt{0} = 0$. Importantly however, wherever the graph had been below the $x$-axis -- namely, anywhere in $(-\infty,-5) \cup (5,\infty)$ -- we end up taking the square root of a negative which we know can not be a real value. As such, the points of the graph disappear for any $x$ values where this happens.
Upon sketching the final graph associated with $y = \sqrt{25-x^2}$, it appears the result is a semi-circle4 which has center at the origin and radius $5$. In fact, it is exactly that -- which we will prove in the next section!
Turning our attention to the easier $y=2x-5$ piece, we can graph the related function by simply starting with the identity function,1 vertically scaling it by a factor of two2 and translating it (vertically) down $5$ units3. Note, these transformations will preserve the linear nature of the original identity function, so the final graph stays "straight". Further, we can find $2(0)-5$ to locate its $y$-intercept at $(0,-5)$ and solve $2x-5=0$ to discover its $x$-intercept at $(5/2,0)$.
As our final (and most important) step to graph our piecewise function $f(x)$, we plot both graphs obtained above on the same axes, but discard those points whose $x$-coordinates don't match the conditions provided for the first, semi-circular piece (i.e., the dashed part shown in a cyan below) and similar points whose $x$-coordinates don't match the conditions provided for the second, linear piece (i.e., the dashed part shown in purple below). Upon removal of these points, we can finally see the graph of the piecewise function sought (at right below).
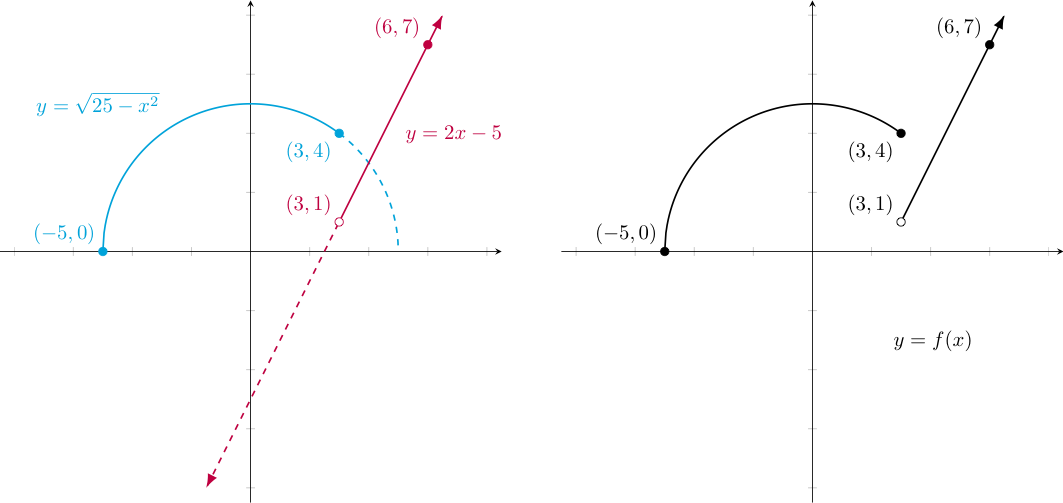
There is one detail to which we should pay special attention. Note that we use a filled-in point at $(3,4)$ to suggest that the output of the function at $x=3$ is determined by the semi-circular piece -- since the condition on this piece is true when $x=3$. Likewise, to indicate that the point where $x=3$ should be excluded from the linear piece (given the strict inequality), we place an open circle at $(3,1)$.
The domain of the piecewise-defined function is the set of all $x$ values that: 1) satisfy one of its various conditions, and 2) produce some (real-valued) output. So in the example above, the domain would be $[-5,\infty)$. The image/range, as always, is the set of all output values (i.e., heights) produced by the function. In the example above, the range would be given by $[0,\infty)$.