• About
• Statistics
• Number Theory
• Java
• Data Structures
• Cornerstones
• Calculus

The Arithmetic of Permutations (and Commutators)

One may have noticed that in a braid, the strands that start out at given positions don't always end up in those same positions. If we color the strands, this has the effect of changing the order of the colors seen on one end of the braid from what they were on the other.

As an example, in the braid below, from the left side to the right, the order of colors changes in the following way: $$\{\textrm{red, green, blue, orange, black}\} \longrightarrow \{\textrm{red, black, green, blue, orange} \}$$

Interestingly, focusing only on how the order of the colors has changed yields another strange arithmetic...

Let us call the act of changing the order of some sequence of $n$ elements a permutation of $n$ elements^†.

^† Note: one can also talk about permutations in the context of an infinite number of elements -- but to keep things simple for the moment, let us assume all the permutations discussed below involve only a finite number of elements $n$

The generic term "elements" used in the definition above is purposeful -- these might be colored strands in a braid, or people in a line, or paintings on a wall. We don't really care what the "elements" are -- only how their order is changing.

One natural notation we might adopt to identify a permutation is to create a matrix whose top row consists of the consecutive numbers from $1$ to $n$ in that order, representing the initial positions of the elements, and whose bottom row consists of the positions of the elements after the permutation has occurred.

As an example, we might represent the permutation of colors induced by the braid above with the following -- where each vertical pair corresponds to the positions where a single color started and ended. $$\begin{bmatrix} 1 & 2 & 3 & 4 & 5\\ 1 & 3 & 4 & 5 & 2 \end{bmatrix}$$

Note also that one can easily find a braid on $n$ strands that induces any given permutation on $n$ elements. (Indeed, there are many different braids for any single given permutation.)

As an example, consider the permutation given by $$\begin{bmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ 3 & 1 & 4 & 6 & 5 & 2 \end{bmatrix}$$ Simply write to columns of numbers $1,2,3,4,5,6$ and connect with straight lines of different colors the vertical pairs seen in the matrix above (see the image on the left, below). Remember, we don't care anymore about which strand crosses over which other strand -- so these can be chosen at random. The only thing one needs to worry about is more than two lines crossing at the same exact point. In such instances, one can always "jiggle" the strands involved left or right a bit to avoid that from happening. Then we can "clean up" the braid (see the image on the right, below) to more easily identify its braid word, if that is desired.

   

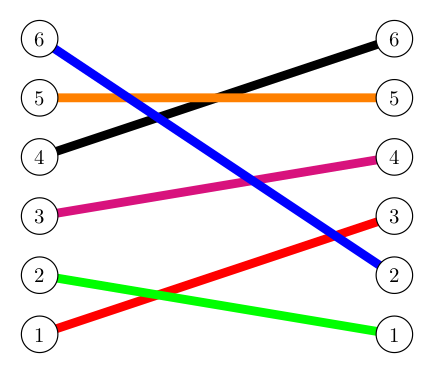
Given that we can always find a braid in this way that will induce any given permutation we encounter, permutations on $n$ elements will share many of the same properties enjoyed by braids on $n$ strands.

Recall that we could combine braids (with an equal number of strands) through concatenation to create a new braid. We did this by placing one braid after the other, and then fusing them together.

In a very connected way, we can combine any two permutations (on $n$ elements) to produce a third permutation (also on $n$ elements) by applying one permutation after the other. The resulting permutation is called the composition of the other two.

As it seems timely to mention it -- notice this means this operation of "composing permutations" is closed.

We must be careful though -- depending on which permutation we apply first, we run the risk of getting different permutations. So to be concrete: if $P_1$ and $P_2$ represent two permutations of $n$ elements, let us define their composition (product?), denoted by $P_1 * P_2$, to be the permutation produced by applying $P_1$ first and then $P_2$ to the result.^‡

^‡Note: we choose this order so that we can draw upon what we know about braids -- but be aware in some textbooks and other resources the reader might find online, such compositions are evaluated from right to left instead.

As an example, $$\begin{bmatrix} 1 & 2 & 3 & 4 & 5\\ 2 & 4 & 3 & 5 & 1 \end{bmatrix} * \begin{bmatrix} 1 & 2 & 3 & 4 & 5\\ 5 & 4 & 1 & 2 & 3 \end{bmatrix} = \begin{bmatrix} 1 & 2 & 3 & 4 & 5\\ 4 & 2 & 1 & 3 & 5 \end{bmatrix}$$

Here's the same product represented in a more braid-like form:

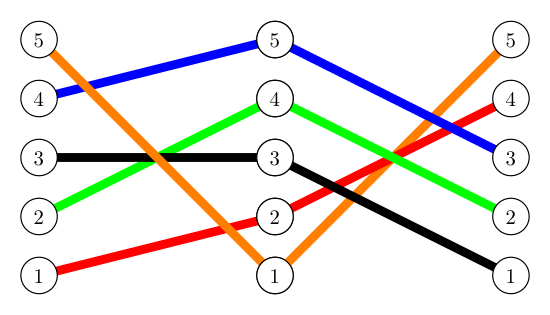
For example, notice that above [the element at position] $1$ moves to [position] $2$ in the first permutation. Also notice that $2$ similarly moves to $4$ in the second permutation. Thus, when both of these happen in the product/composition of the two permutations, we have $1$ moving to $4$. This gives us the first column of the product matrix.

Likewise (and reading each arrow shown as "moves to"), we see $2 \rightarrow 4$ in the first permutation, and $4 \rightarrow 2$ in the second. So $2 \rightarrow 2$ in their product, as indicated by the second column in the product matrix.

Continuing in this fashion: $3 \rightarrow 3$ in the first, $3 \rightarrow 1$ in the second, so $3 \rightarrow 1$ in their product; $4 \rightarrow 5$ in the first, $5 \rightarrow 3$ in the second, so $4 \rightarrow 3$ in their product; and finally $5 \rightarrow 1$ in the first, $1 \rightarrow 5$ in the second, so $5 \rightarrow 5$ in their product. These pairs give us the 3rd, 4th, and 5th columns of the product matrix, respectively.

Readers will want to ensure they see how to trace "what goes to what" to produce the product matrix directly from the two matrices being multiplied (without having to draw the braid-like picture).

As a matter of convenience (and as we have done before for both braids and the multiplication of variables representing real values), we often drop the "$*$" symbol (i.e., we write $P_1 P_2$ instead of $P_1 * P_2$).

Like their braided cousins, permutations are not generally commutative. As an example,

However, permutations on $n$ elements are associative. That is to say, for any such permutations $P_1, P_2, P_3$, we have $(P_1 P_2) P_3 = P_1 (P_2 P_3)$, as the following suggests: $$ \begin{array}{rcl} \left( \begin{bmatrix} 1 & 2 & 3 & 4\\ 2 & 4 & 3 & 1 \end{bmatrix} \begin{bmatrix} 1 & 2 & 3 & 4\\ 1 & 3 & 4 & 2 \end{bmatrix} \right) \begin{bmatrix} 1 & 2 & 3 & 4\\ 2 & 1 & 4 & 3 \end{bmatrix} & = & \begin{bmatrix} 1 & 2 & 3 & 4\\ 3 & 2 & 4 & 1 \end{bmatrix} \begin{bmatrix} 1 & 2 & 3 & 4\\ 2 & 1 & 4 & 3 \end{bmatrix}\\\\ & = & \begin{bmatrix} 1 & 2 & 3 & 4\\ 4 & 1 & 3 & 2 \end{bmatrix} \end{array} $$

We can define a special identity permutation on $n$ elements that leaves the order of the corresponding $n$ elements unchanged, denote this permutation by $I$:

Not surprisingly given its name, this permutation functions in the anticipated way: For any permutation $P$, we have $P * I = I * P = P$. The reader should check this on a permutation $P$ of their choosing.

Inverses exist too, and are simply constructed by flipping the vertical pairs seen upside-down and re-ordering the columns to again see $1$ to $n$ in the top row: $$ \begin{bmatrix} 1 & 2 & 3 & 4\\ 4 & 1 & 3 & 2 \end{bmatrix}^{-1} = \begin{bmatrix} 1 & 2 & 3 & 4\\ 2 & 4 & 3 & 1 \end{bmatrix} $$

The reader might want to verify the product of the permutation and its inverse shown above is indeed the identity permutation. This should be checked in both directions, as $x$ and $x^{-1}$ are inverses if and only if $x \cdot x^{-1} = x^{-1} \cdot x = I$.

Cycle Notation

Another notation for describing permutations exists -- one that can be a bit easier to both write and type than the matrix form used previously, and which highlights the "cycles" present in a permutation.

To what "cycles" do we refer? Consider the permutation

As examples: $3 \rightarrow 4$ and $4 \rightarrow 7$

Given that one of these two facts tells us what leads to $4$ and the other tells us where $4$ leads, one might be tempted to collapse these two facts into a more compact form, and write $3 \rightarrow 4 \rightarrow 7$ instead.

However, this begs the question: "Where does $7$ then go?" -- which in turn makes us wonder where that number will go. In this case, these next two value are $6$ and $3$, respectively.

We can keep asking where each new value "goes" under this permutation $P$, but a pattern quickly emerges: $$3 \rightarrow 4 \rightarrow 7 \rightarrow 6 \rightarrow 3 \rightarrow 4 \rightarrow 7 \rightarrow 6 \rightarrow 3 \rightarrow 4 \rightarrow 7 \rightarrow 6 \rightarrow \cdots$$

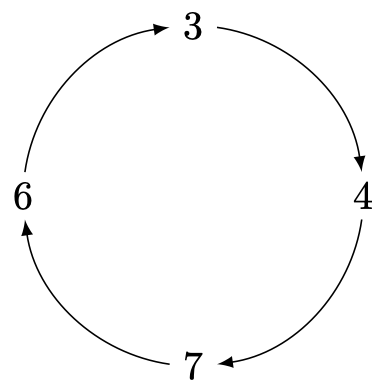
Do you see how the above just "cycles" through the values $3,4,7,6$ over and over, as suggested by the below image?

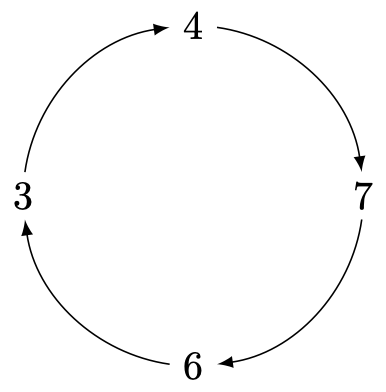
Nicely, regardless of the permutation in question -- if we consider what happens to any number under repeated applications of that permutation, we will ALWAYS see the resulting sequence eventually start to repeat in some cycle as we must eventually run out of values we haven't yet seen, but every number goes somewhere.

Of course, had we started with either $4$, $7$, or $6$ instead, we would have seen the exact same cycle.

Despite our given permutation $P$ containing the cycle discussed above, we haven't yet captured everything this permutation does. There are other values associated with $P$ that "go places" that this cycle doesn't address.

Looking at one of these, say $1$, gives us another cycle: $$1 \rightarrow 2 \rightarrow 1 \rightarrow 2 \rightarrow 1 \rightarrow 2 \rightarrow \cdots$$

The only remaining value not yet considered is $5$, but this too leads to a (trivial) cycle: $$5 \rightarrow 5 \rightarrow 5 \rightarrow \cdots$$

Taking all three cycles together, we can completely represent permutation $P$ with a drawing like the following:

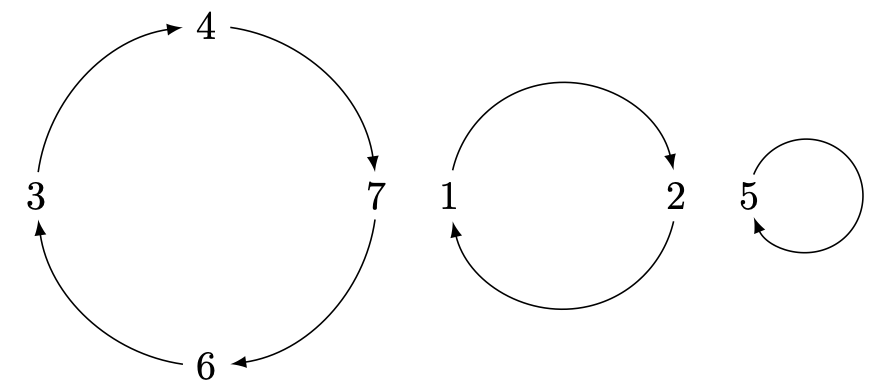
However, representing permutations with drawings like the above will quickly be seen to use too much space on your paper! We can more efficiently identify a permutation using the related cycle notation for the permutation, where we describe each cycle by wrapping the sequence it generates in parentheses. Below, we see the cycle notation for permutation $P$. $$P = (3476)(12)(5)$$

We should be careful, however. The cycle notation for cycles of length more than one can be written in multiple ways. To see this, notice how the two cycles below are absolutely identical in terms of what they send to where, but appear visually different due to a partial rotation,

   

Indeed, we can see that all of the following cycles are equivalent in the same way, as we can similarly "rotate" any one of them by some amount to become any other:

By convention -- unless there is a reason not to do so -- we write cycles so that they start with their smallest value.

As a matter of verbiage, the number of unique values that appear in a cycle before it repeats is known as the length of the cycle. So, for example, the cycles $(3,4,7,6)$, $(1,2)$, and $(5)$ have lengths $4$, $2$, and $1$, respectively.

Note that as long as the number of elements being permuted is clear from the context -- writing cycles of length $1$, like the $(5)$ in the $(3476)(12)(5)$ above is not really needed and we often omit these. Just remember if a number isn't present in a permutation's cycle notation, it "goes to" itself. This adds a little more for us to remember, but saves our pencil lead! 😜

There is one time however, when this convention of not writing any cycles of length $1$ creates a problem. Remember, the identity permutation is the permutation where everybody "goes to" themselves -- and thus, every cycle is a cycle of length $1$. We can't very well write nothing at all for this special permutation! As a work-around, we often denote the identity permutation of $n$ elements either with its own special symbol like the "$I$" used earlier, or something equally unambiguous like "$(1)$", or even just "$()$".

Multiplying/composing permutations written in cycle notation can be easily done -- and without having to first translate them back to their matrix forms. Consider the product of permutations $P = (153)(24)$ and $Q = (12)(345)$, which are each themselves expressed as products of disjoint cycles:

Note viewing each cycle as a permutation in its own right (called a cyclic permutation) we can trivially write the product $PQ$ as a product of four cycles (i.e., $c_1$, $c_2$, $c_3$, and $c_4$), as identified below: $$PQ = \underbrace{(153)}_{c_1} \underbrace{(24)}_{c_2} \underbrace{(12)}_{c_3} \underbrace{(345)}_{c_4}$$

However, we can do better! We can always simplify a product of cycles to either a single cycle or a product of disjoint cycles -- which generally is much shorter to write! A set of cycles are said to be disjoint if no pair of cycles share any common elements. We can find the disjoint cycles in question by tracking what happens to each value (by convention, starting with $1$) under the successive application of each $c_i$, working from left to right.

• $c_1 = (153)$ takes $1$ to $5$;
  $c_2 = (24)$ leaves $5$ unchanged;
  $c_3 = (12)$ leaves $5$ unchanged;
  $c_4 = (345)$ takes $5$ to $3$.
  So $1 \rightarrow 3$ in the product.

• $c_1 = (153)$ takes $3$ to $1$;
  $c_2 = (24)$ leaves $1$ unchanged;
  $c_3 = (12)$ takes $1$ to $2$;
  $c_4 = (345)$ leaves $2$ unchanged.
  So $3 \rightarrow 2$ in the product.

• $c_1 = (153)$ leaves $2$ unchanged;
  $c_2 = (24)$ takes $2$ to $4$;
  $c_3 = (12)$ leaves $4$ unchanged;
  $c_4 = (345)$ takes $4$ to $5$.
  So $2 \rightarrow 5$ in the product.

• $c_1 = (153)$ takes $5$ to $3$;
  $c_2 = (24)$ leaves $3$ unchanged;
  $c_3 = (12)$ leaves $3$ unchanged;
  $c_4 = (345)$ takes $3$ to $4$.
  So $5 \rightarrow 4$ in the product.

• $c_1 = (153)$ leaves $4$ unchanged;
  $c_2 = (24)$ takes $4$ to $2$;
  $c_3 = (12)$ takes $2$ to $1$;
  $c_4 = (345)$ leaves $1$ unchanged;
  So $4 \rightarrow 1$ in the product.

• So in $PQ$ we have $1 \rightarrow 3 \rightarrow 2 \rightarrow 5 \rightarrow 4 \rightarrow 1$, and can thus trivially determine that $PQ = (13254)$. Done! Notice how much shorter $(13254)$ is when compared to that with which we started, $(153)(24)(12)(345)$.

In the above example, the product of $PQ$ reduced to a single cycle. Now consider the product of permutations $R=(125)(34)$ and $S = (123)$, which results instead in a product of disjoint cycles:

Let us work less verbosely than we did a moment ago as tracking through what each cycle (working left to right) does to any given value can easily be done in one's head. Notice that we have $RS = (125)(34)(123)$, and $1 \rightarrow 3 \rightarrow 4 \rightarrow 1$ in the product. Then starting with the (smallest) value unaccounted for -- which is $2$ here, we also have $2 \rightarrow 5 \rightarrow 2$. As such, $RS = (134)(25)$.

Transpositions

Again drawing upon our previous work with braids, let us re-examine the braid that appeared at the beginning of this section -- only this time with the crossings "jiggled" far enough left or right so that no two happen simultaneously as we scan the braid from left to right:

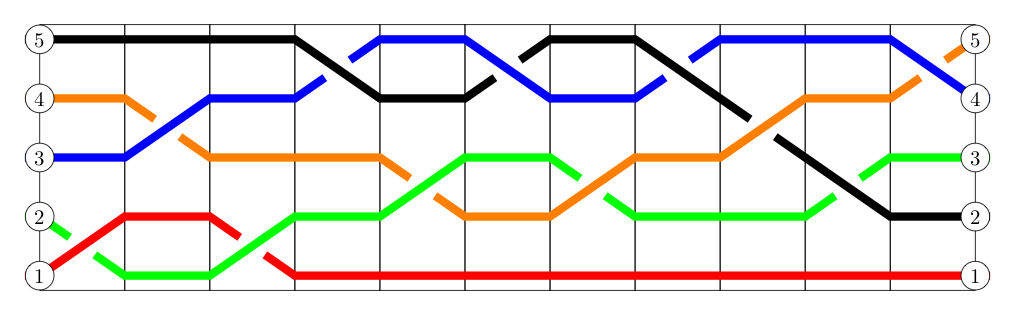
Notice how each individual crossing can be interpreted as a cycle of length $2$, otherwise known as a transposition.

With this perspective, it is easy to write re-write the overall permutation of $5$ elements given as a product of $11$ transpositions:

As it is always possible to find a braid that induces a given permutation, and every braid can be "jiggled" so no simultaneous crossings occur -- it must also be the case that we can always express any given permutation as some sequence of transpositions. In fact, there will always be multiple ways to do this -- with some of these "chains" of transpositions longer than others.

Just in case you are thinking that all we are doing is writing the braids with some new bizarre notation, remember that all of the information about which strand crossed "over" or "under" another in the braid has been lost in the way we write permutations. While elementary braids $x_i$ and $x_i^{-1}$ are different braids, the transpositions $(i,i+1)$ and $(i+1,i)$ are the same transposition. Related to this, again remember that for any single permutation like the one above -- there can be many different, non-equal braids that induce it.

That cautionary comment aside, braids can still help "guide the way" when dealing with permutations.

As an example, we've already noted that permutations, like braids, are not generally commutative. That is to say, if $P$ and $Q$ are both permutations, $PQ$ and $QP$ are not always the same permutation.

However, "distant elementary braids" did commute. We said two elementary braids $x_i$ and $x_j$ were "distant" when $|i-j| \ge 2$, but this was really just a very compact way of saying the two crossings in question didn't involve any strands at the same position.

Of course there is a direct analog to this in the language of transpositions: When transpositions are disjoint (meaning they do not move any common elements), they commute.

Realizing that any cycle can be written as a product of transpositions of pairs of elements that appear in that cycle, the above result can be quickly generalized to the even more powerful rule:

As an example, notice that the calculations below show that the first two cycles commute with each other (they have no common elements), but not the third cycle (which shares a $2$ with the first cycle and a $3$ and $4$ with the second).

The reader may find useful practice in independently finding these four cycle products.

Taking advantage of this property, notice that if a permutation is expressed as a product of disjoint cycles, we can rearrange the cycles however we wish. With this, we often rearrange the disjoint cycles associated with a permutation so that their respective "first elements" (remember, these are the smallest elements "rotated" to the first position) are in ascending order.

For example, $(4,7)(1,6)(2,5,3)$ would typically be rearranged to become $(1,6)(2,5,3)(4,7)$, so that the first elements ($1$, $2$, and $4$) are in ascending order.

This doesn't make how we write the permutation any shorter -- but when combined with the other conventions previously discussed, it provides a way to describe permutations of a known number of elements uniquely. That is to say, if two people describe the same permutation in cycle notation using all these conventions, they will always do so identically.

Commutators

One special type of permutation that will play a very prominent role in our future discussions is called a commutator. A commutator, for our purposes, will be a combination of a special form, that is built from two permutations $p_1$ and $p_2$. Specifically, the commutator of permutations $p_1$ and $p_2$, denoted $[p_1,p_2]$ is defined by $$[p_1,p_2] = p_1 p_2 p_1^{-1} p_2^{-1}$$

As a curious side note, those familiar with the Rubik's cube should know that commutators can play a key role in coming up with a solution to this fun puzzle. Interested readers can check out this YouTube video to learn more about this.

Should it help -- you should know there are a few notational differences between what we have used and what is seen in the video. First, permutations of the colored stickers on the little cubes that result from manipulating the cube are described not in cycle notation or bracket notation, but rather in terms of a sequence of individual actions taken on the cube (e.g., $R$ is a spin of the right side of the cube, clockwise; $D$ is a spin of the side down on the bottom, clockwise). As another difference -- rather than use subscripted variables like $p_1$ and $p_2$, these sequences are then simply refered to by a single number, like $1$ or $2$. Also, instead of expressing compositions of sequences of permutations in a manner similar to how we deal with products, the video uses sums. Lastly, inverses in the video are not expressed with an "exponent" of negative one, but rather with an apostrophe. So, whereas we might write something like $p_1 p_2 p_1^{-1} p_2^{-1}$ to denote a commutator, in the video they use something closer to $1 + 2 + 1' + 2'$ instead.

We can of course use what we know about finding products of permutations to simplify any given commutator to a single cycle or product of disjoint cycles. As an example, let us find the commutator of the two transpositions $(12)$ and $(23)$:

In the aforementioned future discussions we will consider not only commutators, but also commutators of commutators, and commutators of commutators of commutators, etc.

With that in mind, consider the process of finding the commutator of commutators $[[(12),(23)],[(23),(34)]]$ below:

Let us start by finding the first inner commutator, and then the second: $$\begin{array}{l} [(12),(23)] = (123) \quad {\scriptsize \textrm{as previously shown}}\\ [(23),(34)] = (23)(34)(23)^{-1}(34)^{-1} = (23)(34)(23)(34) = (234) \quad {\scriptsize \textrm{after arguing similarly}}\\ \end{array}$$ As such, the outer commutator can be simplified to the following: $$[[(12),(23)],[(23),(34)]] = [(123),(234)]$$ This of course, simplifies further: $$\begin{array}{rcl} [(123),(234)] &=& (123)(234)(123)^{-1}(234)^{-1}\\ &=& (123)(234)(321)(432)\\ &=& (14)(23)\\ \end{array}$$

Expanding Permutation and Cycle Notation

We might occassionally want to permute a set of elements multiple times in the same way, towards some desired end.

For example: when solving the Rubik's Cube puzzle, one often must make the same sequence of moves multiple times -- each of which permutes the stickers on the face of the cube in the exact same way.

Letting $p$ represent a given permutation, we then abbreviate the permutation that results from applying $p$ exactly $a$ times by $p^a$.

This is particularly nice when the permutation in question is a cycle. Notice the patterns in the following:

• $(2,7,4,5,6)^2 = (2,4,6,7,5)$     Since by itself, the cycle being squared moves each element to the element on its right, it's square will do this twice. As such, we simply traverse the cycle two at a time to find the square of the cycle.

• $(1,8,3,2,5,4)^2 = (1,3,5)(2,4,8)$     Doing the same here, notice that we come back to where we started before visiting all of the elements, thus completing one cycle in our simplified form. Starting a new cycle with the smallest element that has not yet been visited, we again traverse two at a time to find the next (and here, the last) cycle of our answer.

• $(1,5,3,2,7,6,4)^3 = (1,2,4,3,6,5,7)$     In a similar way, the cube of a cycle can be found by traversing the cycle three at a time.

• $(1,5,2,3,6,4)^3 = (1,3)(2,4)(5,6)$     Again traversing three at a time, we come back to where we started in this case after only two steps. Each time we do, we close off a cycle and begin with the smallest element not yet visited.

• $(2,6,3,4)^4 = I$     Noting that if we traverse four at a time, each element comes back to where it started!

• $(2,6,3,4)^{10} = (2,6,3,4)^4 (2,6,3,4)^4 (2,6,3,4)^2 = I \cdot I \cdot (2,6,3,4)^2 = (2,3)(4,6)$     Noting the length of the cycle being raised to a power is $4$, we reorganize the ten cycles being composed into as many groups of four as we can, with two remaining. Each composition of four cycles is the identify permutation, so all we have to do is find the product/composition of the last two!

Recalling that for any permutation $p$ we can find an inverse permutation $p^{-1}$ that undoes it (i.e., their composition is the identity permutation $I$), we likewise abbreviate with $p^{-a}$ this inverse permutation applied $a$ times. Note that $p^a$ and $p^{-a}$ are then necessarily inverse permutations of one another.

Here again, if the permutation is a cycle, computing inverses or powers of inverses is quickly done. Consider the following examples:

• $(1,5,2,3,4)^{-1} = (1,4,3,2,5)$     Again the cycle being raised to a power moves each element to the element on its right. Thus, to find the inverse, we simply start with the smallest element (by convention) and traverse the cycle whose inverse we seek by going left instead.

• $(3,7,5,4,8,6)^{-2} = (3,8,5)(4,7,6)$     Combining the strategies already seen, here we start with the smallest element and traverse the cycle being raised to a power by going left (because the exponent is negative), two at a time (given the magnitude of the exponent). Again, when we close off a cycle by returning to an element already seen, we start a new one with the smallest unvisited element (again, by convention).

Following suit with what we did with braids and what many will remember to be true about powers of real values -- and for consistency with the rules to come -- we make two additional definitions for any permutation $p$ (i.e., cycles and non-cycles, alike):

• $p^0 = I$
• $p^1 = p$

With the above abbreviations and definitions, it should be relatively obvious that the following must also hold for permutation $p$ and integers $a$ and $b$:

• $p^a \, p^b = p^{a+b}$         (add exponents when multiplying powers)

• $(p^a)^b = p^{ab}$         (multiply exponents when finding a power of a power)

As an immediate application of how inverses combine (similar to what we saw with braids), we also know

• $p^a \, p^{-b} = p^{a-b}$

When given a product of powers of permutations, we can use the rules described above and the tricks for evaluating powers and products of cycles to simplify things down to either a single cycle or a product of disjoint cycles.

Consider the following example:

Again remembering that the division of one real number by another is equivalent to multiplying the first by the reciprical (i.e., the multiplicative inverse) of the second, we define and denote the "division of one permutation by another" (and the equivalent "fraction of permutations") in the following way: $$p \div q = \frac{p}{q} = p q^{-1}$$

As with braids, doing this leads to more (familiar) results:

• $\displaystyle{p^{-a} = \frac{I}{p^a}}$         (negative exponents are connected to recipricals of powers)

• $\displaystyle{\frac{I}{pq} = q^{-1}p^{-1}}$         (to invert a product, invert each and combine in reverse order)

• $\displaystyle{\frac{p^a}{p^b} = p^{a-b}}$         (subtract exponents when dividing powers)

For permutations that commute, such as disjoint cycles $p$ and $q$ (or inverse pairs, or the identity $I = (1)$ paired with any element, etc), we can say even more!

• $(pq)^a = p^a q^a$         (exponents distribute over products)

• $\displaystyle{\left( \frac{p}{q} \right)^a = \frac{p^a}{q^a}}$         (exponents distribute over quotients)

• If $p_1$, $p_2$, $p_3$, and $p_4$ pairwise commute, then
  
  $\displaystyle{\frac{p_1 p_2}{p_3 p_4} = \frac{p_1}{p_3} \cdot \frac{p_2}{p_4}}$         (quotients of products can be expressed as products of quotients)

Be careful! In dealing with the arithmetic of permutations -- just as was the case when dealing with braid arithmetic -- one needs to only use rules that depend on commutativity when it actually holds!

The following example puts several of these more recent ideas to work: