| | |
Recall that the set of all functions did not form a group under composition, given the problems with identities and inverses. That said, some sets of functions do form groups under composition.
Consider the set of all compositions of functions $f : \mathbb{R} \rightarrow \mathbb{R}$ where $f$ is either:
Recall that all of these individual functions' graphs were lines (as explored in a previous section). Now think about the effect of each action described above when applied to (i.e., composed with) another function whose graph is a line. Each will produce a new function whose graph is still a line!
Consequently, these compositions (in combination with constant functions which also graph as lines) are called linear functions.
We can easily argue that all of these possible compositions are precisely the functions of the form $f(x) = mx + b$, where $m$ and $b$ are real-valued constants.
To see this, consider each function above, and their corresponding $m$ and $b$ values: $$\begin{array}{lcll} f_i(x) = x &\rightarrow& m=1,& b=0\\ f_h(x) = c &\rightarrow& m=0,& b=c\\ f_s(x) = cx &\rightarrow& m=c,& b=0\\ f_r(x) = -x &\rightarrow& m=-1,& b=0\\ f_t(x) = x+c &\rightarrow& m=1,& b=c\\ \end{array}$$ Then note that the composition of any two functions of this form, $f(x) = m_f x + b_f$ and $g(x) = m_g x + b_g$ is clearly expressible in the same form: $$(f \circ g)(x) = m_f(m_g x + b_g) + b_f = (m_f m_g) x + (m_f b_g + b_f) \rightarrow m = m_f m_g, \ b= m_f b_g + b_f$$
Finally, note that every function of the form $f(x) = mx + b$ can be thought of as a scaling function $f_s(x) = mx$ composed with a vertical translation $f_t(x) = x + b$.
Let us call the set of all such functions $\mathscr{L}$. That is to say, $$\mathscr{L} = \{ f(x) = mx + b \ | \ m,b \in \mathbb{R}\}$$ Then recall that for a set to be a group under composition, it must be closed, associative, have an identity, with every element having an inverse in that same set. The general form for a composition of two linear functions found above seems to establish closure, so we might wonder if $\mathscr{L}$ is a group under composition.
Note that with regards to composition, $\mathscr{L}$ inherits associativity from the associativity under composition of the set of all endofunctions on some domain (recall, endofunctions are functions whose domain and codomain agree) -- so that's two of the four properties!
Next, we would ask if the identity function (with domain $\mathbb{R}$) is in $\mathscr{L}$, but of course this is true -- the identity function, $f_i(x)$ is the first function in the list of functions we gave at the start of this section that we started composing together to form $\mathscr{L}$ in the first place!
Lastly, we turn our attention to the existence of an inverse. The astute reader might realize this property is doomed to not hold, as $\mathscr{L}$ includes constant functions, which are not invertible. Sadness!
There is lemonade to be made from that lemon, however!
First, and to set the stage for our analysis of Möbius transformations in the next section, let's re-discover this problem with invertibility in a slightly different way:
Recall that for an inverse to exist, no two distinct inputs $x_1$ and $x_2$ can produce the same output $y$. Equivalently, if $f$ is the function in question, then $f(x_1) = f(x_2)$ implies $x_1 = x_2$.
Suppose for some function $f(x) = mx + b$, that $f(x_1) = f(x_2)$. Then $$mx_1 + b = mx_2 + b$$ To show that $f$ is invertible, we would need to then be able to argue that necessarily $x_1 = x_2$. This is impossible however, unless we know that $m \neq 0$. Sure, we could subtract $b$ from both sides to get $mx_1 = mx_2$, but we won't be able to divide both sides by $m$ to produce $x_1 = x_2$ unless we are assurred $m \neq 0$.
So yes, $\mathscr{L}$ under composition does not form a group. However, that still leaves the door open for some subset of $\mathscr{L}$ to be a group!
Here's the thing -- what if we throw out all the functions with $m=0$? Would the set that's left be a group? With this hope in mind, let us define $$\mathscr{L}_{m \neq 0} = \{ f(x) = mx + b \ | \ m,b \in \mathbb{R} \textrm{ and } m \neq 0\}$$
We earlier showed that when $f(x) = m_f x + b_f$ and $g(x) = m_g x + b_g$ then $(f \circ g) = m x + b$ where $m = m_f m_g$ and $b = m_f b_g + b_f$. Now notice that if $m_f,m_g \neq 0$, then $m = m_f m_g \neq 0$. Thus, $\mathscr{L}_{m \neq 0}$ is closed under composition.
We've already argued that all functions in $\mathscr{L}$ are associative with respect to composition. Note that $\mathscr{L}_{m \neq 0}$ is a subset of $\mathscr{L}$. So all functions within this subset must also be associative under composition as well. Further, the identity function $f(x) = 1 \cdot x + 0 = x$ can clearly be found in $\mathscr{L_{m\neq 0}}$ too.
It remains only to establish that each function in $\mathscr{L}_{m \neq 0}$ has an inverse to establish linear functions form a group under composition. Our earlier argument would suffice to establish that an inverse function exists (given that we can now divide both sides of $mx_1 = mx_2$ by $m$ since we are assured $m\neq 0$). However, we need slightly more than that. We need the inverse function to also be in our set $\mathscr{L}_{m \neq 0}$.
Note that the function $f : \mathbb{R} \rightarrow \mathbb{R}$ described by $f(x) = mx + b$ is identical to the composition $f_t \circ f_s$ where $f_s(x) = mx$ and $f_t(x) = x + b$. As such, $f^{-1} = (f_t^{-1} \circ f_s^{-1})$ by the shoes and socks principle -- implying that $$f^{-1}(x) = \frac{x-b}{m} = \textstyle{\frac{1}{m} x - \frac{b}{m}}$$ Of course, when $m \neq 0$, it must also be true that $\frac{1}{m} \neq 0$. So we see $f^{-1}$ is also in the set $\mathscr{L}_{m \neq 0}$, which was the final piece we needed to establish ${L}_{m \neq 0}$ as a group!
Interestingly, similar arguments can also establish that ${L}_{m \gt 0} = \{f(x) = mx + b \ | \ m,b \in \mathbb{R} \textrm{ and } m \gt 0\}$ is a group.
In the above argument, we found the inverse we needed by seeing $f$ as a composition of simple functions whose inverses were known, and then using the "socks and shoes" principle. But there is another way we could have proceeded.
Suppose $(x,y)$ is any point on the graph of some invertible function $f$ with formula $f(x)$. We have argued before that $(y,x)$ must then be a point on the graph of its inverse, $f^{-1}$. (Recall, we need $f^{-1}(f(x)) = x$, so $f^{-1}(y) = x$)
Thus, if we can deduce what $f^{-1}$ does to an input $y$ to produce the related $x$, we will have a formula for $f^{-1}$. As such, we just solve for $x$ in terms of $y$ in the equation $f(x) = y$.
To keep from confusing which is the input variable and which is the output variable for the result, one might find it more advantageous to simply solve $f(y) = x$. That is to say, swap the $x$ and $y$ in the equation $f(x) = y$ and then solve for the new $y$. This gives us a formula (now in terms of $x$) for $f^{-1}(x)$!
Things are always easier to understand with a concrete example, so consider the following three examples, remembering that once we solve for the new $y$, we have the formula for the corresponding inverse function: $$\begin{array}{r|rcl|rcl|rcl} & f(x) &=& -3x + 2 \quad & \quad g(x) &=& \displaystyle{\frac{x^3 - 2}{7}} \quad & \quad h(x) &=& \displaystyle{\frac{2x + 3}{5x - 4}}&\\\hline & y &=& -3x + 2 \quad & \quad y &=& \displaystyle{\frac{x^3 - 2}{7}} \quad & \quad y &=& \displaystyle{\frac{2x + 3}{5x - 4}} \\\\ {\scriptstyle \textrm{swap $x$ and $y$}} & x &=& -3y + 2 \quad & \quad x &=& \displaystyle{\frac{y^3 - 2}{7}} \quad & \quad x &=& \displaystyle{\frac{2y + 3}{5y - 4}} \\\\ {\scriptstyle \textrm{solve for new $y$}} & x-2 &=& -3y \quad & \quad 7x &=& y^3 - 2 \quad & \quad x(5y-4) &=& 2y+3\\\\ & y &=& \displaystyle{\frac{x-2}{-3}} \quad & \quad 7x + 2 &=& y^3 \quad & \quad 5xy-4x &=& 2y+3\\\\ & f^{-1}(x) &=& \displaystyle{\frac{2-x}{3}} \quad & \quad \sqrt[3]{7x+2} &=& y \quad & \quad 5xy - 2y &=& 4x + 3\\\\ & & & & \quad g^{-1}(x) &=& \sqrt[3]{7x+2} \quad & \quad y(5x-2) &=& 4x+3\\\\ & & & & & & & \quad y &=& \displaystyle{\frac{4x+3}{5x-2}}\\\\ & & & & & & & \quad h^{-1}(x) &=& \displaystyle{\frac{4x+3}{5x-2}}\\ \end{array}$$
We should note that linear functions are pervasive throughout mathematics -- especially calculus, where one of the central problems involves approximating a (potentially much more complicated) function at some given point with a linear one. In particular, we want the original function and its linear approximation near some given point to be virtually indistinguishable from each other. That means that -- near the given point -- their graphs should be at about the same heights and should rise (or fall) at about the same rate.
Interestingly, the rate at which the graph of a linear function rises (or falls) as the input $x$ increases -- which we call the slope of the linear function -- is constant! Unlike every other type of function, this rate-of-change/slope does not depend at all on being near any given point.
To see this, note that if we increase any input $x$ by $h$, the "rise" observed in the graph from $x$ to $x+h$ is in constant proportion to the change seen between the inputs (i.e., $(x+h) - x$), which we frequently call the "run". In fact, if we suppose $f(x) = mx+b$, we see this "rise over run" is not only constant -- it is the value of $m$: $$\begin{array}{rcl} \displaystyle{\textrm{slope} = \frac{\textrm{rise}}{\textrm{run}} = \frac{f(x+h) - f(x)}{(x+h)-x} = \frac{f(x+h)-f(x)}{h}} &=& \displaystyle{\frac{(m(x+h)+b) - (mx+b)}{h}}\\\\ &=& \displaystyle{\frac{mx + mh + b - mx -b}{h}}\\\\ &=& \displaystyle{\frac{mh}{h}}\\\\ &=& m \end{array}$$
This means that we can recover the slope $m$ of any linear function by simply finding the "rise over run" associated with any two points on its graph. Supposing these two points are at $(x_1,y_1)$ and $(x_2,y_2)$, we have: $$m = \frac{\textrm{rise}}{\textrm{run}} = \frac{y_2 - y_1}{x_2 - x_1}$$ We can exploit this fact to find an equation that relates $x$ and $y$ (in the sense of creating a relation) in a way identical to that produced by the function $f(x) = mx+b$, when only knowing a single point on the graph of $f$ and its slope.
Specifically, suppose we know $(x_0,y_0)$ is a point on the graph of some linear function with slope $m$. Then, if $(x,y)$ is any other point on the graph of $f$, then $$m = \frac{y-y_0}{x-x_0}$$ Multiplying both sides by $(x-x_0)$, adding $y_0$ to both sides, and then writing first the side of the equation where only $y$ remains yields: $$y = m(x-x_0) + y_0$$
which we call the point-slope form of the line given the point $(x_0,y_0)$ and slope $m$.Given that the $m$ in a linear function $f(x) = mx + b$ has this nice interpretation as the slope, one might wonder if $b$ represents anything in particular too. Realizing that $f(0) = m \cdot 0 + b = b$, we see that $b$ gives us the $y$-intercept of the graph of the linear function (recalling that a function crosses the $y$-axis when $x=0$).
As two final important points to make about the graphs of linear functions
Let us exclude the case where the two linear functions are identical. (We do this because in geometry a line is never parallel to itself -- but in calculus, redefining things slightly to allow a line to be parallel to itself will be more useful.) To see why the statement above holds for non-identical linear functions, consider the image below which shows the graph of $f(x) = mx + b_1$ (in red) and $g(x) = mx + b_2$ both with a common slope $m$.
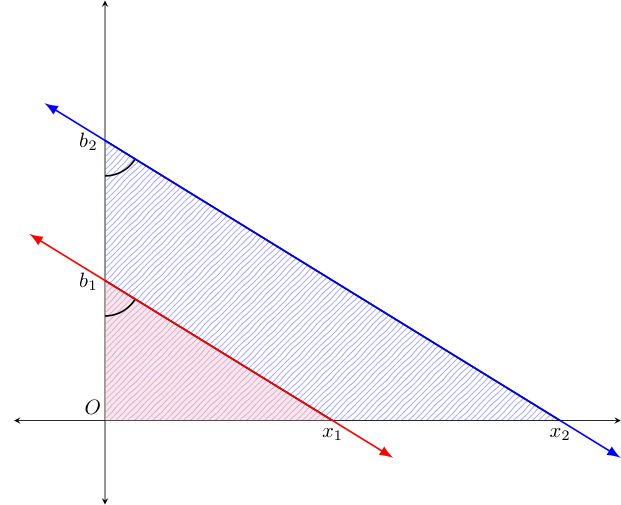
If the slopes are equal, we know the "rise" over the "run" between any two points on the red line or between any two points on the blue line always agree. Thus, $$\frac{b_1}{x_1} = \frac{b_2}{x_2}$$ In this way, we see that corresponding legs of the two right triangles are proportional. Consequently, the two triangles are similar, and thus corresponding angles in these two triangles are congruent. In particular, the two marked angles must be congruent. Noting that the $y$-axis plays the role of a transversal to the red and blue lines, the congruence of these angles tells us the red and blue lines are parallel.
Conversely, if we instead start with the red and blue lines parallel, we can argue the two lines must have the same slope. If the lines are parallel, the two marked angles must be congruent. The angle at $O$ is of course congruent to itself. As both the red and blue triangles are right triangles, we can immediately conclude they are similar -- and thus their corresponding sides are proportional. This means that $b_1/x_1$ = $b_2/x_2$, which tells us the slopes of these two lines agree.
To see this, consider the below image instead. Note that we need only consider lines that intersect at the origin, as shifting perpendicular lines individually up or down by different amounts will not affect the angles formed at their crossing.†
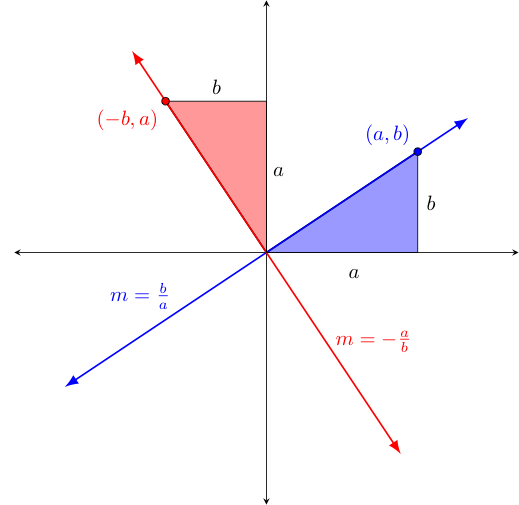
Let us initially assume the slope of the blue line is $m=\frac{b}{a}$ as drawn. The blue triangle is defined by the area bound by the blue line, the line $x=a$, and the $x$-axis. The red triangle is similarly defined by the area bound by the red line, the line $y=a$, and the $y$-axis. We hope to then show that the red and blue triangles will be congruent when the red and blue lines are perpendicular. Doing so allows one to quickly deduce the rest of the distances and coordinates shown -- which then trivially lets one determine the slope of the red line as $-\frac{a}{b}$, the negative reciprocal of the blue line's slope.
The key to proving the congruence of these two triangles given the perpendicularity of the lines rests on first noting the red and blue shaded angles at the origin must be congruent (as they are complements of the same angle between them). Since the two right angles in the shaded triangles must also be congruent, and since the sides between them are congruent by design, the red and blue triangles must be congruent (using the "side-angle-side" congruence theorem).
Alternatively, if the red and blue slopes are negative reciprocals of the form $\frac{b}{a}$ and $-\frac{a}{b}$, we can use the coordinates $(-b,a)$ and $(a,b)$ on the red and blue lines respectively, to establish the triangles. From there, we can again argue the shaded triangles are congruent (but this time due to the fact that the corresponding legs of two right triangles agree). From their congruence, we can establish the shaded angles at the origin agree, and thus the angle between the red and blue lines is identical to that between the $x$ and $y$ axes. This of course means the red and blue lines are perpendicular.
† : A full argument of this would make note that shifting a linear function up or down changes only its $y$-intercept and not its slope -- which means the shifted function is parallel to the original, using the result proven above. Doing this twice leads to two pairs of parallel lines crossing each other. Then, using each as a transversal for the other pair, one can quickly get corresponding angles at each crossing congruent.
We saw in the previous section that linear transformations resulted from compositions of the identity function, scaling functions, reflections over the $x$-axis, and vertical translations.
Then note that the composition of any two functions of this form, $f(x) = \cfrac{a_f x + b_f}{c_f x + d_f}$ and $g(x) = \cfrac{a_g x + b_g}{c_g x + d_g}$ is clearly expressible in the same form: $$\begin{array}{rcl} (f \circ g)(x) &=& \displaystyle{\frac{a_f \left(\cfrac{a_g x+b_g}{c_g x+d_g}\right) + b_f}{c_f \left(\cfrac{a_g x+b_g}{c_gx+d_g}\right) + d_a}}\\\\ &=& \displaystyle{\frac{a_f \left(\cfrac{a_gx+b_g}{c_g x+d_g}\right) + b_f}{c_f \left(\cfrac{a_g x+b_g}{c_g x+d_g}\right) + d_f}} \cdot \cfrac{c_g x+d_g}{c_g x+d_g}\\\\ &=& \displaystyle{\frac{a_f(a_g x+ b_g) + b_f(c_gx+d_g)}{c_f(a_gx+b_g) + d_f(c_gx+d_g)}}\\\\ &=& \displaystyle{\frac{a_f a_gx + a_f b_g + b_f c_g x + b_f d_g}{c_f a_gx + c_f b_g + d_f c_g x + d_f d_g}}\\\\ &=& \displaystyle{\frac{(a_f a_g + b_f c_g)x + (a_f b_g + b_f d_g)}{(c_f a_g + d_f c_g)x + (c_f b_g + d_f d_g)}} \end{array}$$ This tells us that $(f \circ g)(x) = \cfrac{ax + b}{cx + d}$ where: $$a = a_f a_g + b_f c_g, \quad b = a_f b_g + b_f d_g, \quad c = c_f a_g + d_f c_g, \quad \textrm{ and } \quad d = c_f b_g + d_f d_g$$ Finally, note that every function of the form $f(x) = \cfrac{ax + b}{cx + d}$ with $c \neq 0$ is a Möbius transformation as it is the composition of the following $3$ functions: $$\begin{array}{rcll} f_1 &=& x + \frac{d}{c} & \textrm{(a linear function)}\\\\ f_2 &=& \cfrac{1}{x} & \textrm{(the reciprocal function)}\\\\ f_3 &=& \left(\frac{bc-ad}{c^2}\right) x + \frac{a}{c} & \textrm{(a linear function)} \end{array}$$ To see this, consider the work below: $$\begin{array}{rcl} f_3 (f_2 (f_1(x))) &=& f_3 (f_2 (x + \frac{d}{c}))\\\\ &=& \displaystyle{f_3 \left(\frac{1}{x + \frac{d}{c}}\right)}\\\\ &=& \displaystyle{\left(\frac{bc-ad}{c^2}\right) \left(\frac{1}{x + \frac{d}{c}}\right) + \frac{a}{c}}\\\\ &=& \displaystyle{\frac{bc-ad}{c(cx+d)} + \frac{a(cx+d)}{c(cx+d)}}\\\\ &=& \displaystyle{\frac{acx + bc}{c(cx+d)}}\\\\ &=& \displaystyle{\frac{c(ax+b)}{c(cx+d)}}\\\\ &=& \displaystyle{\frac{ax+b}{cx+d}} \end{array}$$ While Möbius transformations are curiously similar to linear functions in terms of how they can be built, they really start to shine when we expand their domains beyond the real numbers. Wait a minute! What set extends beyond the real numbers? Is there such a thing? Is there a set that includes every real value and more?
Ah, that is a story for a future section...