

 |  |
Recall that the arithmetic of integers written in a different base served as motivation for defining polynomials in one variable. While initially considering only polynomials with integer coefficients (i.e., $\mathbb{Z}[x]$), it quickly became apparent upon considering quotients of these that there is value to also studying polynomials whose coefficients are allowed to be rational (i.e., $\mathbb{Q}[x]$). In truth, there is similar value in considering polynomials whose coefficients come from various fields. This includes polynomials with real coefficients, $\mathbb{R}[x]$, and even polynomials with complex coefficients, $\mathbb{C}[x]$!$\newcommand {\cis}{\textrm{cis}\,}$
Notably, as every rational value is real, and every real value is also complex, all of the polynomials we have studied so far could be considered polynomials in $\mathbb{C}[x]$. Although $\mathbb{C}[x]$ includes less familiar polynomials like those below as well. $$x^2 - 2ix - 1$$ $$(1+i)x^3 + (2-i\sqrt{3})x^2 - (\pi-i)x + (3+4i)$$ $$x^4 + (\log_2 3 - i\sqrt[3]{\vphantom{2^2}2})x^3 - (\cis \frac{\pi}{4}) x^2 + ix + \left(\frac{-3+4i\sqrt{5}}{2}\right)$$
Recall the $\cis \theta$ notation seen above (where $\theta = \frac{\pi}{4}$) is just shorthand for : $\cos \theta + i \sin \theta$
Importantly, since we know how to add, subtract, multiply, and divide complex values (except for dividing by zero), we can treat each of the above as a function whose domain and codomain are both $\mathbb{C}$.
We can easily visualize what linear functions in $\mathbb{C}[x]$ do to their inputs by breaking them down into compositions of simple transformations (e.g., translations, scalings, multiplying by $i$ (which rotates the input by $90^{\circ}$), or more generally multiplying by $\textrm{cis}\, \theta$ (which rotates the input by $\theta$ radians) and then considering the net effect of their application in the appropriate order.
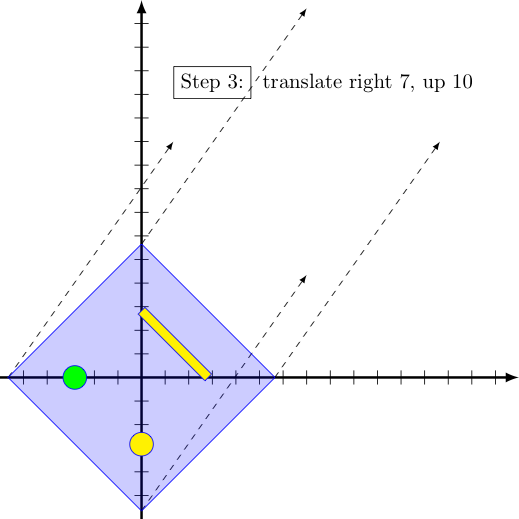
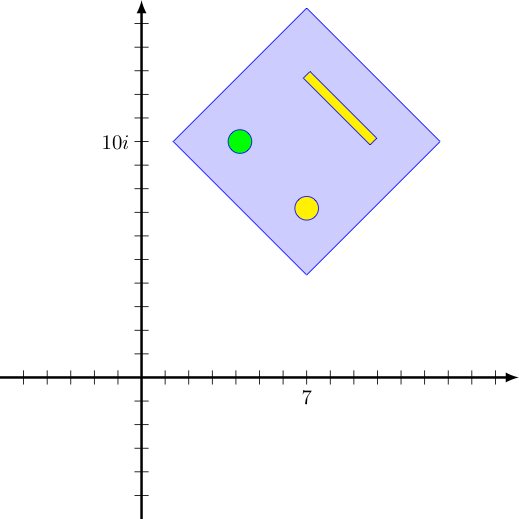
For example, consider the linear function in $\mathbb{C}[x]$ given by $$f(x) = (-\sqrt{2} +i\sqrt{2})x + (7+10i)$$ We will find it advantageous to express the first coefficient (let us call it $z$) in polar form, $r \cdot \cis \theta$, where $r = |z|$ and $\theta = \arg z$.
For our first coefficient $z = (-\sqrt{2}+i\sqrt{2})$, note that we have $$r = |z| = |-\sqrt{2} + i\sqrt{2}| = \sqrt{(-\sqrt{2})^2 + (\sqrt{2})^2} = 2 \quad \textrm{ and } \quad \theta = \arctan \left(\frac{\sqrt{2}}{-\sqrt{2}}\right) + \pi = \frac{3\pi}{4}$$
Note the addition of $\pi$ to the actangent value accounts for the quadrant in which $z = -\sqrt{2} + i\sqrt{2}$ falls.
Recall that multiplying some input $x$ by $z = r \cdot \cis \theta$ both rotates that $x$ by an angle of $\theta$ counter-clockwise about in the complex plane, and scales its distance to zero by $r$. Further, adding a complex value to another translates the second by the real part of the first horizontally and the imaginary part of the first vertically.
As a consequence, the "effect" of our linear function $f$ on any input $x$ is to do the following transformations to it (in order):
We can see the effect of applying these transformations to the inputs that make up the robot face below:
 |
 |
 |
 |
Now let us turn attention to the power functions in $\mathbb{C}[x]$ of degree $2$ or more (i.e., functions $f$ where $f(x) = x^n$ for integers $n\ge 2$), and how they transform points in the complex plane.
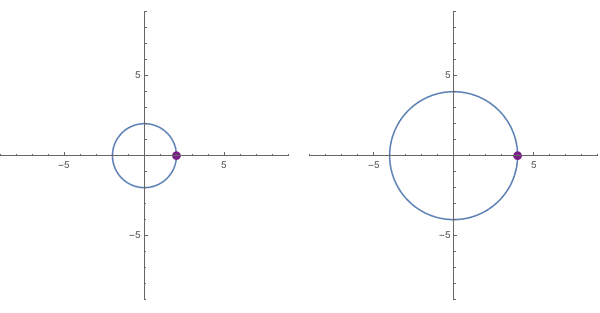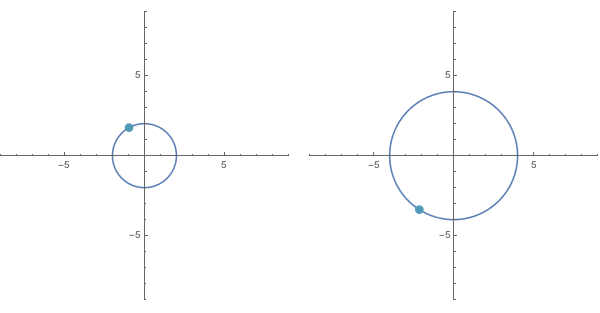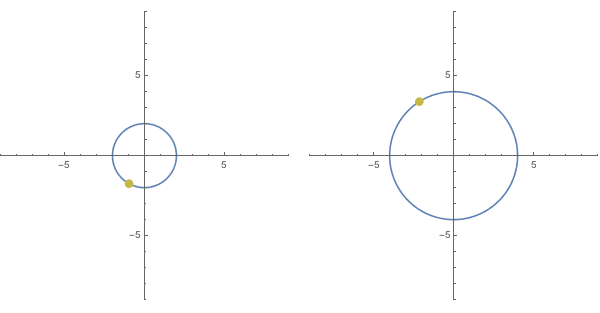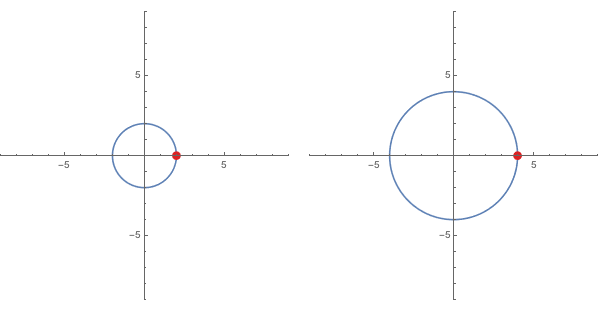
Rather than squaring the complex values whimsically associated with a robot face drawn at the origin (as explored above in the previous section), let us consider squaring the points of the circle $|x|=2$. Recalling that squaring a value both squares its distance to $(0,0)$ and doubles its argument, we can see that the squares of values satisfying $|x| = 2$ (a circle of radius $2$, centered at the origin), must all lie on the circle $|x| = 4$.
However, the angle of rotation associated with any output $x^2$ will always be twice that of the corresponding input $x$. Imagine then, drawing the outputs $x^2$ for each input $x$ encountered when sweeping counterclockwise along this circle $|x|=2$ at some given speed. The output points drawn will then proceed to sweep counterclockwise along $|x| = 4$, but at twice that speed, as shown below:
The cubing function $f(x) = x^3$ works almost identically, except now if the inputs are taken from the circle $|x| = 2$, the outputs will land on the circle $|x| = 8$ and outputs resulting from sweeping one time about the first circle at a given speed rotate about the second circle at three times that speed.
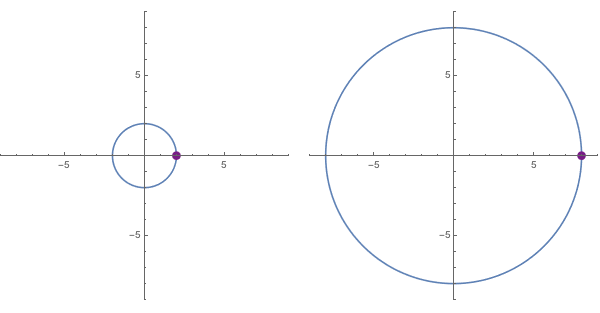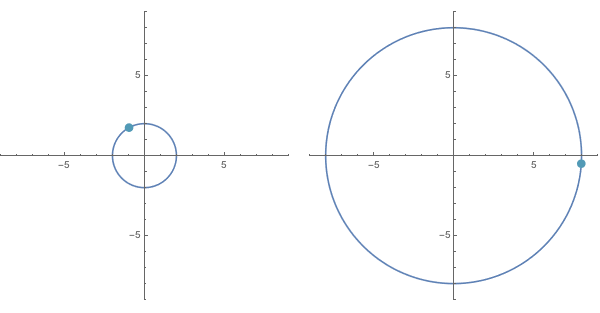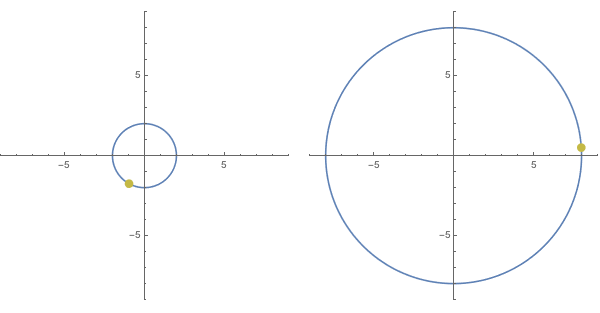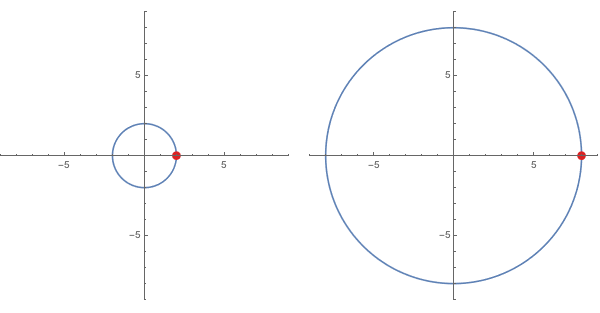
For higher powers, the effects are similar. As the integer exponent $n$ increases for a function $f(x) = x^n$, the outputs corresponding to inputs on $x = |r|$ follow a circle of (exponentially increasing) radius length $r^n$, and for every single revolution of inputs on $x = |r|$ the corresponding outputs sweep out a full revolution on $x = |r^n|$ exactly $n$ times.
Interestingly, the image doesn't qualitatively change much if we consider functions of the form $f(x) = ax^n$ in $\mathbb{C}[x]$ which means $a$ (just like $x$) can be complex. If we again express the coefficient $a$ in polar form, notice that it contributes an extra $(\arg a)$ in rotation and $|a|$ in scaling. While the extra rotation results in a different output for any given single input -- it does not change the image (i.e., set of outputs) of the entire set of inputs on $|x|=r$. To see this, note that rotating a circle centered at the origin leaves it looking the same. The scaling on the other hand, will make the image of the set of inputs on $|x|=r$ farther away (or closer) to the origin by some constant factor. Still, the curve is qualitatively the same -- a circle centered at the origin, when scaled up or down, is still a circle!
Consider for a moment a polynomial function $f : \mathbb{R} \rightarrow \mathbb{R}$ where $f(x) = 2x^3 - 7x^2 + 4x - 6$ and how it compares to the function $g : \mathbb{R} \rightarrow \mathbb{R}$ where $g(x) = 2x^3$, the term of highest degree in $f(x)$. In particular, let's look at their quotient $\frac{f(x)}{g(x)}$ when $x$ is very large -- for example, suppose $x = 1000$: $$\frac{f(1000)}{g(1000)} = \frac{1993003994}{2000000000} \approx 0.996501997 \quad \quad \textrm{ ...a hair's breadth away from the value $1$!}$$ This suggests that while the actual difference between $f(1000)$ and $g(1000)$ may be quite large -- it is miniscule in comparision to the magnitudes of these two values.
This was not an artifact of the particular polynomial or $x$ value we examined either. For any polynomial function $f$, once an input $x$ gets large enough in magnitude (including "large negatives"), the proportion of $f(x)$ that its highest degree term represents is extremely close to one (i.e., "all of it").
To see this, split the quotient into the sum of fractions -- one for each term in $f$. We do this below for the particular $f$ just discussed: $$\begin{array}{rcl} \displaystyle{\frac{f(x)}{g(x)}} &=& \displaystyle{\frac{2x^3 - 7x^2 + 4x - 6}{2x^3}}\\\\ &=& \displaystyle{\frac{2x^3}{2x^3} - \frac{7x^2}{2x^3} + \frac{4x}{2x^3} - \frac{6}{2x^3}}\\\\ &=& \displaystyle{1 - \frac{7}{2x} + \frac{4}{2x^2} - \frac{6}{2x^3}} \end{array}$$ Note in the last expression, the magnitudes of the three right-most terms can be made as small as desired by picking large enough inputs $x$. Consequently, the quotient $f(x)/g(x)$ can be made arbitrarily close to $1$, with sufficiently large $x$.
Given the size discrepency between the single $1$ stemming from $2x^3$ and these other fractional terms (which can be made arbitrarily small for large enough $x$), we say $2x^3$ dominates the other terms of $f(x)$ -- or more simply, that $2x^3$ is the dominant term of $f(x)$.
Nicely, polynomial functions in $\mathbb{C}[x]$ behave the same way! For sufficently large magnitude inputs $x$ (i.e., when $|x|$ is large enough), the value of $f(x)$ will be extremely close (proportionately speaking) to the value of its first term.
Now let's think about what that means for the image of the circle $x=|r|$ for large magnitude complex values $r$ when considering some polynomial function $f(x)$ of degree $n$.
Suppose that $$f(x)=a_n x^n + a_{n-1} x^{n-1} + a_{n-2} x^{n-2} + \cdots + a_0$$ Noting $a_n x^n$ is the dominant term, we expect the image of the set of inputs on the circle $|x| = r$ under application of the function $f$ to be very close to the image of that same set under the application of the function formed by $f$'s leading term: $f_{dom}(x) = a_n x^n$, which as we have seen should be a very large circle centered at the origin.
The other non-dominant terms of $f(x)$ all contribute relatively little to the overall output, proportionately speaking. They will change the image slightly, of course. The "path" swept out $f(x)$ as $x$ travels around the circle of (large) radius $r$ is may slightly deviate a bit left or right, or up or down from the true circular image of $f_{dom}(x)$ -- but we can still expect that as our inputs make one revolution about the origin along a circle of large radius $|r|$, the outputs will go around the origin exactly $n$ times and do so at a much greater distance from that central point (i.e., close to $|a_n| \cdot r^n$).
As being able to see a concrete example almost always helps, consider the image of $|x|=5$ upon application of the polynomial $f(x) = (2-i)x^3 + (\sqrt{2}-5i)x^2 -(7-\pi i)x + (20-30i)$:
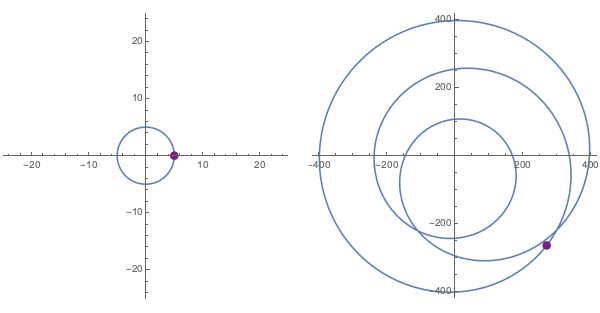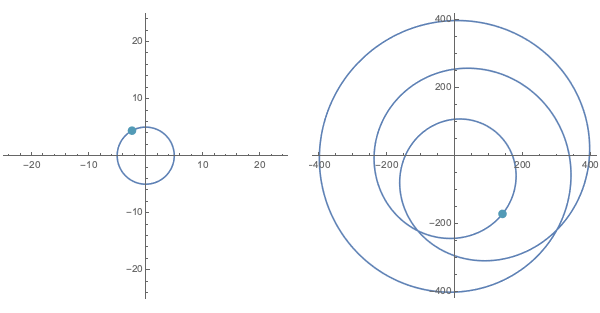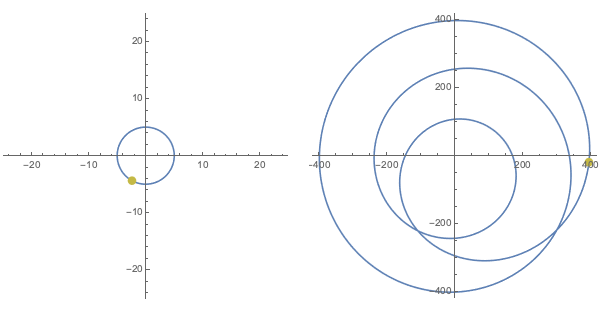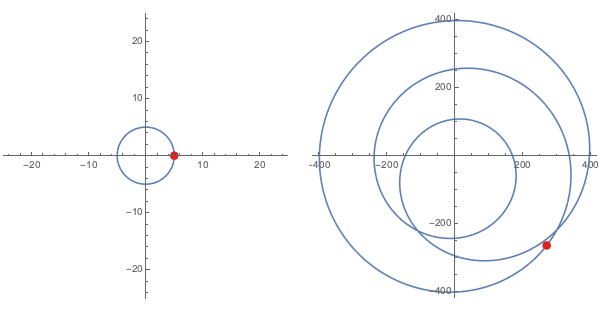
Notice what $f(0)$ is for this last polynomial. Plugging $x=0$ into $(2-i)x^3 + (\sqrt{2}-5i)x^2 -(7-\pi i)x + (20-30i)$ makes all of the terms vanish, with exception of the constant at the end. Indeed, for any polynomial this would be the case. $f(0)$ always yields the constant term.
Now imagine that we start with a set of inputs on a circle of radius large enough to contain both this constant term and zero (i.e., the origin). As we can see even above, the points on the circle of radius $5$ (i.e. $|x|=5$) suffices for this particular function $f$.
Now imagine shrinking the radius of this set of inputs until the circle of inputs becomes a point at $0$. The "path" of the resulting outputs should then also continuously contract down to a single point corresponding to the constant term of the polynomial in question.
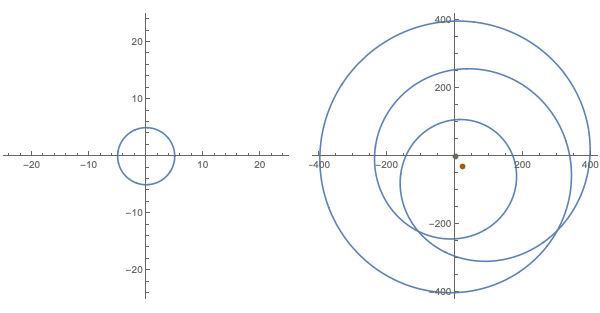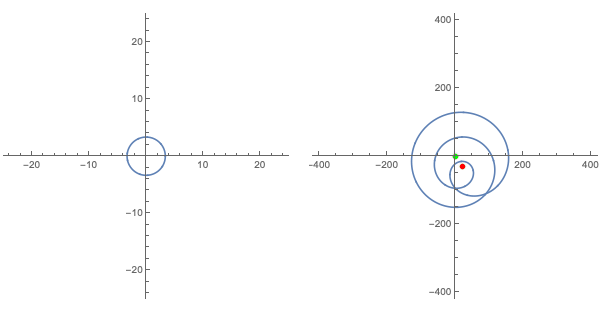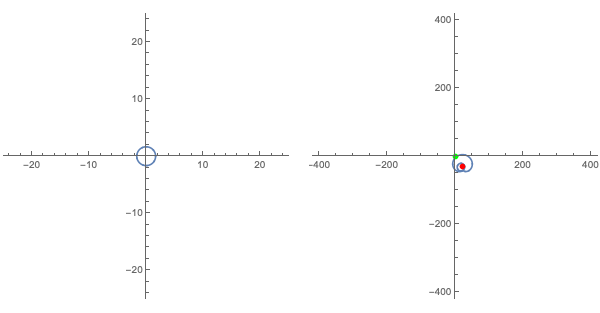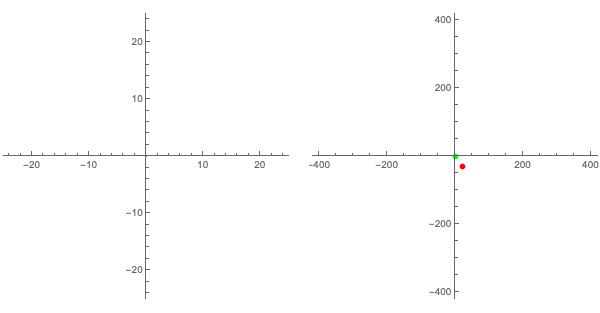
Note the points corresponding to the constant term and the origin are marked above in red and green, respectively. Recall that we chose our initial circle of inputs large enough that the dominance of the first term for large magnitude inputs would keep the impact of the other terms small enough that both the green and red dots were within the winding "path" of corresponding outputs.
Noting that the "path of outputs" is continuous everywhere (i.e., there are no holes or gaps in it with which we could get to one side of the path from the other without intersecting it), consider what happens to this path of outputs as it contracts to become arbitrarily close to the constant term, there must be a moment where it intersects the green dot. At that moment, there must be an $x$ on the input circle where $f(x)=0$. This $x$ is thus a root of the polynomial. This establishes one of the most important results in mathematics:
Of course, as soon as we know one root $r_1$ to $f(x)$ exists, we know the factor $(x-r_1)$ evenly divides $f(x)$. Their quotient must then be a polynomial function as well, but of one less degree. You can probably see where this is going -- we can apply the Fundamental Theorem of Algebra to this smaller degree polynomial, and then again to an even smaller degree polynomial, etc. to discover more and more roots to $f(x)$ -- until at last the quotient is some constant value $a$, and no further factorization can be done.
If $f(x)$ was an $n^{th}$ degree polynomial, we can thus find $n$ factors of the form $(x-r_i)$ so that $f(x)$ can be factored as $$f(x) = a(x-r_1)(x-r_2)(x-r_3)\cdots(x-r_n)$$ Defining the multiplicity of a factor in a product to be equal to the number of times that factor appears, we can then also state with confidence the following important corollary to the Fundamental Theorem of Algebra: