

 |  |
There is something discovered almost immediately upon playing around with solving quadratic equations that don't factor "nicely" (i.e., as products of polynomials with integer coefficients) -- regardless of which technique used to solve them. There seems to be a lot of quadratic equations whose solutions are annoyingly not real numbers! As two examples, consider the following quadratic equations: $$\begin{array}{rcl} x^2 + x + 1 = 0 \quad &\longrightarrow& \quad x = \cfrac{-1 \pm \sqrt{-3}}{2}\\ 2x^2 - 5x + 4 = 0 \quad &\longrightarrow& \quad x = \cfrac{5 \pm \sqrt{-7}}{4} \end{array}$$ We know of course, that no real number squared can give a negative like $-3$ or $-7$ above.
We could look at countless other examples -- and we would notice that every time the solution is not real, a negative under a square root is to blame.
Indeed, we could even lay the entirety of the blame for these "non-real" solutions upon a single thing -- the simple lack of existence of $\sqrt{-1}$.

Not sure what to make of this $\sqrt{-1}$, let us take a cue from the great Russian-French mathematician and leading figure in the creation of modern algebraic geometry, Alexander Grothendieck. With a habit of seeing "the act of naming mathematical objects as an integral part of their discovery, as a way to grasp them even before they have been entirely understood", as written by one observer -- Grothendieck would undoubtedly encourage us to first give this non-real value a name! Hoping that doing so stirs our imagination to a point where we can make sense of this strange value, let us say that $$i = \sqrt{-1}$$ Note that we can now argue if only the value $i$ truly existed, all of the aforementioned "problem solutions" would essentially go away. For example, the solutions to the quadratics given above could both be written in terms of $i$ in the following way: $$x = \frac{-1 \pm i\sqrt{3}}{2} \quad \textrm{and} \quad x = \frac{5 \pm i \sqrt{7}}{4}$$
Of course, imagining a world where this value of $i$ existed will require acknowleging some other basic consequences. Things like the aforementioned solutions and other (more complicated) combinations will also need to exist. We don't want to cripple the real numbers by its addition, after all. Indeed, we want to preserve all of the properties that the real numbers enjoy. That is to say, if we can imagine a new set of numbers -- to which both $i$ and all the real numbers belong -- we would want this new, larger set of numbers to form a field with respect to addition and multiplication!
In this light, we can see that if we define the value of $i$ to be some (non-real) number where $i^2 = -1$, then what we are actually contemplating is simply the extension field $\mathbb{R}(i)$.
Much like how adding $\sqrt{2}$ to the rationals required expanding the rationals to $Q(\sqrt{2}) = \{ a + b\sqrt{2} \ | \ a,b \in \mathbb{Q} \}$ in order to preserve the properties of a field, we can argue that $\mathbb{R}(i) = \{ a + bi \ | \ a,b \in \mathbb{R} \}$, calling this field extension the set of complex numbers, denoting this set by $\mathbb{C}$.
For every complex number $z = a + bi$, we further refer to the value of $a$ as the real part of $z$, denoting this by $Re(z)$. The real value $b$ we call the imaginary part of $z$, denoting this by $Im(z)$. Similarly, numbers of the form $z = 0 + bi$ (i.e., complex numbers without a real part, are called imaginary numbers.
Ensuring that $\mathbb{C}$ as described above, actually is a field is fairly straight-forward. Below, we highlight how it satisfies some of the more interesting requirements, leaving the remainder to be verified by the reader.
Closure: Note of course that $\mathbb{C}$ must be closed under addition and multiplication, as the sum and product of any two complex numbers can be expressed in the form $(a+bi)$ where $a$ and $b$ are both real values, as $$\begin{array}{ccl} (a_1 + b_1 i) + (a_2 + b_2 i) &=& (a_1 + a_2) + (b_1 + b_2) i \quad \textrm{ and }\\\\ (a_1 + b_1 i) \cdot (a_2 + b_2 i) &=& a_1 a_2 + a_2 b_1 i + a_1 b_2 i + b_1 b_2 i^2\\ &=& a_1 a_2 + a_2 b_1 i + a_1 b_2 i - b_1 b_2\\ &=& (a_1 a_2 - b_1 b_2) + (a_2 b_1 + a_1 b_2) i \end{array}$$
Commutativity: Many properties, like the commutativity of addition and multiplication of complex values, result from the same property enjoyed by the field of (only) real values. As an example, suppose we wish to show $z_1 + z_2 = z_2 + z_1$ and $z_1 \cdot z_2 = z_2 \cdot z_1$. Assuming that $z_1 = a_1 + b_1 i$ and $z_2 = a_2 + b_2 i$, we have $$\begin{array}{rcl} z_1 + z_2 &=& (a_1 + b_1 i) + (a_2 + b_2 i)\\ &=& (a_1 + a_2) + (b_1 + b_2)i\\ &=& (a_2 + a_1) + (b_2 + b_1)i \quad \textrm{by commutativity with respect to addition in $\mathbb{R}$}\\ &=& z_2 + z_1 \quad \textrm{ and }\\\\ z_1 \cdot z_2 &=& (a_1 + b_1 i) \cdot (a_2 + b_2 i)\\ &=& (a_1 a_2 - b_1 b_2) + (a_2 b_1 + a_1 b_2) i\\ &=& (a_2 a_1 - b_2 b_1) + (a_2 b_1 + a_1 b_2) i \quad \textrm {by commutativity with respect to multiplication in $\mathbb{R}$}\\ &=& (a_2 a_1 - b_2 b_1) + (a_1 b_2 + a_2 b_1) i \quad \textrm {by commutativity with respect to addition in $\mathbb{R}$}\\ &=& (a_2 + b_2 i) \cdot (a_1 + b_1 i)\\ &=& z_2 \cdot z_1 \end{array}$$
Additive Inverses: Additive inverses in $\mathbb{C}$ follow naturally from $0$ still serving as the additive identity. Denoting the additive inverse of a compex value $z = a + bi$ in the usual way as $-z$, we see this value must be $-z = -a + (-b)i = -a - bi$, as $$(a + bi) + (-a - bi) = (a-a) + (b-b)i = 0 + 0i = 0$$
Multiplicative Inverses for Non-Zero Values: Multiplicative inverses in $\mathbb{C}$ can be found similar to those in $\mathbb{Q}(\sqrt{2})$. We use the "conjugate trick", as can be seen below for $z = a + bi$ below: $$z^{-1} = \frac{1}{z} = \frac{1}{a+bi} = \frac{1}{a+bi} \cdot \frac{a-bi}{a-bi} = \frac{a-bi}{a^2 - (bi)^2} = \frac{a-bi}{a^2 + b^2} = \left(\frac{a}{a^2 + b^2}\right) - \left(\frac{b}{a^2 + b^2}\right) i$$ Note, as long as $z \neq 0$ (i.e., not both $a$ and $b$ are zero), then the denominators on the far right will not be zero. As such, both the real part and the coefficient on the imaginary part of $z^{-1}$ will be real, as required.
As it turns out, the conjugate of a complex number $z = a+bi$ is useful in a great variety of circumstances -- and thus earns its own notation. In particular, if $z = a + bi$, then its conjugate is $\overline{z} = a -bi$
Armed with the expressions appearing in the closure argument above, and the means for finding additive and multiplicative inverses also previously described, we can perform all of the basic operations formerly seen in the real numbers: addition, subtraction (i.e., addition of an additive inverse), multiplication (i.e., repeated addition), division (i.e., multiplication by the multiplicative inverse of a non-zero value), exponentiation (i.e., repeated multiplication), etc.
We often visualize the real numbers as associated with points on a line (called the real number line). However, if the complex numbers involve non-real values of the form $z=a+bi$, which consequently can't be associated with any point on the real number line, how can we visualize them? A good answer to this question is hinted at by exploring the following question:
Of course the simplest answer to this question is that we get the following product: $$(a + bi) \cdot i = -b + ai$$ However, if we go a bit deeper we can connect the result above with something else we've seen. Notice what happened to the real and imaginary coefficients -- they swapped positions, and one was negated. Does that sound familiar? Do you recall the below diagram formerly used in our discussion of when the graphs of two linear functions would be perpendicular (i.e., when their slopes were negative reciprocals of one another)? Look closely at the two ordered pairs in this diagram. Thinking about how to produce the red coordinates $(-b,a)$ from the blue ones $(a,b)$, do you see how we simply swapped the $a$ and the $b$, and negated one of these (i.e., the $b$)?
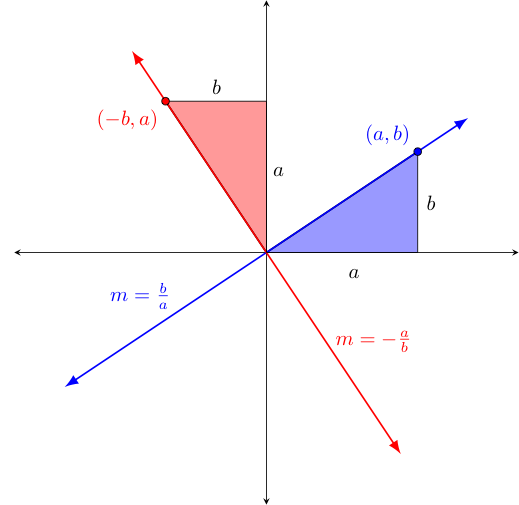
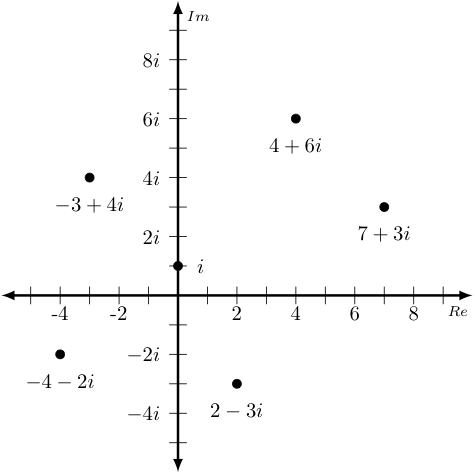
Interestingly -- in answering this question, we seem to have uncovered some connection between a complex number $z = a+bi$ and the coordinates $(a,b)$. Wouldn't it be nice if we could just identify each complex number $a + bi$ with the point whose coordinates are $(a,b)$ in a coordinate plane? Let's do just that, although while we are at it, let us also rename the $x$ and $y$ axes, referring to them now the real and imaginary axes ($Re$ and $Im$, for short). The result we call the complex plane, as shown below (with a sample of a few complex values plotted upon it):
Much like we did with functions that operate on real numbers, we will find it useful to be able to visualize simple functions operating on complex values as graphical transformations. Perhaps surprisingly, many of the simple real-valued functions previously examined have direct complex-valued function analogs. We discuss some of the more important of these below.
Note, just as functions whose input variables are specified by the letter $x$ (e.g., $f(x), g(x),$ etc.) are assumed by default (in the absence of an explicit domain and codomain identified) to take real numbers to other real numbers -- there is a tradition where we similarly assume (unless otherwise instructed) that a function whose input variable is a $z$ takes complex-values to complex values.
Translations
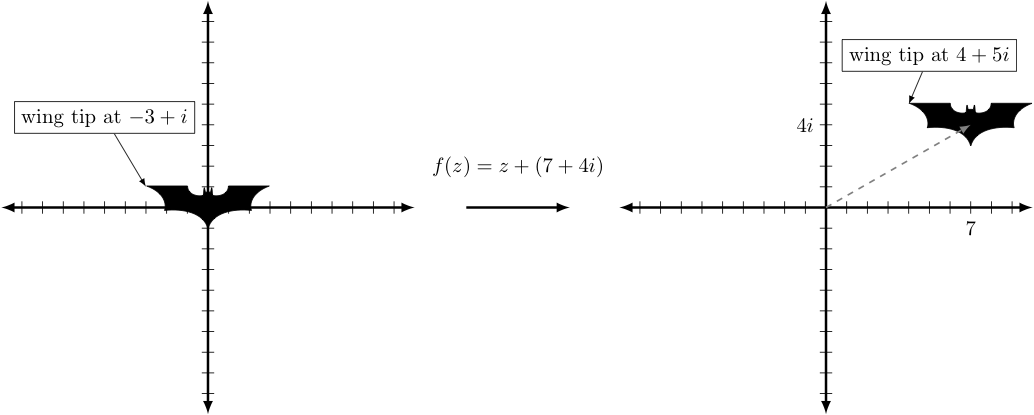
Consider the effect of the function $f(z) = z + z_c$ where $z_c$ is some constant complex value. Similar to how $f(x) = x + c$ could be used to shift inputs either up or down by some fixed distance, $f(z)$ can be used to shift its complex inputs any direction by some fixed distance.
Consider the below example, where we translate every point $z = a+bi$ of a bat shape in the domain on the left to the corresponding value of $f(z)$ where $f(z) = z + (7 + 4i)$ to form the image on the right. Note this means for each such $z$, we have $f(z) = (a+7) + (b+4)i$. Hence, we move all of these points to the right $7$ units and upwards $4$ (imaginary) units:
Scalings
Now consider the result of applying $f(z) = cz$ (where $c$ is a positive real value) to some complex value $z = a+bi$. As before, the output is easily found to be $cz = c(a + bi) = ca + cbi$.
Graphically though, we can interpret this as the result of "scaling" both the real and imaginary parts by $c$. Consequently, we are scaling up (if $c \gt 1$) or down (if $0 \lt c \lt 1$) the distance between each $z$ and $0$, as seen in the images below.

Reflections
Considering $f(z) = -z$ now, we see that for $z=a+bi$ we have $f(z) = -(a+bi) = -a-bi$. Here too, we see a nice way to interpret this action visually -- one very consistent with what happened with the corresponding function when applied to a domain of just real values.
Recall that negating a real value $x$ reflected that value across zero on the real number line to produce the other value on that line at equal distance to zero. Negating a complex value $z$ does the exact same thing, except we now have different lines involved for each such $z$ -- with these all extending radially from zero (i.e., $0 + 0i$).
One can see this happen when $f(z) = -z$ is applied to complex values corresponding to the graph of the rainbow-legged spider on the below left. Notice that all of the points of the different colored legs are "reflected" across zero (i.e., the center of the spider's body) to a similarly colored point in output image on the right.
As a specific case, consider the point at the spider's "red knee". Notice how the reflection of this point shows up on the line connecting this point and $0$ (drawn as a thick gray strip) but on the other side of $0$, and at equal distance from it.
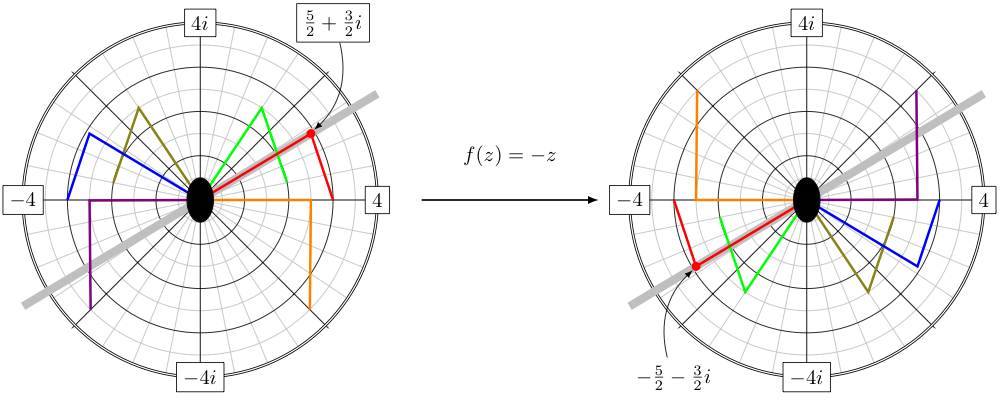
Collectively, there is another way to interpret the action of this transformation. Notice that the spider above has been rotated by $180^{\circ}$, counterclockwise about $z=0$. In general, this is true. That is to say, $f(z)=-z$ always rotates the points $z$ to which it is applied counter-clockwise halfway around the origin.
Recall that for $x \in \mathbb{R}$, one way we can define $|x|$ is in a piecewise way by focusing on the effect that absolute value has on its input (i.e., it "makes it a positive"). However, this definition proves insufficient for complex values, as we now have two real values associated with each complex number -- the real part and the imaginary coefficient -- which could be either both positive, both negative, or some mixture of these.
Instead, defining absolute value for both real and complex values as the distance to zero will be much more beneficial. Recall that distance, by its very nature must also be a positive real value, and this more general definition leaves the absolute value of any real number unchanged from what it was under our old definition.
While we choose not to go into the details here -- there are actually different ways that one can measure the "distance" between two points. These are called metrics. Suffice it to say, adopting the Euclidean metric (i.e., the traditional way to calculate distances in a coordinate plane) and using the same to find the distance between $(a,b)$ and $(0,0)$ will have some particular niceties when it comes to defining $|z|$ for some $z = a+bi$ (especially as it relates to multiplicative inverses of complex numbers as previously computed).
Recalling the distance formula, $d = \sqrt{(x_1 - x_0)^2 + (y_1 - y_0)^2}$ (derived from the Pythagorean theorem) that calculates the distance $d$ between two points $(x_0,y_0)$ and $(x_1,y_1)$ on a coordinate plane -- we see that for points $(a,b)$ and $(0,0)$, we have $d = \sqrt{(a-0)^2 + (b-0)^2} = \sqrt{a^2 + b^2}$.
As such, we define $|a + bi|$ to equal $\sqrt{a^2 + b^2}$, calling this either the absolute value, magnitude, or modulus of $a + bi$, depending on the circumstances at hand -- the last being a dimunitive form of the Latin modus, which means "measure".
While it may appear unrelated for a brief moment -- let us consider the set of complex values of unit magnitude (i.e., complex values $z = a + bi$ with $|z| = 1$). As the set of all points equidistant from a given point in a plane forms a circle, and the corresponding ordered pairs $(a,b)$ for all such $z$ are at unit distance from $(0,0)$, these $z$ must exist on a circle of radius $1$ centered at the origin. Let us call this the unit circle in the complex plane.
Note that we can scale any complex value (except $0$) so that the result lands on the unit circle. Unsurprisingly, we accomplish this by dividing the complex number by its magnitude. So for any complex $z \neq 0$, $z/|z|$ has unit magnitude and thus falls on the unit circle.
Let us consider for each complex $z$ an angle $\theta$ through which the value $1$ (i.e., located at the intersection of the positive real axis and the unit circle) can be rotated counter-clockwise to "land on" the line from zero to $z$. Let these angles be denoted by the argument* of $z$, or more even simply as $\arg(z)$.
Since it is possible to rotate more than one full rotation (i.e.., more than $360^{\circ})$, we should acknowledge that there are many angles $\theta$ associated with any given complex value $z$ on the unit circle. Interestingly, we have seen such phenomena before -- recall the many passages of time that could be associated with a single position of the hand of a clock in our previously discussed clock arithmetic!
Beyond these larger values, we might also generalize our notion of "angle" by allowing them to be negative too -- since rotation about a point can be done in two directions in the plane (i.e., both clockwise and counter-clockwise). As a standard, we associate positive $\theta$ with counter-clockwise rotations and negative $\theta$ clockwise rotations.
As an important consequence, note that a rotation of the complex value $1$ about the origin by an angle of $-\theta$ "lands" in the same place as when we rotate it by $360^{\circ}-\theta$.
When rotating the complex number $1$ about $0$ (the origin) in the complex plane by two different angle measures both "land" in the same place, we say these two angles are co-terminal. The picture below shows three angles, each of which is co-terminal to the other two. More generally, for any integer $n$, angles $\theta$ and $\theta + n \cdot 360^{\circ}$ will be co-terminal to each other.
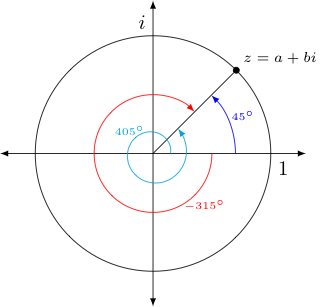
Given the above discussion, note that $\arg(z)$ should technically be thought of as a function in the same sense that Peano's $\sqrt[n]{{}^{*}{x}}$ is a function (recall this gives all the $n^{th}$ roots of $x$, not just the principle $n^{th}$ root. The output of $\arg(z)$ is in actuality a set of multiple values, as opposed to a single value.
That said, we will be intentionally "loose" with what we mean when we write $arg(z)$ -- sometimes pretending that we are just working with one of the angles in $arg(z)$, when we know that any of the angles in that set would behave similarly.
Armed with all of the above, we can now explore the geometric effect of complex multiplication more generally.
Recall that the first thing we explored with regard to the geometry of complex numbers was what 'happened' graphically to a complex value $a+bi$ when we multiplied it by $i$. We discovered a connection to perpendicular lines. To remind ourselves of how that manifest, consider the following diagram which is very similar to the one we considered in that earlier discussion, but is now drawn on the complex plane, under the additional assumption that $z=a+bi$ is on the unit circle and thus has unit magnitude:
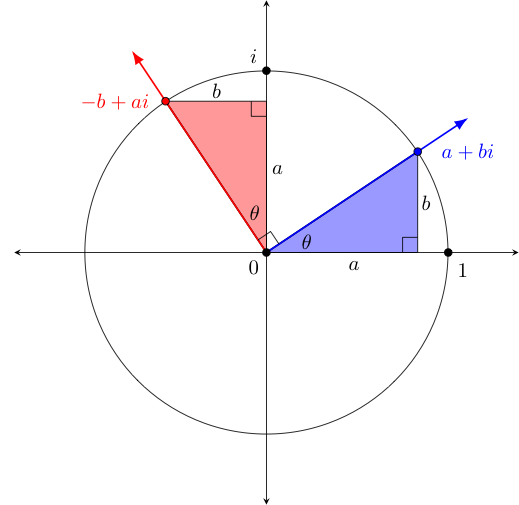
When previously considered, we had noticed that $z_1 = a+bi$ when multiplied by $i$ became $z_2 = -b + ai$. As the slopes of the red and blue lines are negative reciprocals $\frac{b}{a}$ and $-\frac{a}{b}$ respectively, we concluded they must be perpendicular to one another.
Given this fact and that $i \cdot (a+bi) = -b+ai$ falls in the second quadrant when $a+bi$ is in the first, we can interpret this to mean that when multiplying a complex number $z$ by $i$, the result is $z$ rotated counter-clockwise by $90^{\circ}$.
Now however, let us turn this on its head and consider the same diagram above, arguing what the effects are on both $1$ and $i$ when they are multiplied by some unit magnitude $z = a+bi$.
Suppose $z = a + bi$ is on the unit circle. We know know $1 \cdot z = z$ and supposing $\theta$ is an angle in $\arg(z)$ (like that shown in the blue triangle), then we can interpret this multiplication of $1$ by a unit magnitude $z$ as rotating $1$ counter-clockwise by $\theta$.
Similarly, note that $i$ is also on the unit circle, and the red and blue triangles must be congruent (as they are right triangles with corresponding legs congruent). Consequently, the angle in the red triangle with its vertex at $0$ must also measure $\theta$. Thus, we can interpret the multiplication of $i$ by a unit magnitude $z$ as also rotating $i$ counter-clockwise by that same $\theta$ in $\arg(z)$.
Now, let us put all this together...
Suppose we want wish to see how to find $z_1 \cdot z_2$ for two arbitrary non-zero complex numbers. (If either were zero, their product is of course zero.)
Just to put names on a bunch of different relevant pieces: Let $\theta_1$ be in $\arg(z_1)$ and $\theta_2$ be in $\arg(z_2)$, and then define $z_{\theta_1} = \frac{z_1}{|z_1|}$ and $z_{\theta_2} = \frac{z_2}{|z_2|}$, noting that both $z_{\theta_1}$ and $z_{\theta_2}$ are unit magnitude complex values that have arguments matching those of $z_1$ and $z_2$ respectively.
Let the function $\textrm{rot}_{\theta}(z)$ signify the result of rotating any complex $z$ by $\theta$ counter-clockwise about zero. Lastly, suppose $z_{\theta_2} = a_2 + b_2 i$.
Then note that $z_1 = |z_1| \cdot z_{\theta_1}$ and $z_2 = |z_2| \cdot z_{\theta_2}$, so that we have $$\begin{array}{rcl} z_1 \cdot z_2 &=& (|z_1| \cdot z_{\theta_1})(|z_2| \cdot z_{\theta_2})\\ &=& |z_1| \cdot |z_2| \cdot z_{\theta_2} \cdot z_{\theta_1}\\ &=& |z_1| \cdot |z_2| \cdot (a_2 + b_2 i) \cdot z_{\theta_1}\\ &=& |z_1| \cdot |z_2| \cdot (a_2 \cdot z_{\theta_1} + b_2 z_{\theta_1} i)\\ &=& |z_1| \cdot |z_2| \cdot (a_2 \cdot \textrm{rot}_{\theta_1}(1) + b_2 \cdot \textrm{rot}_{\theta_1}(i))\\ &=& |z_1| \cdot |z_2| \cdot (\textrm{rot}_{\theta_1}(a_2) + \textrm{rot}_{\theta_1}(b_2i)) \quad \quad {\Tiny \textrm{(upon considering "Note 1", below)}}\\ &=& |z_1| \cdot |z_2| \cdot \textrm{rot}_{\theta_1}(a_2 + b_2i) \quad \quad {\Tiny \textrm{(upon considering "Note 2", below)}}\\ &=& |z_1| \cdot |z_2| \cdot \textrm{rot}_{\theta_1}(z_{\theta_2})\\ &=& |z_1| \cdot |z_2| \cdot \textrm{rot}_{\theta_1}(\textrm{rot}_{\theta_2}(1))\\ &=& \underbrace{|z_1| \cdot |z_2|}_{\textrm{notably in $\mathbb{R^+}$}} \cdot \textrm{rot}_{(\theta_1 + \theta_2)}(1) \end{array}$$
Note 1: Rotation and scaling are independent operations. That is to say, if we rotate a point about the origin by some amount and then increase its distance to zero by some factor (e.g., doubling it, tripling it, etc), we end up in the same place as if we increased the distance from the original point to zero by that same factor and then rotated it by the same amount. Nicely, the order of application doesn't matter!
Note 2: Rotating the sum of two complex values by some $\theta$ similarly leaves one in the same place as summing the complex numbers that result from rotating each of the original values by $\theta$ as well. Again, the order doesn't matter here!
Importantly, consider the implications of the above for the magnitude and argument of the product of $z_1 \cdot z_2$.
Clearly, $z_1 \cdot z_2$ can be found by rotating $1$ about the origin by an angle equal to the sum of the arguments of $z_1$ and $z_2$, and then scaling the result by $|z_1| \cdot |z_2|$. This means the distance from zero to $z_1 \cdot z_2$ must be the product of their magnitudes, and the argument for $z_1 \cdot z_2$ is the sum of their arguments!
That is to say:
|
For any non-zero complex numbers, $z_1$ and $z_2$, $$|z_1 \cdot z_2| = |z_1| \cdot |z_2| \quad \quad \textrm{ and } \quad \quad arg(z_1 \cdot z_2) = arg(z_1) + arg(z_2)$$ |
From there, we can deduce the "effect" of multiplying a complex value $z_1$ by a complex value $z_2$ is to rotate $z_1$ about the origin by $\arg(z_2)$ and then scale the result by $|z_2|$.
* : The term argument appears to have its origin in a term used by astonomers when referring to an angle of a planetary body in orbit around another (this having obvious connections to a point moving along a circle about the origin in a coordinate plane). Why astronomers chose this word is less clear. The earliest citation given in the Oxford English Dictionary is from Chaucer, circa 1391: "To knowe the mene mote and the argumentis of any planete" (Astrol. xliv. 54).