

 |  |
Having previously looked at raising various things to powers (braids, permutations, real numbers) and now having introduced these new mathematical "critters" called polynomials, one might naturally wonder what happens when we raise a polynomial to a power?
Recall that we can categorize polynomials by the number of terms they have (monomials have a single term, binomials have two, trinomials have three, etc). As such, we can ease into the question of powers of polynomials by considering each of these types of polynomials in sequence.
First, when it comes to finding a power of a monomial -- this is something with which we are already familiar. The rules of exponents governs what we need to do here. As an example, let us consider the monomial in two variables below that is being raised to the third power: $$(-2x^2y^5)^3 = (-2)^3 (x^2)^3 (y^5)^3 = -8x^6 y^{15}$$
However, powers of binomials are more interesting.
Limiting our discussion to integer exponents, we can of course find small powers of binomials by simply "doing the multiplication" (i.e., using the distributive property to expand the product into a polynomial). For example, consider the square of the binomial below: $$\begin{array}{rcl} (5x^3+3xy^2)^2 &=& (5x^3+3xy^2)(5x^3+3xy^2) \quad \quad {\tiny \textrm{first we distribute one factor to the terms of the other..}}\\ &=& 5x^3(5x^3+3xy^2) + 3xy^2(5x^3+3xy^2) \quad \quad {\tiny \textrm{then distribute again, twice}}\\ &=& 25x^6 + 15x^4y^2 + 15x^4y^2 + 9x^2y^4 \quad \quad {\tiny \textrm{there are some "like terms" we can collect -- in fact, they're identical!}}\\ &=& 25x^6 + 30x^4y^2 + 9x^2y^4 \end{array}$$
Cubing too, involves an exponent that is not so large that "doing the multiplication" via the distributive property is so tedius as to be off-putting. Consider the example that follows: $$\begin{array}{rcl} (4x^2 + 3)^3 &=& (4x^2 + 3)(4x^2 + 3)(4x^2 + 3)\\ &=& (4x^2(4x^2+3) + 3(4x^2+3))(4x^2+3)\\ &=& (16x^4 + 12x^2 + 12x^2 + 9)(4x^2+3)\\ &=& (16x^4 + 24x^2 + 9)(4x^2+3) \quad \quad {\tiny \textrm{Notice we again collect together two identical terms here, just like before (interesting!)}}\\ &=& 16x^4(4x^2+3) + 24x^2(4x^2+3) + 9(4x^2+3)\\ &=& 64x^6 + 48x^4 + 96x^4 + 72x^2 + 36x^2 + 27\\ &=& 64x^6 + 144x^4 + 108x^2 + 27 \end{array}$$ Alright, maybe that was a little worse than the square of a binomial we found just before. You might naturally worry that even higher powers of binomials are going to be even more tedious to expand into their polynomial forms via multiplication and the distributive property -- and you would be right! Wouldn't it be nice if there was a better/faster way to calculate such things?
Before getting to that, notice how in both of the above calculations there was a moment where we collected together two identical terms. Doesn't it strike you as odd that this happened? Maybe it was just a fluke. Try making up some other binomial and then squaring it. Oh my! You saw the same thing? Well that's interesting!
Of course, while seeing this happen every time we pick a binomial and square it makes one feel more comfortable believing it always happens -- doing so doesn't prove this must be the case. Perhaps we just didn't pick the right binomial. Maybe counter examples are rare and we just weren't lucky. Let's try this instead then -- suppose we simply let $a$ denote the first term of a binomial we wish to square and let $b$ denote the second term. So for example, in the square of the binomial below, $a = 7x^2y$ and $b = 4wp$: $$\require{color}(\underbrace{7x^2y}_{\color{red}{a}} + \underbrace{4wp}_{\color{red}{b}})^2$$
Then, we can write things in terms of $a$ and $b$, which makes our applications of the distributive properity simpler. The cost is that we have to substitute back in the expressions that $a$ and $b$ represent after expanding things, so that we see our original variables again: $$\begin{array}{rcl} (7x^2y + 4wp)^2 &=& (a+b)^2 \quad \quad {\tiny \textrm{presuming again that we defined $a = 7x^2y$ and $b= 4wp$}} \\ &=& (a+b)(a+b) \\ &=& a(a+b) + b(a+b) \\ &=& a^2 + ab + ba + b^2 \\ &=& a^2 + 2ab + b^2 \quad \quad {\tiny \textrm{of course $ab = ba$, which proves what we observed earlier always happens!}}\\ &=& (7x^2y)^2 + 2(7x^2y)(4wp) + (4wp)^2 \quad \quad {\tiny \textrm{here we have substituted back in $a=7x^2y$ and $b=4wp$}}\\ &=& 49x^4y^2 + 56x^2ywp + 16w^2p^2 \end{array}$$
As commented on above, the expansion of $(a+b)^2$ into $a^2 + 2ab + b^2$ proves that we always end up adding two identical terms when squaring a binomial (i.e., the terms given by $ab$ and $ba$), but it does more than that.
As $(a+b)^2 = a^2+2ab+b^2$ is always true, we can skip the details of this expansion and just use the $a^2+2ab+b^2$ form to expand squares of other binomials. For example: $$\begin{array}{rcl} (3xw^6 - 5q)^2 &=& (3xw^6 + (-5q))^2 \quad \quad {\tiny \textrm{$(a+b)^2$ is the square of a sum, so we write our square in this same form}} \\ &=& (3xw^6)^2 + 2(3xw^6)(-5q) + (-5q)^2 \quad \quad {\tiny \textrm{after expanding to $a^2 + 2ab + b^2$, where $a$ and $b$ are the 1st and 2nd terms above}}\\ &=& 9x^2w^{12} - 30xw^6q + 25q^2 \quad \quad {\tiny \textrm{after simplifying each term above}} \end{array}$$ As can be seen immediately upon comparing this last example and the expansion of the first square of a binomial we examined at the start of this section, using this "special product rule" to square binomials, $(a+b)^2 = a^2 + 2ab + b^2$ can clearly save us some work!
Of course, we can easily develop a special product rule to cube binomials too. All we really need to do is expand $(a+b)^3$: $$\begin{array}{rcl} (a+b)^3 &=& (a+b)(a+b)^2 \quad \quad {\tiny \textrm{splitting things in this way, we can take advantage of our new squaring rule!}}\\ &=& (a+b)(a^2 + 2ab + b^2) \\ &=& a(a^2 + 2ab + b^2) + b(a^2 + 2ab + b^2) \\ &=& a^3 + 2a^2b + ab^2 + ba^2 + 2ab^2 + b^3 \\ &=& a^3 + 3a^2b + 3ab^2 + b^3 \quad \quad {\tiny \textrm{after collecting like terms}} \end{array}$$
Having deduced that $(a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$, we can employ this special product rule to now find cubes of any binomial. As an example: $$\begin{array}{rcl} (4x - y^5)^3 &=& (4x + (-y^5))^3 \quad \quad {\tiny \textrm{$(a+b)^3$ is the cube of a sum, so we write things in that same form -- thus, here $a=4x$ and $b=-y^5$}}\\ &=& (4x)^3 + 3(4x)^2(-y^5) + 3(4x)(-y^5)^2 + (-y^5)^3 \quad \quad {\tiny \textrm{upon substituting $a=4x$ and $b=-y^5$ in $a^3 + 3a^2b + 3ab^2 + b^3$}}\\ &=& 64x^3 - 48x^2 y^5 + 12x y^{10} - y^{15} \end{array}$$
The above establishes two important "special product rules" for the expansion of squares and cubes of binomials. Namely, $$\boxed{\displaystyle{\begin{array}{rcl} (a+b)^2 &=& a^2 + 2ab + b^2\\ (a+b)^3 &=& a^3 + 3a^2b + 3ab^2 + b^3 \end{array}}}$$
We can find rules for higher powers of binomials through a similar process. Interestingly, a pattern seems to emerge when we do so. Consider the powers $(a+b)^n$ as $n$ takes on integer values from $0$ to $6$, inclusive: $$\begin{array}{c} (a+b)^0 = 1\\ (a+b)^1 = a + b\\ (a+b)^2 = a^2 + 2ab + b^2\\ (a+b)^3 = a^3 + 3a^2 b + 3ab^2 + b^3\\ (a+b)^4 = a^4 + 4a^3 b + 6a^2 b^2 + 4a b^3 + b^4\\ (a+b)^5 = a^5 + 5a^4 b + 10a^3 b^2 + 10a^2 b^3 + 5a b^4 + b^5\\ (a+b)^6 = a^6 + 6a^5 b + 15a^4 b^2 + 20a^3 b^3 + 15a^2 b^4 + 6a b^5 + b^6 \end{array}$$ For each such $n$, when we arrange the terms (as above) so that the exponents on $a$ descend from left to right, note that they do so by $1$ each time. As they do, the exponents on $b$ ascend by the same amount. In this way, the sum of the exponents on $a$ and $b$ remains $n$.
There is a pattern to the coefficients as well.
First notice that the first and last coefficients are always both equal to $1$. This should not be surprising, as when expanding $(a+b)^n$, there is only one way to generate the $a^n$ term -- by multiplying all the $b$ terms from each factor together. Similarly, there is only one way to generate the term with no $a$ factors (namely, $b^n$) -- by multiplying all the $b$ terms from each factor together.
Focusing on the rest of the coefficients, however, is where things get really intriguing!
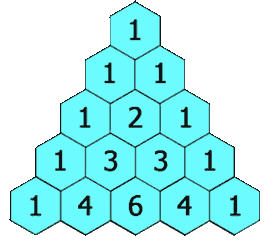
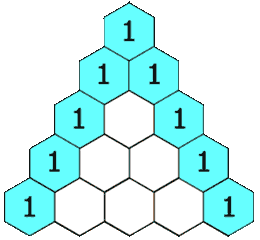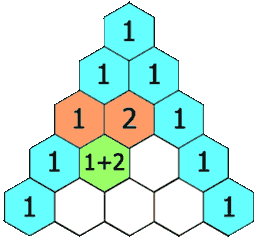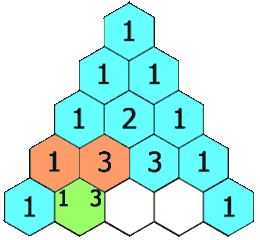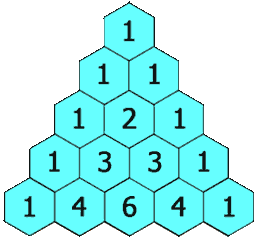
Suppose we write just the coefficients seen in $(a+b)^n$ in a triangular arrangement mirroring the calculations above. We do this below on the left. As the animated image on the right below suggests, each coefficient appears to be the sum of the two coefficients directly above.
We can easily prove this continues to be true for all subsequent rows corresponding to $n=5,6,7,\ldots$ using the principle of mathematical induction -- but instead of rigorously confirming this pattern in that way, perhaps the following observation will be sufficient to convince you it continues to hold for all positive integers $n$.
Consider powers of $(x+1)^n$ for $n=1,2,3,\ldots$ Treating the sum $(x+1)$ as the "base $x$" integer $(11)_x$, the value of $(x+1)^n$ becomes $11^n$, in base $x$. Of course, we know the following must be true in any base: $$\begin{array}{rcl} 11^0 &=& 1\\ 11^1 &=& 11\\ \end{array}$$ Notice the agreement of the digits of these with the coefficients seen in the expansions of $(a+b)^n$ for $n=1$ and $n=2$. Now consider $11^2$ in base $x$. $$\begin{array}{c@{\,},c@{\,},c@{\,},c@{\,},c@{\,}c} & & 1 & 1\\ & \times & 1 & 1\\\hline & & 1 & 1\\ & 1 & 1 & \\\hline & 1 & 2 & 1 \end{array} $$ As such, we can write $11^2$ in any base $x$ as $121$. Note how these digits correspond to the coefficients of $(a+b)^2 = a^2 + 2ab + b^2$. For still higher powers of $11$, we can use similar arithmetic to compute them. For example, we know $11^3 = 11^2 \times 11$, so we can find $11^3$ with: $$\begin{array}{c@{\,},c@{\,},c@{\,},c@{\,},c@{\,}c} & & 1 & 2 & 1\\ & \times & & 1 & 1\\\hline & & 1 & 2 & 1\\ & 1 & 2 & 1 & \\\hline & 1 & 3 & 3 & 1 \end{array} $$ Note how the digits of $11^3 = 1331$ match the coefficients seen in the expansion of $(a+b)^3$. Further, note where these digits came from -- by adding the digits $1\,2\,1$ to these same digits shifted one position to the left.
Similarly, we know $11^4 = 11^3 \times 11$, so we can compute $11^4$ with $$\begin{array}{c@{\,},c@{\,},c@{\,},c@{\,},c@{\,}c} & & 1 & 3 & 3 & 1\\ & \times & & & 1 & 1\\\hline & & 1 & 3 & 3 & 1\\ & 1 & 3 & 3 & 1 & \\\hline & 1 & 4 & 6 & 4 & 1 \end{array} $$ Here again, we have agreement between the digits of $11^4 = 14641$ and the coefficients in the expansion of $(a+b)^4$. These digits were found in a similar way, by adding the digits $1\,3\,3\,1$ to these same digits shifted one position to the left.
This pattern continues, although to find $11^5$ and beyond we will need to separate our "digits" with commas as each may actually require multiple digits to write (in the same way we encountered when subtracting polynomials treated as integers in some unknown base). Importantly, note how adding a sequence of numbers to itself, but shifted one position to the left, produces the same result as adding consecutive pairs of numbers in that sequence and appending to the left and right the first and last numbers of that sequence, respectively.
 |  |
 |
 |
The above is but one of many, many interesting patterns present in the "triangle of coefficients" described above, which is known as Pascal's Triangle. The triangle gets this particular name from the $17^{th}$ century mathematician and philosopher Blaise Pascal, who used it to solve probability problems and discovered and proved many interesting properties concerning it. That said, he was not the first person to study it. The Persian mathematician and engineer Al-Karaji, who lived from 935 to 1029 is currently credited with its discovery. (Interesting tidbit: Al-Karaji also introduced the powerful idea of arguing by mathematical induction.) Another Persian mathematician, Omar Khayyam popularized Al-Karaji's work to the point that even now in Iran, the triangle is often referred to as Khayyam's Triangle.
The triangle also showed up in China, well before Pascal worked with it. Chinese mathematicians Jia Xian and (later) Yang Hui also represented coefficients of binomial powers this way, and found interesting properties between the numbers contained in the triangle. In China, the triangle is called Yang Hui's triangle.
Even in Europe, there are multiple people associated with the triangle before Pascal. Notably, Petrus Apianus is responsible for the first printed record of the triangle when he used it as the frontispiece of a book in 1527. In Italy, the triangle is known as Tartaglia's triangle, named after the Italian algebraist Niccolo Tartaglia who published six rows of the triangle in 1556. (Interestingly, Tartaglia plays a prominent role in solving higher-order polynomial equations, on which we will focus considerable attention a bit later.) Gerolamo Cardano too (who also plays a significant role in our story to come), published the triangle and various ways of constructing it in 1570 -- again, well before Pascal.
As alluded to in its history, there are many patterns to the values in Pascal's triangle. One was mentioned above, whereby each row can be quickly constructed from the previous row. However, there is another, much more important (and provable) pattern that can be exploited to produce the numbers on any single row even faster, and without reference to any other rows. This elegant result, known as the Binomial Theorem then lets us expand $(x+y)^n$ for any non-negative integer $n$ as: $$(x+y)^n = x^n + {}_nC_1 x^{n-1} y + {}_nC_2 x^{n-2} y^2 + {}_nC_3 x^{n-3} y^3 + \cdots + {}_nC_{n-1} x y^{n-1} + y^n$$ Should the notation ${}_n C_k$ be unfamiliar (some texts denote this by ${n \choose k}$ instead), it calculates the number of combinations of $n$ things, taken $k$ at a time that one can form. That is to say, it counts the number of ways one can choose a set of $k$ objects when drawing from a group of $n$ objects. Students having seen some probability or statistics will likely know its value can be computed with the formula: $${}_n C_k = \frac{n!}{k!(n-k)!}$$ where $m!$, called the factorial of $m$ is defined by $m! = m \cdot (m-1) \cdot (m-2) \cdots 3 \cdot 2 \cdot 1$.
To see how these ideas are connected, consider the terms of the expansion of
$$(x+y)^n = \underbrace{(x+y)(x+y)(x+y) \cdots (x+y)}_{n \textrm{ factors}}$$Ultimately, each term of the expansion is formed by choosing either an $x$ or a $y$ from the first factor, and then choosing either an $x$ or a $y$ from the second factor, and then choosing an $x$ or a $y$ from the third factor, etc... up to finally choosing an $x$ or a $y$ from the $n^{th}$ factor, and then multiplying all of these together.
As such, each of these terms will consist of some number of $x$'s multiplied by some number of $y$'s, where the total number of $x$'s and $y$'s is $n$. For example, choosing $y$ from the first two factors, and $x$ from the rest will produce the term $x^{n-2}y^2$. Alternatively, choosing $x$ from the first $7$ factors and $y$ from the rest results in the term $x^7 y^{n-7}$.
Let's consider a specific example. Consider the terms we see from expanding the following expression (assuming we don't collect any "like terms" along the way):
$$\begin{array}{rcl} (x+y)^4 &=& (x+y)(x+y)(x^2 + xy + xy + y^2)\\\\ &=&(x+y)(x^3 + x^2y + x^2y + xy^2 + x^2y + xy^2 + y^3)\\\\ &=&x^4 + x^3y + x^3y + x^2y^2 +x^3y+x^2y^2 + xy^3 + x^3y + x^2 y^2 + x^2 y^2 + x y^3 + x y^3 + y^4 \end{array}$$Do you see how every term above takes the form $x^a y^b$ with $a+b=4$?
Now, when we finally "collect like terms", the resulting coefficient on $x^ay^b$ will be the number of times it appears in the expansion. As such, to figure out the coefficient on $x^ay^b$, we just need to figure out how many ways we can form a term that looks like $x^ay^b$.
Consider the terms $xy^3$ above. Note these terms were formed by letting three of the four $(x+y)$ factors contribute a $y$ to the product, with the remaining factor contributing an $x$. As such, the number of these terms will be given by the number of ways we can take $4$ factors and choose $3$ of them to contribute a $y$. In the parlance of the aforementioned combinations, this is given by ${}_4C_3$.
Likewise, the terms $x^2y^2$ were formed by letting $2$ of the $4$ factors contribute a $y$ to the product, with the remaining factors contributing a $x$. Consequently, the number of such terms will be equal to the number of ways we can can take $4$ factors and choose $2$ of them to contribute a $y$. Again, in terms of combinations, this is given by ${}_4C_2$.
In general, we can form terms of the form $x^{n-k}y^k$ by taking $n$ of our factors and choosing $k$ of them to contribute a $y$, which is given in the language of combinations by ${}_nC_k$.
Given that the non-collected terms of the expansion of $(x+y)^n$ can have as few as zero $y$'s or at most $n$ of them (with every integer possibility between), our possible terms are
$$x^n, \quad x^{n-1} y, \quad x^{n-2} y^2, \quad \ldots, \quad x y^{n-1}, \quad y^n$$Finally, noting that in the expansion of $(x+y)^n$, each $x^{n-k}y^k$ occurs ${}_nC_k$ times, we have: $$(x+y)^n = x^n + {}_nC_1 x^{n-1} y + {}_nC_2 x^{n-2} y^2 + {}_nC_3 x^{n-3} y^3 + \cdots + {}_nC_{n-1} x y^{n-1} + y^n$$ This result would be amazing enough -- but there is more! If we apply the formula for ${}_n C_k$ to compute ${}_n C_i$ and ${}_n C_{i+1}$, we will find they have all but two factors in common.
As such, we can generate each coefficient in the expansion of $(x+y)^n$ from the last.
Let us illustrate this by an example. Suppose we wish to generate the coefficients corresponding to the expansion of $(x+y)^6$. We know it must begin with a $1$, so we write that down.
$$1$$ Then, we multiply this value by the fraction $\frac{n}{1}$. The product gives the coefficient of the second term -- the one corresponding to $x^{n-1}y$. Since in this example, $n=6$, we have: $$1 \times \frac{6}{1} = 6$$ We create a new fraction by decreasing the numerator by 1 and increasing the denominator by 1. The product of this new fraction and our previous value gives the coefficient of the third term -- the one corresponding to $x^{n-2}y^2$. Here, we find this coefficient to be $$6 \times \frac{5}{2} = 15$$ Continuing in this way, decrementing the numerator, incrementing the denominator, and then multiplying the new fraction by the previous value (until we get a 1) yields the rest of the coefficients: $$\begin{array}{rcl} 15 \times \frac{4}{3} &=& 20\\ 20 \times \frac{3}{4} &=& 15\\ 15 \times \frac{2}{5} &=& 6\\ 6 \times \frac{1}{6} &=& 1\\ \end{array}$$ The sequence of coefficients so produced are: 1, 6, 15, 20, 15, 6, 1. This is, of course, the row of Pascal's triangle that provides the coefficients of $(x+y)^6 = x^6 + 6x^5y + 15x^4y^2 + 20x^3y^3 + 15x^2y^4 + 6xy^5 + y^6$, as seen in the version of the triangle below (one with more rows than previously shown):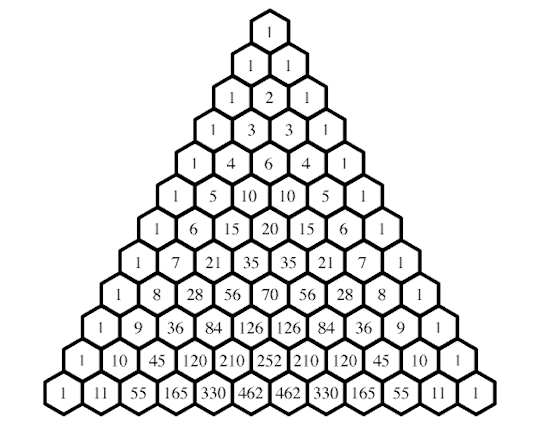
Consider the speed this last method offers for finding the numbers on the $n^{th}$ row of Pascal's triangle -- and consequently, the expansion of $(a+b)^n$. The following example illustrates things nicely:
Suppose we wanted to find $(2x+3w^2)^7$. First, we generate the coefficients we will need: $$1 \overset{\times \frac{7}{1}}{\longrightarrow} 7 \overset{\times \frac{6}{2}}{\longrightarrow} 21 \overset{\times \frac{5}{3}}{\longrightarrow} 35 \overset{\times \frac{4}{4}}{\longrightarrow} 35 \overset{\times \frac{3}{4}}{\longrightarrow} 21 \overset{\times \frac{2}{5}}{\longrightarrow} 7 \overset{\times \frac{1}{6}}{\longrightarrow} 1$$ This tells us that $$(a+b)^7 = a^7 + 7a^6 b + 21a^5 b^2 + 35 a^4 b^3 + 35 a^3 b^4 + 21 a^2 b^5 + 7 a b^6 + b^7$$ Then, we plug in $a=2x$ and $b=3w^2$ (from the first and second terms of the binomial we seek to square, respectively) and simplify: $$\begin{array}{c} (2x)^7 + 7(2x)^6(3w^2) + 21(2x)^5(3w^2)^2 + 35(2x)^4(3w^2)^3 + \cdots\\ \quad \quad \quad \quad 35 (2x)^3(3w^2)^4 + 21 (2x)^2(3w^2)^5 + 7(2x)(3w^2)^6 + (3w^2)^7\\ \end{array}$$ and then simplify each term to arrive at $$\begin{array} 128x^7 + 1344x^6w^2 + 6048x^5w^4 + 15120x^4 w^6 + 22680 x^3 w^8 + 20412 x^2 w^{10} + 10206 x w^{12} + 2187 w^{14} \end{array}$$
That's clearly a powerful theorem! (Spoiler alert -- we shall see that this just scratches the surface of what the Binomial Theorem can afford us. More on that later!)