Measuring Angles of Rotation in a Dimensionless Way

Recall that we have interpreted complex multiplication in the context of rotating points in a plane representing complex numbers about the origin. Such rotations may be some part of a full rotation, a full rotation or more, or even rotations in the opposite direction (when the associated angles are negative). Exactly how much we rotate has so far been described in terms of degrees.


Hipparchus of Rhodes
Most will be familiar with measuring angles in degrees, but what many may not know is that this unit of measurement traces back to the second century BC, when the Greek astronomer and mathematician Hipparchos of Rhodes began applying geometry to Babylonian astronomy (likely due to the amazing collection of astronomical data the Babylonians had compiled -- i.e., 800 years worth of nightly written records).

Despite the existence at the time of Euclid's Elements (c. 300 BC), a text which largely set the standard for learning geometry -- that work never provided a unit of measurement for angles besides the right angle. Hipparchos thus borrowed the Babylonian division of the ecliptic -- a great circle on the celestial sphere representing the sun's apparent path during the year, so called because lunar and solar eclipses can occur only when the moon crosses it.

The ancient Babylonians had divided this circular path into 12 sections called beru (interestingly, with names that in Greek translate to Gemini, Cancer, Leo, etc.). Then, they divided each of these sections into 30 equal subsections -- allowing the position of the sun to be described in one of $12 \cdot 30 = 360$ ways. Thus, the notion of a degree -- one $360^{th}$ of a full rotation -- was born. Why $12$ sections and $30$ subdivision you ask? Likely this was due to the fact that the calendar Babylonians used at the time was based on lunar cycles (cycles of the moon). Each such cycle lasted approximately 30 days (i.e., sometimes 29, othertimes 30), with $12$ lunar cycles occurring with each year.

All that fascinating history aside, there are better things we can use to compare the sizes of angles than the number of days in a lunar cycle!

As a starting place, consider the length of the path that some complex $z$ creates as it moves from $1$ counter-clockwise around the unit circle. Recall that one complete rotation about $0$ (the origin) should result in a path $2\pi$ times as long as the radius. But how long is that, actually -- are we measuring in inches? ..in feet?

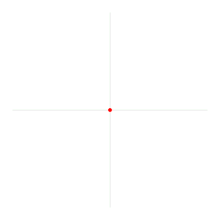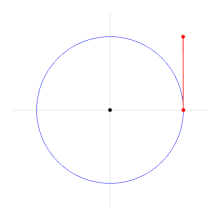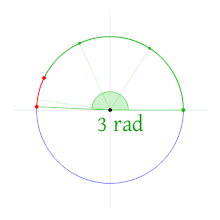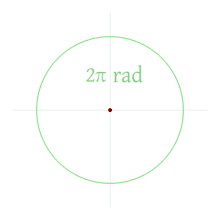Rather than try to pick some arbitrary dimension for the measure for these lengths (which is actually not unlike the somewhat arbitrary Babylonian division of a full rotation into 360 degrees), what if we instead define the angle measure by the ratio of the length of the path $z$ takes, and the length of the radius? Note that as both would presumably be measured in the same dimension, allowing these to cancel -- leaving a "dimensionless" radian measure of the angle in question.

For clarity (especially when using both degrees and radians), we sometimes write angles measures expressed in radians as $\theta$ rad, but given that radians are actually dimensionless, we will more often omit the "rad" part.

Measuring angles in this way equates a full rotation of $360^{\circ}$ to a radian measure of $2\pi$, and all other angles to their proportional equivalents (for example, half of $360^{\circ}$ is $180^{\circ}$ and half of $2\pi$ is $\pi$, so $180^{\circ}$ and $\pi$ are equal angle measures. Rotations of some common radian measures are shown below:


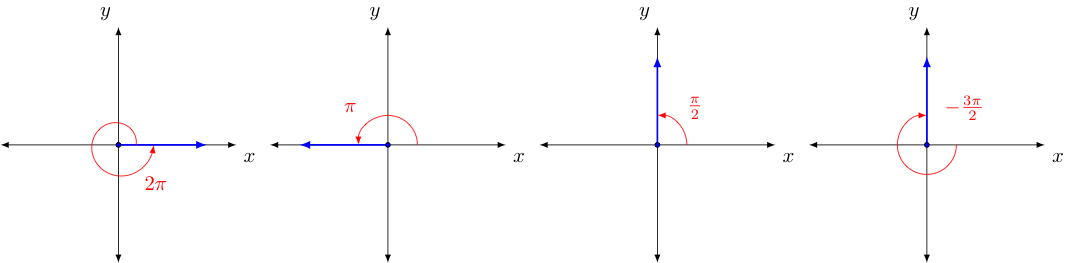
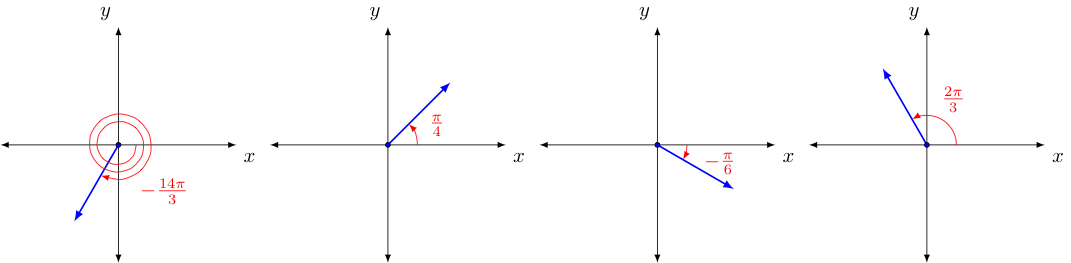
Given that a radian measure of $\pi$ is the same as $180^{\circ}$ and dividing both sides by $180$, we quickly see that $1^{\circ} = \frac{\pi}{180}$, we can then use this to easily convert the degree measure of any angle to radians and the radian measure of any angle to degrees. Some example conversions are shown below:

Precisely because they do not rely on any (arbitrarily) chosen dimension, the use of radians to measure angles will greatly simplify many things in both calculus and other areas of mathematics.