

 |  |
If we are to use a heap as a priority queue, then we need mechanisms for enqueueing (inserting) and dequeueing (removing) items from the collection. Let us consider the case of dequeueing first.
To keep things simple, let us assume the priority queue in question uses a max heap. As such, every parent must be greater than or equal to its children.
Consequently, the item with highest priority will thus be at index $1$ in the array. We have to keep the heap in the form of a complete binary tree, so upon removal of this element we'll have to replace it with something.
Of course, filling the hole made by our removal of the maximum element by moving another item in the heap to its location only serves to create a hole elsewhere -- except in one case. If we move the last element in the array (the right-most leaf in the deepest level of the tree), the tree is again made complete.
The only down side of doing this is that this item might be smaller than one or both of its children, in which case the heap order of the tree has been violated. Fortunately, we can restore the heap order through a process known as sinking the item. The short description of sinking is this: as long as the item has a greater child, we exchange it with its greatest child.
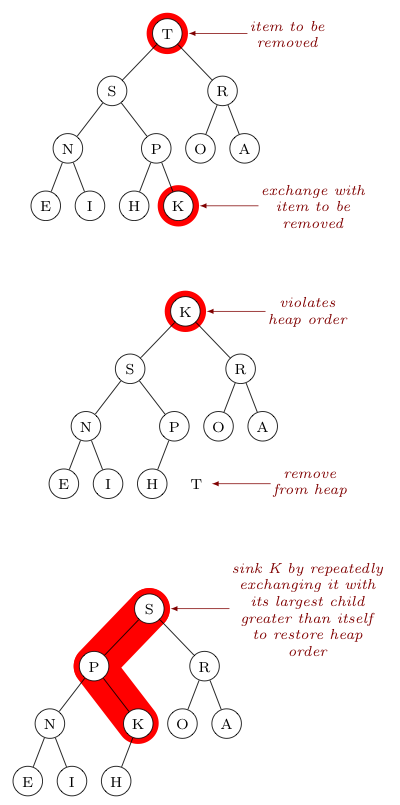
As a concrete example, consider the sequence of images shown below that describe the dequeuement of $T$ from a priority queue with the max heap representation given. The corresponding changes made in the associated array are shown on the right.
|
We start with the heap of $n=11$ elements described by the following array, $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11\\\hline - & T & S & R & N & P & O & A & E & I & H & K\\\hline \end{array}$$As our first step, we exchange the item at index $1$ (which has highest priority) with the item at index $n$. $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11\\\hline - & \color{red}{K} & S & R & N & P & O & A & E & I & H & \color{red}{T}\\\hline \end{array}$$We then remove the last element from the array. $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11\\\hline - & K & S & R & N & P & O & A & E & I & H & \color{gray}{-}\\\hline \end{array}$$Recalling that the children of the $k^{th}$ item in the array are at indices $2k$ and $(2k+1)$, we check to see if heap order has been violated by comparing the element $K$ at index $1$ with its children $S$ and $R$ at indices $2 \cdot 1 = 2$ and $2 \cdot 1 + 1 = 3$, respectively. Both children are larger, so it has indeed been violated. We thus exchange the item at index $1$ with the larger child at index $2$. $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11\\\hline - & \color{red}S & \color{red}K & R & N & P & O & A & E & I & H & \color{gray}{-}\\\hline \end{array}$$Again, $K$ (now at index $2$) has greater children ($N$ at index $2 \cdot 2 = 4$ and $P$ at index $2 \cdot 2 + 1 = 5$), so we exchange it with its greater child ($P$). $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11\\\hline - & S & \color{red}P & R & N & \color{red}K & O & A & E & I & H & \color{gray}{-}\\\hline \end{array}$$Seeing $K \gt H$, its only child, we know heap order has now been restored. The priority queue is now ready for either the removal of its next highest priority item or the insertion of a new item. |
Below is a partial implementation of a max heap that can serve as a priority queue, focusing on the removal of the maximum item in the heap (i.e. the highest priority item):
public class MaxHeap<Item extends Comparable<Item>> {
private Item[] items; // the array in which the items of the heap are stored
private int size; // keeps track of the number of items stored in the heap
public MaxHeap(int capacity) {
items = (Item[]) (new Comparable[capacity+1]); // remember, generic array
// creation is not allowed.
// also, we use a capacity here
// for simplicity, but having a
// no-arg constructor and using
// resizing arrays would be better.
size = 0; // superfluous, of course
}
private boolean less(int v, int w) { // helper method to compare items to one another
return (items[v]).compareTo(items[w]) < 0;
}
private void exch(int i, int j) { // helper method to exchange items at indices i and j
Item tmp = items[i];
items[i] = items[j];
items[j] = tmp;
}
...
public Item removeMaxItem() { // dequeues the highest priority item
Item highestPriorityItem = items[1];
items[1] = items[size]; // moves the last element to the top of the heap
items[size] = null; // to prevent loitering
size--; // update the size instance variable
sink(1); // when heap order is violated, this will fix it
return highestPriorityItem;
}
private void sink(int k) {
// while k is smaller than either (or both) of the existing children,
// exchange with the greater child (so heap order is preserved)
while (2*k <= size) { // terminate when doubling to find the next child
// fails due to being outside the array
// (i.e., results in an index bigger than size)
int j = 2*k; // start with left child (for now)
// if right child exists and is larger, we will update this choice
// remember, if an exchange happens, then one of the children
// becomes the parent of the other. to preserve heap order
// we need the greater child promoted to parent.
if ((j < size) && less(j,j+1))
j++;
if (less(j,k)) // k is greater than its children - stop sinking
break;
exch(k,j); // swap child and parent k
k = j; // update position of this sinking parent,
}
}
}
The implementation of a min heap would be similar, except in that case we sink an item when it is greater than either (or both) of its children.
Note that because the element to be removed could be compared with up to two children per level, the worst case comparison cost for removing an item from a heap-implemented priority queue is $\sim 2\log_2 n$.
Of course, we won't be able to use the above code to remove things from a max heap implemented priority queue if we can't first add things to it! The process for inserting an item associated with a given key is similar to removal, except reversed in a certain sense.
During insertion, while we don't have a "hole" in the array to fill, we must still be mindful about where we insert the new element. We can initially insert the element in question to the immediate right of the right-most leaf (unless the level is full, in which case we insert the element as the left-most leaf in a new level). This keeps the underlying tree complete.
However, as with the initial exchange during removal of items, the insertion just made may violate heap order if we have created a new leaf that is greater than its parent.
Just as before, we can restore heap order, although this time the process to fix things is known as swimming the item upwards. Specifically, as long as the parent of our inserted item is smaller than the inserted item, we exchange these two items.
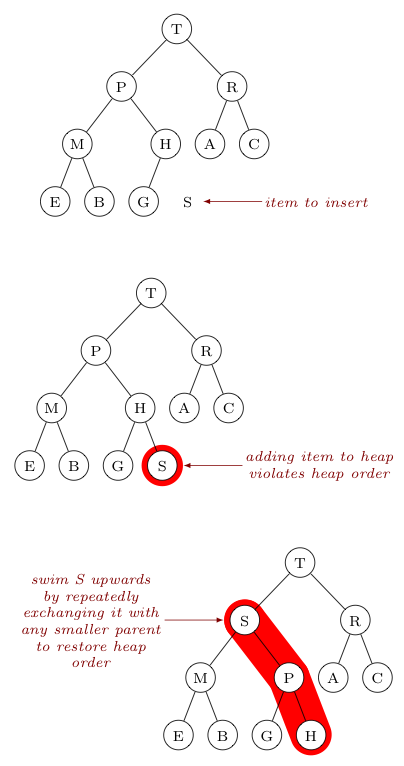
Again let us consider a more concrete example in the images below which show the insertion (enqueuement) of an item with key $S$ in a priority queue with the the max heap representation given. Again, the corresponding array operations are shown on the right.
|
We start with the heap of $n=10$ elements described by the following array, $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11\\\hline - & T & P & R & M & H & A & C & E & B & G & -\\\hline \end{array}$$As our first step, we add the new item $S$ at index $(n+1)$, just after the right-most existing element in the array. $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11\\\hline - & T & P & R & M & H & A & C & E & B & G & \color{red}S\\\hline \end{array}$$Recalling that the parent of the item at index $k$ is at position $\lfloor k/2 \rfloor$, we check to see if heap order has been violated by comparing the element $S$ at index $11$ with its parent $H$ at index $\lfloor 11/2 \rfloor = 5$. This parent is smaller than $S$, so heap order has indeed been violated. We thus exchange these two items. $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11\\\hline - & T & P & R & M & \color{red}S & A & C & E & B & G & \color{red}H\\\hline \end{array}$$Again, the parent $P$ (at index $\lfloor 2 \rfloor$) of $S$ (now at index $5$) is smaller than $S$, so we similarly exchange these two items in the array. $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11\\\hline - & T & \color{red}S & R & M & \color{red}P & A & C & E & B & G & H\\\hline \end{array}$$Seeing $T \gt S$, we know heap order has now been restored. The priority queue is now ready for additional insertions or the removal of its highest priority item. |
In the code below, we have an implementation of instance methods insert(Item item) and swim(int k) for the MaxHeap class started above, using the method of insertion just described.
public void insert(Item item) {
items[size+1] = item; // add the new item to the array
size++; // update the size instance variable
swim(size); // when heap order is violated, this will fix it
}
private void swim(int k) {
while ((k > 1) && less(k/2,k)) { // while k is not root and greater than parent,
exch(k/2,k); // exchange it with its parent
k = k/2;
}
}
Note that the comparison cost of inserting items in this way into a heap-implemented priority queue is $O(\log_2 n)$.