

 |  |
With a conceptual understanding of 2-3 trees under our belt, the natural question to next ask is "How do we implement a 2-3 tree?"
One could try to keep up with three different node classes -- one for 2-nodes, another for 3-nodes, and a final one for the temporary 4-nodes. This however, is fraught with complications. For starters, how do we accomplish transforming one type node into another during the insertion process? Clearly this is more challenging than a simple cast. For example, the underlying comparisons being done to navigate the tree during a search or insertion are decidedly different. Further, adding a key -- and dealing with all of the cases that result from doing that in the correct order -- makes turning a 2-node into a 3-node, or turning a 3-node temporarily into a 4-node, tricky indeed. Finally, remember that as we move up the tree during an insertion, we must split 4-nodes into multiple 2-nodes. Sometimes this involves passing information to the parent nodes, while other times it requires a new root node be formed -- which complicates things even further.
Granted, tackling a direct implementation of a 2-3 tree is not impossible. It can be done with some effort and care to attend to all of the cases that result. However, there is a much simpler way -- one that requires we define only a single node class. The trick is to add a "bit of color" to our nodes...
Consider the following 2-3 tree, where the 3-nodes are drawn with dashed ellipses and red dashes between their respective keys. Importantly, at this point we haven't changed anything structurally about the 2-3 tree. We are just drawing its 3-nodes a little differently.

Now compare the above picture to the following binary tree, where some of the links are drawn in red. Around these red links and the nodes they connect we draw dashed ellipses to highlight how these links pair up perfectly with the 3-nodes in the previous picture.
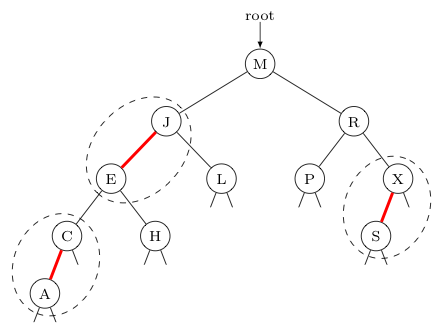
Amazingly, by turning each 3-node into a pair of 2-nodes with a red link between them, we have replicated -- in a reversable way -- the structure of a 2-3 tree in a form more like that of a binary search tree!
As some consistency will greatly reduce the number of cases to consider in future manipulations of such trees, we adopt the convention that the greater key of each 3-node will always be turned into the "parent" of the lesser key of that node. This has the effect of making all of the ellipses "droop" on their left side. This in turn tends to make the left sides of such trees (and their subtrees) appear slightly deeper than their right sides. As such, the resulting trees are described as left-leaning red-black trees
Our choice to make the greater keys the parents is completely arbitrary, of course -- had we instead insisted the lesser key always be the parent, then the resulting red links would have "drooped right", making the right side appear to be slightly deeper. If this choice is made, we call the trees that result right-leaning red-black trees.
Importantly, the conversion of 3-nodes to these left-leaning red-linked pairs of 2-nodes preserves the symmetric order of the tree. To convince yourself of this, think about how the subtrees below a given 3-node move under this transformation. As an example, consider the following:
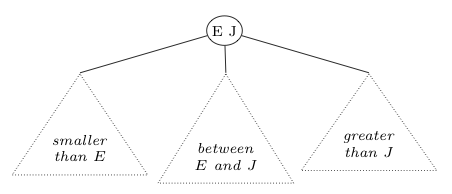 |
 |
Of course, 2-3 trees must not only be in symmetric order -- they must also be perfectly balanced.
Recall perfect balance means that every path from the root to a leaf has the same length. If we count both the red and black links in a red-black tree, it would appear our red-black trees are not perfectly balanced.
However, the red links should really just be thought of the "glue" that binds two keys together into a 3-node. In the underlying 2-3 tree, they don't add anything to the path length.
In a red-black tree, we focus only on the remaining black links. In a given red-black tree, if one draws any path from the root to a leaf and counts only the black links on that path, the result will be the same. We refer to this as perfect black balance.
For a binary tree with red and black links to represent a 2-3 tree, however, symmetric order and perfect black balance are not enough. Recall 3-nodes have 2 keys and 2-nodes have only 1 key. As such, we must limit the number of keys that are "glued together" via the red links to two or less. This means that no node can be connected to more than one red link.