

 |  |
Below is a method which uses a stack of integers with typical push and pop operations:
public static int foo(int x, int y) {
if (x <= 0 || y <= 0)
return 0;
stack.push(y);
return foo(x - 1, y-1) + stack.pop();
}
Assuming the stack is initially empty, draw a snapshot of the stack after every push and pop statement for each recursive call for foo(3,4). Label each stack snapshot with the recursive call, and the push or pop statement. For example, the following shows the first two snapshots of the stack after the push statement for the call foo(3,4) and after the push statement for the call foo(2,3).
4 --- foo(3,4) - push 3 4 --- foo(2,3) - push
To what integer value does foo(3,4) evaluate when invoked?
2
3 3 3
4 4 4 4 4
======== ======== ======== ======= ======= =======
foo(3,4) foo(2,3) foo(1,2) pop pop pop
push push push
foo(3,4) = foo(2,3) + pop
foo(2,3) = foo(1,2) + pop
foo(1,2) = foo(0,1) + pop
foo(0,1) = 0
So,
foo(1,2) = 0 + 2 = 2
foo(2,3) = 2 + 3 = 5
foo(3,4) = 5 + 4 = 9 <-- final answer = 9
In using the shunting yard algorithm to convert A - (B ^ C ^ D * E) + F / G from partially parenthesized infix form to postfix form, list the elements that are popped from the operator stack in the order they are popped.
^ ^ * ( - / +
Write a class ShuntingYard that prompts the user to enter an expression in infix form (possibly only partially parenthesized), and then prints an equivalent expression in fully parenthesized postfix form -- where operators come after their operands.
You may assume that the user input will separate operands, operators, and parentheses with spaces, and the operators include only "+", "-", "*", "/", and "^".
$ java ShuntingYard↵ Enter an infix expression to convert to postfix form: ( A ^ B ^ C * ( D - E ) )↵ A B C ^ ^ D E - *
Expand the class ShuntingYard by adding a method named toPreFix(String s) and changing the main(String[] args) method so that it prompts the user to enter an expression in infix form (possibly only partially parenthesized), and then prints an equivalent expression in fully parenthesized prefix form -- where operators come before their operands, and every operator and its operands appear in parentheses. A sample run is shown below.
You may assume that the user input will separate operand and operator tokens with spaces, and the operators include only "+", "-", "*", "/", and "^".
$ java ShuntingYard↵ Enter an infix expression to convert to prefix form: A + B * C ^ D - E↵ ( - ( + A ( * B ( ^ C D ) ) ) E )
One can solve the N-Queens problem by implementing a backtracking algorithm using a stack. Show the values of such a stack after each push or pop operation for 4-Queens problem until the first solution is found. You may assume the rows and columns are both indexed from $0$ to $3$ (bottom-to-top and left-to-right, as appropriate) and that lower indexed rows are tried before higher ones, and the same is true for columns.
2
1 0 0
2 3 3 3 3 3 3
0 0 0 0 0 0 0 1 1 1 1
=== === === === === === === === === === === ===
Complete the implementation of the class NQueensSolver meant to prompt the user for a board size, and then find and print all solutions to the NQueens problem (i.e., placing $n$ queens on an $n \times n$ board so that no queen can attack any other) for that size board, as the sample run below suggests.
Note the template file uses the StateAllowingBacktracking interace, which should be kept intact
Hint: an $8 \times 8$ board has 92 solutions.
$ java NQueens↵ Enter board size to solve: 4↵ * Q * * * * * Q Q * * * * * Q * * * Q * Q * * * * * * Q * Q * * Solutions Found: 2
In a Sudoku puzzle, one is given a partially filled $9 \times 9$ grid. The goal is to assign digits (from 1 to 9) to the empty cells so that every row, column, and $3 \times 3$ subgrid contains exactly one instance of the digits from 1 to 9.
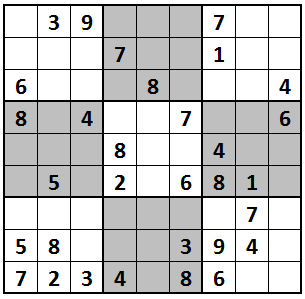
Complete the implementation of the class SudokuSolver whose constructor accepts a 2d-array of ints representing a sudoku puzzle (where entries of $0$ in the array signify empty cells). The provided main() method finds and prints the solution (if it exists) to two puzzles specified in this way, as the sample run below suggests.
Importantly, the partial implementation provided references the interface StateAllowingBacktracking. Make sure you understand how this impacts the code you must write.
Note, the colored text in the output may or may not be supported by your terminal, depending on your platform (e.g., macOS, windows, various flavors of linux/unix). If your platform does not support color, see the relevant comment in the template file SudokuSolver.
$ java SudokuSolver↵ NEW PUZZLE: ·39┃···┃7·· ···┃7··┃1·· 6··┃·8·┃··4 ━━━╋━━━╋━━━ 8·4┃··7┃··6 ···┃8··┃4·· ·5·┃2·6┃81· ━━━╋━━━╋━━━ ···┃···┃·7· 58·┃··3┃94· 723┃4·8┃6·· 1 solutions(s) found: 139┃624┃785 248┃759┃163 675┃381┃294 ━━━╋━━━╋━━━ 814┃937┃526 962┃815┃437 357┃246┃819 ━━━╋━━━╋━━━ 491┃562┃378 586┃173┃942 723┃498┃651 ----------------- NEW PUZZLE: 316┃578┃42· 52·┃···┃··· ·87┃···┃·31 ━━━╋━━━╋━━━ ··3┃·1·┃·8· 9··┃863┃··5 ·5·┃·9·┃6·· ━━━╋━━━╋━━━ 13·┃···┃25· ···┃···┃·74 ··5┃2·6┃3·· 0 solutions(s) found:
Suppose we wish to form a line of $k$ things by selecting these $k$ things from a (possibly longer) line of $n$ things and putting them in some (possibly different) order. This is called a "permutation of $k$ things selected from $n$ things".
To make this idea more concrete, suppose we are interested in selecting $k=4$ people from a longer line of $n=6$ people: Alice, Bob, Carl, Doug, Edgar, and Frank, respectively. One way we could do this would be to form the line (starting with Carl): Carl, Edgar, Alice, Frank.
For those that have had probability or statistics, this may look familiar. In that context, we often want to know how many ways this could be done, calling the result the number of "permutations of $n$ things, taken $k$ at a time".
Granted, for this problem we will be more worried about precisely how things are getting rearranged for individual permutations than we will be about counting how many possible rearrangements exist.
Note that we can describe exactly "what moves where" in a given permutation of this form with just a single $k$-tuple, like $(3,5,1,6)$. Indeed, this particular $4$-tuple actually describes the exact same permutation as the one described using people above -- it just leaves out what the "things" are, focusing instead on their positions.
In this particular case, one will want to think of $(3,5,1,6)$ as "the rearrangement that moves the $3^{rd}$ thing to the first position, the $5^{th}$ thing to the second position, the $1^{st}$ thing to the third position, and the $6^{th}$ thing to the fourth and final position. Permutations described with different numbers (or numbers of numbers) can be interpreted in a similar manner.
If the $n$ things are all distinct, note that one will never see a number appear more than once in the same permutation, when written in this $k$-tuple format. Use this fact to complete the class PermutationsFinder so that for given positive integers $n$ and $k$ (with $n \ge k$) supplied by the user, it shows all of the ways one could permute $k$ things taken from a group of $n$, followed by an overall count of those possible permutations.
Note, the template file references the StateAllowingBacktracking interface, which should be kept intact.
A sample run is shown below
$ java PermutationsFinder↵ Enter n and k separated by a space to find all permutations of k values selected from 1 to n: 5 3↵ (1,2,3) (1,2,4) (1,2,5) (1,3,2) (1,3,4) (1,3,5) (1,4,2) (1,4,3) (1,4,5) (1,5,2) (1,5,3) (1,5,4) (2,1,3) (2,1,4) (2,1,5) (2,3,1) (2,3,4) (2,3,5) (2,4,1) (2,4,3) (2,4,5) (2,5,1) (2,5,3) (2,5,4) (3,1,2) (3,1,4) (3,1,5) ... (5,4,2) (5,4,3) number of permutations found: 60
Suppose we wish to list all the ways of simply selecting $k$ things from a group of $n$ (where order in which they are selected does not matter at all). As with permutations, this idea will be familiar to those who have taken probability or statistics. In those courses, we count how many ways this can be done, calling the result the "combinations of $n$ things taken $k$ at a time", or sometimes using the more elliptical phrase "$n$ choose $k$".
We can describe the individual combinations in a couple of ways. One way would be to simply list the elements of the subset selected. So for $n=5$ elements: $\{1,2,3,4,5\}$, perhaps we choose $k=3$ of them by picking the subset $\{2,4,5\}$. Another way to describe the same selction is to list all $n$ elements and mark which are to be included and which are to be omitted from our resulting subset. If we use an "I" to indicate inclusion and "O" to indicate omission, we can see that the sequence $\{O,I,O,I,I\}$ will correspond to that same subset $\{2,4,5\}$, presuming the element included or omitted corresponds to the position in the sequence for the "I" or "O".
With all this in mind, complete the class CombinationsFinder so that for given positive integers $n$ and $k$ (with $n \ge k)$ supplied by the user, it shows all of the possible combinations of $k$ numbers taken from the $n$ numbers $1,2,3,\ldots,n$ using both of the aforementioned ways to describe those combinations, followed by a count of how many were found.
Note, the template file references the StateAllowingBacktracking interface, which should be kept intact.
A sample run is shown below
$ java CombinationsFinder↵ Enter n and k separated by a space to find all combinations of k values selected from 1 to n: 5 3↵ {IIIOO} = {1,2,3} {IIOIO} = {1,2,4} {IIOOI} = {1,2,5} {IOIIO} = {1,3,4} {IOIOI} = {1,3,5} {IOOII} = {1,4,5} {OIIIO} = {2,3,4} {OIIOI} = {2,3,5} {OIOII} = {2,4,5} {OOIII} = {3,4,5} number of combinations found: 10
In the game of chess, a knight is a piece often shaped in the form of a horse's head and neck, that in one move can travel to any other space on the board that is either up/down 2 spaces and left/right 1 space from its current location, or left/right 2 spaces then up/down 1 space from its current location. In the course of doing so, knights may "jump" over any other pieces in their paths. This means that a knight may move in up to 8 different ways from a given square it occupies, as shown below.
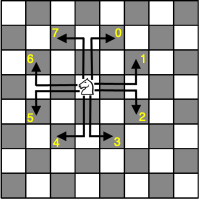
A knight's tour is a sequence of moves of a knight on a chessboard whereby the knight visits every square exactly once.
Complete the class KnightsTourSolver (which depends on the StateAllowingBacktracking interface) that imagines a $n \times n$ chessboard as an array and finds all knight's tours of that board starting with the position in the upper left corner, which is presumed to be the position in row $0$ and column $0$ of the corresponding array.
Legal moves are explored in the order enumerated in the image above. Solutions found should be numbered and displayed as two-dimensional arrays showing the order in which each cell is visited, in a manner consistent with the portion of the sample run shown below.
$ java KnightsTourSolver↵ Enter board size to solve: 5 Solution 1 1 20 17 12 3 16 11 2 7 18 21 24 19 4 13 10 15 6 23 8 25 22 9 14 5 Solution 2 1 18 23 12 3 16 11 2 7 22 19 24 17 4 13 10 15 6 21 8 25 20 9 14 5 Solution 3 1 10 15 20 3 16 21 2 7 14 11 24 9 4 19 22 17 6 13 8 25 12 23 18 5 ... Solution 304 1 10 15 20 23 16 5 22 9 14 11 2 19 24 21 6 17 4 13 8 3 12 7 18 25
In an $n \times n$ Latin Square, filled with $n$ different symbols, each symbol occurs exactly once in each row and exactly once in each column. For example, the following is a Latin Square where $n=3$:
$$\begin{array}{|c|c|c|}\hline 1 & 2 & 3\\\hline 3 & 1 & 2\\\hline 2 & 3 & 1\\\hline \end{array}$$ Complete the classLatinSquareFinder (which depends on the StateAllowingBacktracking interface) that prompts the user for the value of $n$ (you may assume $2 \le n \le 9$) and then finds all Latin Squares using symbols $1$ to $n$ on an $n \times n$ board, displays them, and reports how many there are.
Below is a sample run:
$ java LatinSquares↵ Enter n: 4↵ Solutions: 1234 2143 3412 4321 1234 2143 3421 4312 . . . 4321 3412 2143 1234 576 solutions found!
Create a class MazeSolver, whose constructor accepts a 2d-array of int values representing a maze (entries of $1$ correspond to walls and entries of $0$ correspond to empty corridors), with the starting position for the maze in first row and second column, and the finishing position in the bottom row and second-to-last column. A sample run where one finds and prints -- for 3 separate mazes -- how many solutions exist and the solution path for each is given below.
$ java MazeSolver↵
NEW MAZE:
░S░░░░░░░░░
░ ░ ░░ ░
░ ░░ ░ ░ ░
░ ░ ░░ ░
░ ░░ ░ ░
░░░ ░ ░ ░░
░ ░░ ░ ░
░ ░ ░ ░ ░
░░░░░░░░░F░
1 solutions(s) found:
░S░░░░░░░░░
░•░ ░░•••░
░•░░ ░••░•░
░•░••••░░•░
░•••░░ ░••░
░░░ ░ ░•░░
░ ░░ ░••░
░ ░ ░ ░•░
░░░░░░░░░F░
NEW MAZE:
░S░░░░░░░░░░░░░░░░░░░
░ ░ ░ ░ ░
░░░ ░░░ ░ ░░░ ░░░░░ ░
░ ░ ░ ░ ░ ░ ░
░ ░░░ ░░░ ░ ░ ░░░ ░ ░
░ ░ ░ ░
░ ░░░░░░░ ░░░░░░░ ░ ░
░ ░ ░ ░ ░ ░ ░
░ ░ ░ ░░░░░░░ ░░░ ░ ░
░ ░ ░ ░ ░ ░
░░░ ░ ░░░░░░░ ░░░░░ ░
░ ░ ░ ░ ░ ░
░ ░░░ ░ ░ ░ ░ ░░░░░ ░
░ ░ ░ ░ ░ ░ ░ ░
░ ░ ░ ░ ░ ░░░░░ ░ ░ ░
░ ░ ░ ░ ░ ░ ░ ░
░ ░░░ ░ ░░░░░ ░ ░░░ ░
░ ░ ░ ░ ░ ░ ░
░ ░░░░░ ░ ░░░ ░░░ ░ ░
░ ░ ░ ░
░░░░░░░░░░░░░░░░░░░F░
4 solutions(s) found:
░S░░░░░░░░░░░░░░░░░░░
░•••••••░ ░ ░ ░
░░░ ░░░•░ ░░░ ░░░░░ ░
░ ░•••░ ░ ░•••••░ ░
░ ░░░•░░░ ░ ░•░░░•░ ░
░ ••••••••• ░•░ ░
░ ░░░░░░░ ░░░░░░░•░ ░
░ ░ ░ ░ ░ •••••░ ░
░ ░ ░ ░░░░░░░•░░░ ░ ░
░ ░ ░•░ ░ ░
░░░ ░ ░░░░░░░•░░░░░ ░
░ ░ ░ ░ • ░ ░
░ ░░░ ░ ░ ░ ░•░░░░░ ░
░ ░ ░ ░ ░ ░•••••░ ░
░ ░ ░ ░ ░ ░░░░░ ░•░ ░
░ ░ ░ ░ ░ ░ ░•••░
░ ░░░ ░ ░░░░░ ░ ░░░•░
░ ░ ░ ░ ░ ░•░
░ ░░░░░ ░ ░░░ ░░░ ░•░
░ ░ ░ •░
░░░░░░░░░░░░░░░░░░░F░
░S░░░░░░░░░░░░░░░░░░░
░•••••••░ ░ ░ ░
░░░ ░░░•░ ░░░ ░░░░░ ░
░ ░•••░ ░ ░ ░ ░
░ ░░░•░░░ ░ ░ ░░░ ░ ░
░••••• ░ ░ ░
░•░░░░░░░ ░░░░░░░ ░ ░
░•░ ░ ░ ░ ░ ░
░•░ ░ ░░░░░░░ ░░░ ░ ░
░•••░ ░ ░ ░ ░
░░░•░ ░░░░░░░ ░░░░░ ░
░ •••░ ░ ░ ░ ░
░ ░░░•░ ░ ░ ░ ░░░░░ ░
░ ░•░ ░ ░ ░ •••░ ░
░ ░ ░•░ ░ ░░░░░•░•░ ░
░ ░ ░•░ ░ ░•░•••░
░ ░░░•░ ░░░░░ ░•░░░•░
░ ░•••░ ░•••░ ░•░
░ ░░░░░•░ ░░░•░░░ ░•░
░ ░ •••••••░ •░
░░░░░░░░░░░░░░░░░░░F░
░S░░░░░░░░░░░░░░░░░░░
░••• ░ ░ ░ ░
░░░•░░░ ░ ░░░ ░░░░░ ░
░•••░ ░ ░ ░•••••░ ░
░•░░░ ░░░ ░ ░•░░░•░ ░
░••••••••••••• ░•░ ░
░ ░░░░░░░ ░░░░░░░•░ ░
░ ░ ░ ░ ░ •••••░ ░
░ ░ ░ ░░░░░░░•░░░ ░ ░
░ ░ ░•░ ░ ░
░░░ ░ ░░░░░░░•░░░░░ ░
░ ░ ░ ░ • ░ ░
░ ░░░ ░ ░ ░ ░•░░░░░ ░
░ ░ ░ ░ ░ ░•••••░ ░
░ ░ ░ ░ ░ ░░░░░ ░•░ ░
░ ░ ░ ░ ░ ░ ░•••░
░ ░░░ ░ ░░░░░ ░ ░░░•░
░ ░ ░ ░ ░ ░•░
░ ░░░░░ ░ ░░░ ░░░ ░•░
░ ░ ░ •░
░░░░░░░░░░░░░░░░░░░F░
░S░░░░░░░░░░░░░░░░░░░
░••• ░ ░ ░ ░
░░░•░░░ ░ ░░░ ░░░░░ ░
░•••░ ░ ░ ░ ░ ░
░•░░░ ░░░ ░ ░ ░░░ ░ ░
░• ░ ░ ░
░•░░░░░░░ ░░░░░░░ ░ ░
░•░ ░ ░ ░ ░ ░
░•░ ░ ░░░░░░░ ░░░ ░ ░
░•••░ ░ ░ ░ ░
░░░•░ ░░░░░░░ ░░░░░ ░
░ •••░ ░ ░ ░ ░
░ ░░░•░ ░ ░ ░ ░░░░░ ░
░ ░•░ ░ ░ ░ •••░ ░
░ ░ ░•░ ░ ░░░░░•░•░ ░
░ ░ ░•░ ░ ░•░•••░
░ ░░░•░ ░░░░░ ░•░░░•░
░ ░•••░ ░•••░ ░•░
░ ░░░░░•░ ░░░•░░░ ░•░
░ ░ •••••••░ •░
░░░░░░░░░░░░░░░░░░░F░
NEW MAZE:
░S░░░░░░░░░░░░░░░░░░░
░ ░ ░ ░ ░ ░
░ ░ ░░░ ░ ░ ░░░ ░ ░ ░
░ ░ ░ ░ ░ ░ ░ ░
░ ░ ░ ░ ░░░ ░ ░░░░░░░
░ ░ ░ ░ ░ ░ ░
░ ░░░ ░ ░ ░░░░░ ░░░ ░
░ ░ ░ ░ ░
░ ░░░ ░ ░░░ ░░░░░░░ ░
░ ░ ░ ░ ░ ░ ░
░ ░ ░░░░░ ░░░░░░░ ░░░
░ ░ ░ ░ ░ ░ ░
░ ░ ░░░░░ ░ ░ ░ ░░░ ░
░ ░ ░ ░ ░ ░
░ ░ ░░░░░ ░░░ ░ ░ ░ ░
░ ░ ░ ░ ░ ░ ░
░ ░░░ ░░░░░ ░ ░ ░ ░ ░
░ ░ ░ ░ ░ ░ ░ ░
░ ░░░░░ ░░░ ░░░ ░ ░░░
░ ░ ░ ░ ░ ░
░░░░░░░░░░░░░░░░░░░F░
0 solutions(s) found: