

 |  |
 A priority queue is an abstract data type similar to a queue in that it can serve as a "holding area" for data or objects before they are processed in some way. However, unlike a queue where items are processed in the same order in which they were enqueued, in a priority queue each item has some associated priority level, and items are processed in order of priority. As a (somewhat somber) real world example, one sees this type of organization in the process of medical triage following some natural disaster or other mass casualty/fatality event. In these situations, patients are not treated in the order they arrive at the hospital, but rather in an order based on the severity of their condition. Each patient is given some tag or wristband like those shown at right to indicate their priority level, so that medical practitioners know who to treat next.
A priority queue is an abstract data type similar to a queue in that it can serve as a "holding area" for data or objects before they are processed in some way. However, unlike a queue where items are processed in the same order in which they were enqueued, in a priority queue each item has some associated priority level, and items are processed in order of priority. As a (somewhat somber) real world example, one sees this type of organization in the process of medical triage following some natural disaster or other mass casualty/fatality event. In these situations, patients are not treated in the order they arrive at the hospital, but rather in an order based on the severity of their condition. Each patient is given some tag or wristband like those shown at right to indicate their priority level, so that medical practitioners know who to treat next.
One place where a priority queue is often needed is in the process manager of an operating system. Lots of tasks/users are vying for limited resources. How should the operating system choose which task should be executed next? FIFO is a possibility - but not the most practical. One long task could prevent many short (but potentially important) ones from being accomplished. By assigning priorities to the tasks and using a priority queue, time can be used more wisely and disgruntled users can be kept at a minimum.
Priority queues are used in a host of other applications as well: web caching, spam filtering, data compression, path finding, etc. They can even be used to sort data.
The implementation of a priority queue can be accomplished in a variety of ways, including the use of ordered arrays, arrays of queues (one for each priority level), or heaps. As the heap option is by far the most efficient for a large number of items, we'll focus on this implementation.
Heaps are special kinds of binary trees. To be specific, a heap is a complete binary tree in heap order. We define these two new terms (and others) below.
A complete binary tree is one in which all the levels present are completely filled, with the possible exception of the lowest one, which is filled on the left to some point, and then empty from that point to the right. An example is shown below:
It should not be surprising, given similar arguments for binary search trees, that the height of a complete tree of size $n$ is $\lfloor \log_2 n \rfloor$, and increases only when $n$ is a power of $2$.
Here's the really cool thing -- unlike binary search trees, which we implemented with nodes that held references to other nodes -- we can represent complete binary trees using only an array. There is no need for links of any kind!
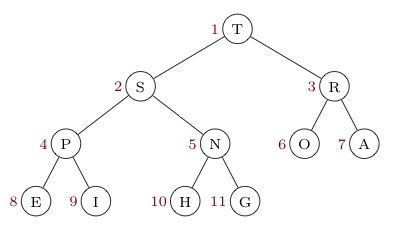
The trick is to store the items in the tree in an array in level-order (i.e., from top down, and left to right -- like reading a page of a book). An example is shown below -- note the numbers in brown to the left of each node, which indicate the position in the array where that item is stored.
Similar to binary search trees, we typically store key-value pairs in the nodes, where the key have some total order imposed upon them. If we are to use the related heap as a priority queue, it will be important to decide if priority should given to smaller or larger keys. If priority is given to smaller keys, we call the related heap a min heap. If priority is given instead to larger keys, we call this a max heap.
For example, if an operating system keeps a priority queue of jobs it needs to run, and wants to give priority to jobs that will finish quickly, then it can use the estimated finishing times as keys in a min heap. Whereas, various jobs worked on by a contractor might be prioritized by the amount of profit each is expected to produce, with jobs resulting in more profit being prioritized over those with less. The contractor should then use the expected profits as keys in a max heap.
A max heap is in heap order if every parent key is greater than or equal to the keys of its children. A min heap is similarly in heap order if every parent key is less than or equal to the keys of its children. In both cases then, the item at the top of the tree always represents the item with the highest priority item. This is the key feature that lets us use a heap as a priority queue -- as the highest priority item in a tree in heap order is always in the same place and easily removed. Note that if the above tree was to be used as a priority queue where letters closer to the end of the alphabet had priority over letters closer to the beginning, then it is in heap order and functions as a max heap. Notice also, as expected, the letter above that is closest to the end of the alphabet, $T$, is on top.
One should notice one more interesting thing about the heap pictured above. Look at the array representation -- notice the absence of anything stored at index $0$. Why would we leave this one element of the array unfilled, you ask? Remember, we said that we could represent heaps with arrays -- that we needed no links of any kind. That said, we still need to be able to navigate the underlying tree. That is to say, we need to be able to jump from looking at the key of any one node to looking at the key of either its parent or one of its children. Not placing an item at index $0$ allows us to do that.
Look at the index of $H$ above, which is $10$. What's the index of its parent, $N$? Notice that this index, $5$, is exactly half of the index for $10$. What about $N$'s parent, $S$? Here too, we simply divide $5$ by two -- throwing away the remainder if there is one. This works for every parent-child pair -- if some child is at index $n$, then its parent is at index $n/2$, where the division involved is "integer division" and consequently ignores remainders. (Take a moment and convince yourself of this, by looking at other nodes in the tree above.)
Getting from any parent to its children is just as easy. Notice if the parent is at index $n$, the left child is always at index $2n$ and the right child is at index $(2n+1)$. Further, at the bit-level, multiplying or dividing by 2 and adding 1 are some of the simplest (and fastest) operations one can do on a computer. Surely sacrificing the one element at index $0$ is worth this super fast means to navigate from one node of a heap to another!
Now, returning to the use of a heap as a priority queue -- recall that we earlier said the item of highest priority in such a heap would always be located at the top of the tree. This is true when the tree is in heap order -- but the act of dequeuing (removing) the highest priority item from the heap will likely break that heap order, at least temporarily. So how do we restore heap order to a heap once its topmost element has been removed?
We'll address that in the next section...