Merge Sort

In a merge sort, the basic idea is to:

Divide an array into two halves
Sort each half
Merge the two sorted halves into a sorted array

Input            M E R G E S O R T E X A M P L E
Sort Left Half   E E G M O R R S
Sort Right Half                  A E E L M P T X
Merge Results    A E E E E G L M M O P R R S T X

Being "smaller" lists, the sorting of the left and right halves are easily done recursively, until they become lists of only one element -- which are trivially already sorted.

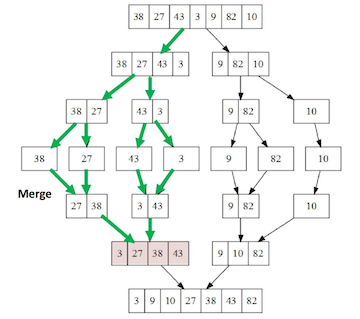
The below diagram shows the recursive breakdown of a list of integers (up to the center row) and merging together of various pairs of smaller lists created into the final sorted array. The green arrows highlight the work done just to sort the first half of the original list (shown in pink). Be careful about interpreting the below picture, however. Unless one is working in an environment where different actions can happen simultaneously, the steps below happen in a certain sequence. Often, we choose to proceed with the various "left halves" before working on their corresponding "right halves". Below, this means that all the actions corresponding to the green arrows happen BEFORE the actions corresponding to the black arrows. Even within the green arrow actions, the merge of 38 and 27 between the fourth and fifth rows, for example, happens before the array [43,3] gets examined (in the 3rd row).

But how do we "merge" two ordered subarrays into a longer ordered array?

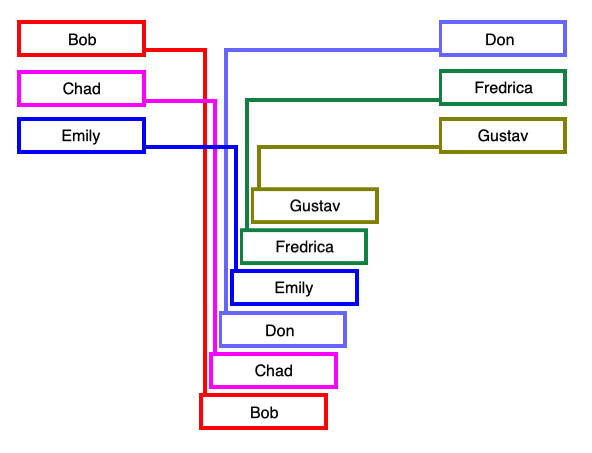
Imagine a teacher has two stacks of papers, each already alphabetized by the student names that appear at the top of the papers, and now they need to be merged together into a single alphabetized stack. The first stack has a paper by Bob on the top, while the second has a paper by Don on top. Which paper needs to be the first in the merged stack? "B" comes before "D", so we take Bob's paper off the first stack and place it face down on the table, as the first paper of our merged stack. This reveals Chad's paper, now sitting on the top of the first stack. Which paper should be next in your merged stack -- Chad's or Don's? Well "C" comes before "D", so you take Chad's paper off of the first stack, flip it over, and place it on top of Bob's. This reveals a paper by Emily, now at the top of the first stack. Which do you choose to put face down on the table now -- Emily's or Don's? Well, "D" comes before "E", so this time, take Don's paper off the second stack, flip it over ond put it on top of Chad's. This reveals Frederica's paper, etc. That's really about all there is to it -- you just keep picking papers to add to the merged pile in this way until one of your two stacks runs out, at which point you can flip over the entire remaining stack, and add it to your merged stack.

The important thing about the process described above is that we need some table space to put the two sorted half-stacks as we merge them into a single sorted stack. Similarly, when we implement the same algorithm in code to merge two sub-arrays, we'll want to have access to a second auxiliary array large enough to hold these two sub-arrays. If we create an array as long as the one we are attempting to sort at the very beginning of the entire process (i.e., before any recursive calls have happened), we will only have to create this extra space once. For each merge needed, we just copy all of the elements from the two sub-arrays we are merging to the auxiliary array as a temporary place to hold them, and then merge them back into the same positions in the original array, but in the proper order this time.

Implementation

To see how a single merge is accomplished in code, let us assume the original array to be sorted is held in an instance variable a[] and we have also defined an auxiliary array instance variable aux[]. We further suppose we have the standard "helper" instance method less(v,w) for comparing the Comparable items v and w.

It will be nice if the merge() method we are to write can be invoked on whatever parts of the original array we need over the course of the entire sorting algorithm. As such, let us assume we are trying to merge two sections of the array that span from index lo to index hi, where one extends from index lo to index mid, and the other extends from index mid+1 to index hi, where mid=(lo+hi)/2. Consequently, we pass lo, mid, and hi to the method as parameters. Of course, we also assume these two sections have already been sorted by earlier (recursive) calls to this same method..

First, we copy these elements from the original array to the auxiliary array, and then we do the following:

Start by examining the first elements (i.e., the smallest) of each half. Let us keep track of the positions of the elements being compared in the first and second halves with variables i and j, respectively. Initially, these are then i = lo and j = mid+1
We compare and copy the smaller element (aux[i] or aux[j]) to a[k] where k=lo, initially.
We increment the index (i or j) associated with the half from which we copied, and also increment k
If we reach the end of either half, we copy the remaining elements from the other half, incrementing indices as necessary

Here's an implementation in Java:

private void merge(int lo, int mid, int hi) {

   // make a copy in the auxiliary array...
   for (int k = lo; k <= hi; k++) {
       aux[k] = a[k];
   }
        
   // merge back to original array...
   int i = lo;
   int j = mid + 1;
   for (int k = lo; k <= hi; k++) {
     if (i > mid)                   a[k] = aux[j++]; // left half exhausted, copy from right 
     else if (j > hi)               a[k] = aux[i++]; // right half exhausted, copy from left
     else if (less(aux[j],aux[i]))  a[k] = aux[j++];  
     else                           a[k] = aux[i++];
   }
}

Once we have the merge method written, implementing the rest of the algorithm on the elements from lo to hi is easy. We check to see if we are in the base case for the recursion first (i.e., a subarray of one element, where hi $\le$ lo). If we are, we're done. If not, we need to calculate the value of mid, make our two recursive calls to sort the left and right halves, and then merge these two halves together:

private void mergeSort(int lo, int hi) {

    if (hi <= lo) return;           // are we in the base case? 

    int mid = lo + (hi - lo) / 2;
    
    mergeSort(lo, mid);             // sort left half
    mergeSort(mid+1, hi);           // sort right half

    merge(lo, mid, hi);             // merge the two sorted halves together
}

Improvements

The merge sort is a beautiful and incredibly fast, divide-and-conquer recursive algorithm for sorting. That said, there are still things we can tweak to make it run even faster:

Use insertion sort for small subarrays. Merge sort shines when applied to large lists, but simply has too much in the way of overhead costs relative to the actual sorting it accomplishes when applied to tiny subarrays. On the other hand, insertion sorts are able to sort tiny subarrays quickly, but slow down to a crawl for large lists. Why not have the best of both worlds? Before calculating mid and making the recursive calls to your sorting method, first check to see if hi is less than low plus some cutoff value (typically $\approx 10$). If it is -- use insertion sort for this span in the array and move on with life. If not, let the merge sort do its thing.
Check to see if merging is necessary. Ever look at a new deck of cards that has been poorly shuffled? There are often long spans of cards that are still in perfect order. This crops up in real-life applications all the time. We can easily avoid the high cost of blindly merging a bunch of things that are already in order, however. Suppose your two sub-arrays to be merged look like this: $$\begin{array}{|c|c|c|c|c|c|} \scriptsize{\texttt{lo}} & & & & & & &\scriptsize{\texttt{mid}}&\scriptsize{\texttt{mid+1}}& & & & & & &\scriptsize{\texttt{hi}}\\\hline \color{blue}A & \color{blue}B & \color{blue}D & \color{blue}E & \color{blue}G & \color{blue}H & \color{blue}I & \color{blue}K & \color{green}M & \color{green}P & \color{green}Q & \color{green}S & \color{green}U & \color{green}W & \color{green}Y & \color{green}Z\\\hline \end{array} $$

sort()

mid+1

mid

Eliminate the copy to the auxiliary array. Imagine strumming the strings of a guitar always in the top-to-bottom direction versus strumming the strings first from top-to-bottom, then back from the bottom to the top, then top-to-bottom again, etc. Reversing the direction each time should double the speed of your strumming, as all that time getting your hand back to the top string for another strum is not wasted.

The same principle can be applied to the merge sort. Switch the role of the initial and auxiliary array in each recursive call, and avoid all that extra copying used only to always merge in the same direction (i.e., back into the initial array)! Assuming we initialize aux[] to a[] before the recursive calls, here's how to do this quickly in code:

private void merge(Item[] a, Item[] aux, int lo, int mid, int hi) {
  int i = lo;
  int j = mid+1;
  for (int k = lo; k <= hi; k++) {
    if (i > mid)                aux[k] = a[j++];
    else if (j > hi)            aux[k] = a[i++];
    else if (less(a[j], a[i]))  aux[k] = a[j++];  // <-- notice we always merge from
    else                        aux[k] = a[i++];  //     a[] to aux[] here;
  }
}

private void sort(Item[] a, Item[] aux, int lo, int hi) {
  if (hi <= lo) return;  
  int mid = lo + (hi - lo) / 2;

  sort (aux, a, lo, mid);        //<-- note in the two calls to sort(), aux[] comes
  sort (aux, a, mid+1, hi);      //    before a[], but in sort's method signature and
  merge(a, aux, lo, mid, hi);  } //    in merge(), they are reversed.  this is how
                                 //    aux[] and a[] get repeatedly switched.